垂心 – ベクトル OH |位置ベクトルで表示する【図形の証明も考察】
" 垂心 – ベクトル OH"について、位置ベクトルで表示することについて解説をしています。
垂心については、各頂点から向かい合う辺に下した三本の垂線が、１点のみで交わることの証明を平面図形の単元で学習します。
この図形的な内容に、さらにベクトルの内容を加えて、垂心の位置ベクトル表示が得られます。
まずは、三本の垂線が１点のみで交わることを証明します。
垂心についての平面図形の証明が完成すると、ベクトルについての理論を使います。
記事の後半では、具体的な数値を用いて、垂心を位置ベクトルで表します。
垂心 :平面図形の証明
【定理】
三角形OAB について、点 O, A, B から、それぞれの対辺に引いた垂線の足を C, D, E とする。
このとき、直線OC, AD, BE は１点のみで交わる。
＜証明＞
直線OC と直線AD は平行でないので、１点のみで交わります。
その交点を H と置くことにします。
直線AO に平行な補助線を引きます。
同じく、直線BA に平行な補助線と直線OB に平行な補助線を引きます。
そして、これらの平行に引いた直線の交点たちを点 P, Q, R とします。
ここまでの内容を図にまとめます。
図で可視化
図の赤色で描いている線が、平行に引いた補助線です。
証明すべき内容は、直線BE も、点 H を通るということです。
ここで、平行四辺形についての性質を使い、既に学習している外接円の内容へと議論を帰着させます。
四角形APBO、ABQO は、向い合う二組の辺が、それぞれ平行なので、平行四辺形となっています。
平行四辺形の向かい合う辺の長さは等しいため、次の等式が得られます。
OA = BP, OA = QB です。
このため、
点 B は、三角形PQR の辺PQ の中点となっています。
さらに、仮定から、
BE ⊥ OA で、
直線AO と PQ が平行より、
EB ⊥ PQ です。
よって、直線BE は、辺PQ の垂直二等分線となっています。
四角形OAPB, OQAB も同様に平行四辺形となっています。
そのため、同様の考察で、
直線AD が辺PR の垂直二等分線ということが分かります。
さらに、
四角形ABQO, ABOR も平行四辺形となっています。
同様にして、
直線OC は辺QR の垂直二等分線となっています。
三角形PQR について、各辺の垂直二等分線は、すべて外接円の中心の１点のみで交わります。
そのため、直線OC, AD, BE は１点のみで交わるということが示せました。【証明完了】
先ほど示した内容ですが、三角形PQR の外接円の中心である外心が、もとの三角形OAB の垂心です。
※ 外接円という記事で、三角形の各辺の垂直二等分線が、すべて外接円の中心の１点のみで交わることを幾何的に証明しています。
ここまでの平面図形の内容に、チェバの定理の内容を加味して考察を進めます。
垂心 – 位置ベクトル :ここから線分比
三角形OAB について、点 O, A, B から、それぞれの対辺に引いた垂線の足を C, D, E とし、直線OC, AD, BE は１点が垂心 H でした。
そうすると、チェバの定理から、
AC/CB × BD/DO × OE/EA = 1 となっています。
このチェバの定理の結論が成立している分点比について、三角形の内部で交わっている三本の線の交点 H について、次の線分比となることが分かっています。
OH : HC =
(AC+CB) : BD …★となります。
この内容から、点 H を位置ベクトル表示することができます。
※ チェバの定理の逆という記事で、具体的に位置ベクトルを用いて表すことを解説しています。
これで、垂心を位置ベクトルで表示する理論が得られました。
このリンク先の記事の内容を少し修正して、点 O を位置ベクトルの基準として、具体的な数字を使った例で、垂心の位置ベクトル表示を行います。
具体例で練習
【練習問題】
三角形OAB について、
OA = 5, OB = 6,
AB = 7 とします。
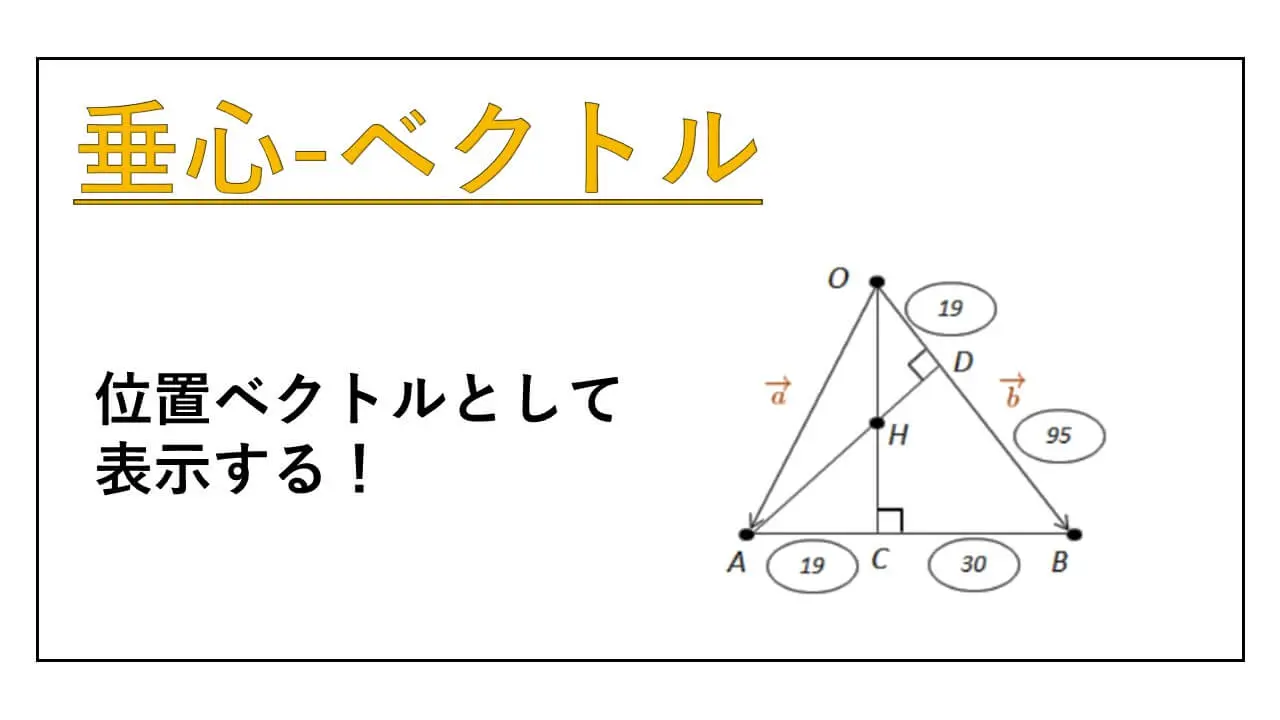
このとき、ベクトルOA を a、ベクトルOB を b として、三角形OAB の垂心 H を表す位置ベクトル h を a と b を用いて表示してください。
下の図の内容となっています。
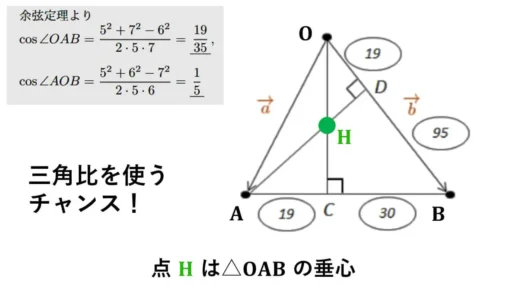
余弦定理より、
cos∠OAB = 19/35,
cos∠AOB = 1/5 という値が得られます。
直角三角形OAC, ADO について、三角比を使うチャンスです。
AC = OA × cos∠OAB
= 5 × 19/35 = 19/7 です。
そのため、
CB = AB － AC
= 7 － 19/7 = 30/7 です。
これで、
AC : CB = 19/7 : 30/7
= 19 : 30 と線分比が得られました。
今度は直角三角形OAD について三角比を考えます。
OD = OA × cos∠AOB
= 5 × 1/5 = 1 です。
そのため、
BD = OB － OD
= 6 － 1 = 5 です。
これで、
BD : DO = 5 : 1 です。
ここで、油断しないように注意です。
先ほどの★を使うのですが、注意点があります。
連比のときの数値に注意
OH : HC =
(AC+CB) : BD …★
これを使うときに、線分比の比を表している数値には注意が必要です。
チェバの定理の逆に関連して、交わった１点の位置ベクトル表示を求めるときに、各辺について連比となっているという前提で位置ベクトル表示を導いています。
そのため、
AC : BC を表す AC に関する比の数値と、BD : DO を表す DO に関する比の数値を同じ値に揃えておくことが必要になります。
ここを揃えておかないと、答えに誤りが出るときがあるので注意です。
AC : CB = 19 : 30,
BD : DO = 5 : 1 となっていました。
AC についての比が 19 で、DO についての比が 1 と異なる値になっています。
そのため、比の値を揃えてから、結論を導きます。
19 倍して、
BD : DO = 95 : 19 とします。
このように比を表している数値を揃えておいてから、★の内容を使います。
OH : HC =
(CB+BD) : BD
= (19+30) : 95
= 49 : 95 となります。
これで、49/144 にベクトルOC を縮小するとベクトルOH となることが分かりました。
ベクトルOC を分点公式を用いて求めます。
(30/49)a+(19/49)b となります。
つまり、これを 49/144 という実数でスカラー倍すると、求める h です。
h = (30/144)a+(19/144)b です。
連比が絡むというところが落とし穴になるという問題でした。
チェバの定理の逆が成立してから、三角形の内部で交わった１点を位置ベクトル表示するときには、連比に注意です。
関連する記事について
平面図形とベクトルの内容をトレーニングするには、三角形の五心を位置ベクトルで表示することが良い練習になります。
垂心に関連して、これらの記事の内容を投稿しています。
図形的な性質と、ベクトルを関連させて理解しておくと、数学や物理の表現力が磨かれるかと思います。
先ほどの練習問題で、敢えて連比によって発生するであろう混乱について述べました。
やはり、表面的な公式の暗記で、数だけを当てはめるということだけをすると、まちがってしまうような出題が予想されます。
これら五心の内容や、チャバの定理の逆から三角形の内部で交わる１点の位置ベクトル表示について、どうやって導いているのかを正確に理解し、いつでも自力で導けるくらいにまでベクトルに慣れておくことが重要かと思います。
それでは、これで今回のタロウ岩井の記事を終了します。
読んで頂き、ありがとうございました。