ラウールの法則 | 蒸気圧降下について簡単にわかりやすく解説
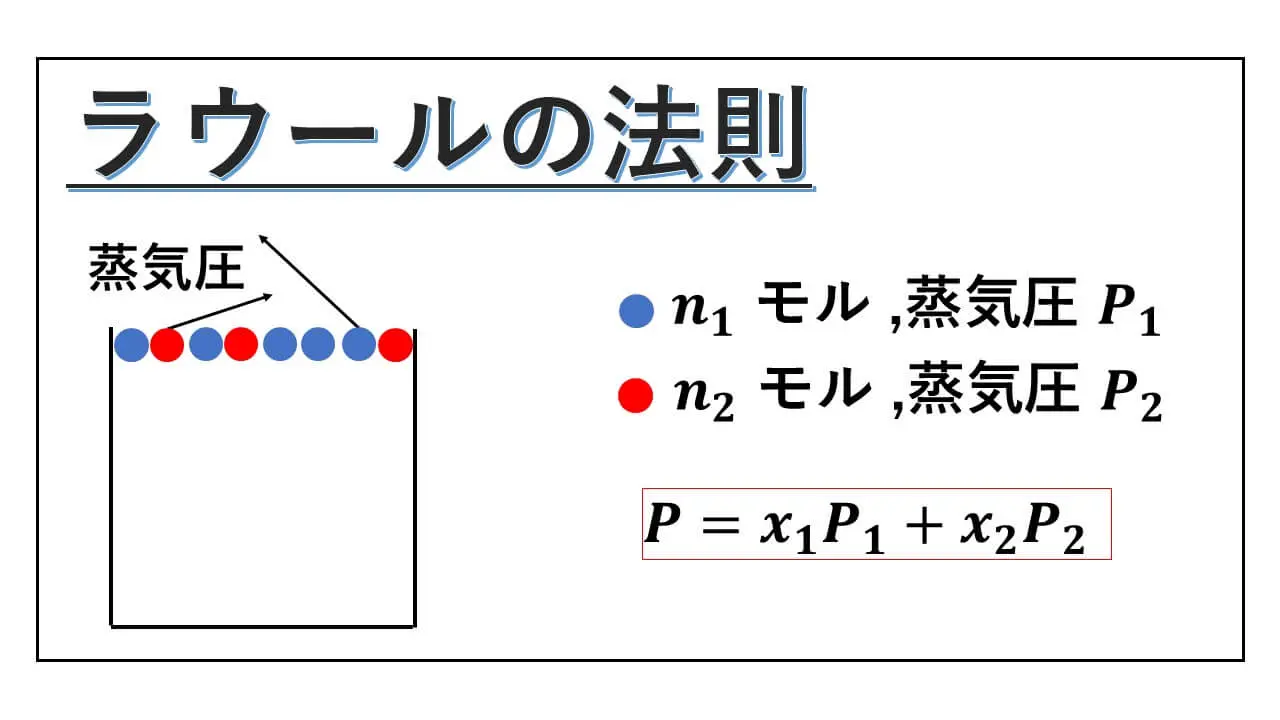
" ラウールの法則 “は、複数の純溶媒を混ぜ合わせたときに、液体表面からの蒸気圧がどうなるのかを示す内容になっています。
ラウールの法則が成立するために、細かい条件があるのですが、学習し始めの分かりやすさを狙って、このあたりはざっくりとしたものに留めています。
理科の用語の意味を着実に押さえておくことと、使われている数学の文字記号が示す内容を正しく把握することができると、すぐに学習し始めの練習問題を正解できる単元内容になります。
細かい難しい内容にとらわれ過ぎずに、まずは典型的な内容を理解することに専念しておくと、気分良く高校の化学の学習を進めることができるかと思います。
ラウールの法則 :式が表す内容を簡単にわかりやすく
ラウールの法則が成立するためには、溶液が十分に希薄であるといった条件があります。
中には混ぜ合わせただけで発熱するといった溶液どうしのケースなどもあり、ラウールの法則が成立しないケースも起こり得ます。
ただ、高校の化学の学習をし始めたときに、スムーズに学習が進められるように、十分に希薄な理想溶液という前提で、あくまで式が示している内容を把握することを主眼に説明を進めています。
これから純溶媒という言葉をよく使いますが、これは液体に何も溶かしていないものと思っておいてください。
例えば、純溶媒として、ベンゼンを例として使っています。
ベンゼンという液体には何も溶かしていません。
このベンゼンの液体の表面からは、蒸気圧が出ています。
溶媒の粒子が気体の粒子として空中へと飛び出し、蒸気圧が生じています。
このベンゼンだけのときの蒸気圧に対して、例えばベンゼンにトルエンという他の純溶媒を混ぜた後の蒸気圧がどうなるのかということを考えます。
ベンゼンだけのときの蒸気圧、トルエンだけのときの蒸気圧、そして混ぜ合わせた後の蒸気圧について述べているのがラウールの法則です。
具体的な数字を使うと、気圧1.1×105Paというように複雑な数字になるので、ここは数学の文章問題の要領で文字を使って、一般的に成立する内容を押さえるようにします。
公式に使われている文字が表す理科の内容と、数学（算数）の内容を適切に把握することが大切になります。
ラウールの法則の式
純溶媒１がn1モルあり、その蒸気圧がP1気圧だとします。
また純溶媒２がn2モルあり、その蒸気圧がP2気圧だとします。
これら２つの純溶媒を混ぜ合わせた後の液体表面からの気圧 P は、次のようになります。
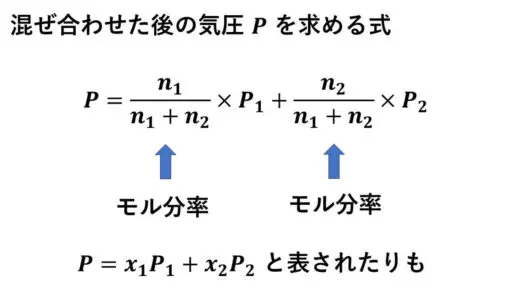
ここで、まずモル分率という理科の言葉と数学（算数）の割合の内容を把握しておきます。
n1モルとn2モルを混ぜ合わせると、全体は(n1+n2)モルになります。
この全体において純溶媒１のn1モルが占める割合が、純溶媒１のモル分率です。
文字を使った式で表すと、
n1/(n1+n2) が混ぜ合わせた後に純溶媒１が占める物質量の割合になります。
同じく、
n2/(n1+n2) が混ぜ合わせた後に純溶媒２が占める物質量の割合です。
両方の割合を合計すると、
(n1+n2)/(n1+n2) = 1 と、百パーセントを表す割合１となっています。
これらモル分率との積を使って、混ぜ合わせた後の蒸気圧についての等式が得られるというのがラウールの法則です。
数学でもよく使う手ですが、他の文字で置くということもあります。
純溶媒１のモル分率をx1、純溶媒２のモル分率をx2と置くことで、モル分率をベースとした式で表されることもあります。
それが、
P = x1P1+x2P2 という式になります。
理系の方だと、ベクトルの分点公式みたいな式なので、数学を学習するときの要領で学習を進められるかと思います。
化学を学習しつつ、数学の気分も良く学習を進められると、良い勉強のサイクルができます。
【練習問題】
ベンゼン 1 モルの蒸気圧がP1、トルエン 4 モルの蒸気圧がP2だとします。
このとき、これら２つの純溶媒を混ぜ合わせた後の気圧 P を、P1と P2 を用いて表してください。
ラウールの法則を使うために、それぞれのモル分率を求めておきます。
P = x1P1+x2P2 という式を使うには、それぞれのモル分率を自分で計算しておかなければなりません。
そのため、n1 = 1 モル、n2 = 4 モルという状態から、
n1/(n1+n2) と n2/(n1+n2) というモル分率を計算します。
今、n1+n2 = 1+4 = 5 なので、
1/5 = 0.2 がベンゼンのモル分率です。
トルエンのモル分率は、
4/5 = 0.8 です。
ラウールの法則の式の x1 が0.2で、x2 が0.8と値が分かったので、混ぜ合わせた後の気圧 P を表すことができます。
すなわち、
P = 0.2P1+0.8P2 となります。
アボガドロ定数や原子量-分子量の単元で学習したモルの計算が絡むので、基礎からしっかりと学習をしておくと、こういったところで効いてきます。
x1やx2というモル分率まで押さえたので、参考までに３種類以上の純溶媒を混ぜ合わせたときについてのラウールの法則の式も述べておきます。
３種類以上の純溶媒について
【ラウールの法則】
純溶媒 1 の蒸気圧がp1でモル分率がx1,
純溶媒 2 の蒸気圧がp2でモル分率がx2,
・・・
純溶媒 n の蒸気圧がpnでモル分率がxn だとする。
このとき、これら n 種類の純溶媒を全て混ぜ合わせた後の蒸気圧 P は、
P = x1P1+x2P2+…+xnPn である。
数学Bで学習するシグマ記号の意味を知っていると、次のように等式を表すこともできます。
つまり、
P = Σk=1 xkPk です。
k 番目の純溶媒が akモルだとすると、k 番目のモル分率は次です。
すなわち、
ak/(a1+a2+…+an) が k 番目の純溶媒のモル分率 xk の値です。
このように、理系の方だと、理科を学習しながら数学の内容にも触れることができます。
１つの科目を学習しながら、数学の復習にもなってくれるので、こうなると勉強の効率が上がります。
ここからは、もう一度、2 種類の純溶媒のときの内容に話を戻し、不揮発性物質を溶かした溶液についての蒸気圧降下について説明します。
蒸気圧降下と不揮発性物質
１つの純溶媒に不揮発性の溶質を溶かすと、純溶媒のときに比べて蒸気圧が低下します。
これが蒸気圧降下です。
不揮発性の物質は蒸気にならない物質と思ってください。
先ほど、ラウールの法則を純溶媒１と純溶媒２のときについて述べましたが、今度は純溶媒２のかわりに不揮発性物質を考えるわけです。
不揮発性なので蒸気圧P2の値は 0 です。
0 との掛け算の値が 0 となり、0 を足しても値が変わらないという数学の内容を踏まえて、ラウールの法則から蒸気圧降下についての式を考えます。
【蒸気圧降下の式】
純溶媒の n1 モルの蒸気圧が P だとする。
ただし、n1 > 0 である。
この純溶媒に不揮発性の物質 n2 モルを溶かしてできた十分に希薄な溶液の蒸気圧を P’ とする。
このとき、
P’ = n1/(n1+n2) × P である。
※ n1/(n1+n2) というモル分率を x と置くと、
P’ = xP です。
＜証明＞
溶液の表面において、不揮発性の物質からの蒸気圧は、
n2/(n1+n2) × 0 = 0 です。
純溶媒の n1 モルの蒸気圧が P だったので、こちらからの蒸気圧は、
n1/(n1+n2) × P です。
ゆえに、不揮発性の物質を溶かした後の蒸気圧 P’ について、ラウールの法則より、
P’ = n1/(n1+n2) × P+0
= n1/(n1+n2) × P です。
n1/(n1+n2) というモル分率を x と置くと、
P’ = xP です。
これで、【証明完了】です。
不揮発性の物質を溶かしていないときは、n2が 0 なので、
P’ = n1/(n1+0) × P
= 1×P = P と純溶媒のときの蒸気圧のままになっています。
確実に不揮発性の物質を溶かした場合だと、
n2 > 0 なので、
0 < n1/(n1+n2)
< n1/n1 = 1 です。
そのため、モル分率 x は、
0 < x < 1 なので、両辺に P を掛けると、
0 < xP < P です。
P’ = xP なので、
P’ < P と、不揮発性の物質を溶かした後の蒸気圧が低下した値となっています。
さらに、蒸気圧降下度の式について述べておきます。
蒸気圧降下度の式
不揮発性の物質を溶かす前の蒸気圧 P から、溶かした後の低下した蒸気圧 P’ を引いた差をΔP と表すことにします。
つまり、
ΔP = P－P’ の値を蒸気圧降下度といいます。
この値は、どれだけ蒸気圧が低下したのかを表しています。
P’ にラウールの法則の式から導いた先ほどの式を代入してみます。
ΔP = P－P’
= P－n1/(n1+n2) × P
= {1－n1/(n1+n2)} × P
= (n1+n2－n1)/(n1+n2) × P
= n2/(n1+n2) × P
これは、液体表面で不揮発性の物質のモル分率の分だけ、溶媒の粒子が蒸気となることを妨げられていることを表しているかのような式です。
この内容をモル分率の文字を使ってまとめておきます。
純溶媒の蒸気圧が P で、これに不揮発性の物質を溶かした後の蒸気圧を P’ とします。
溶かした後の溶液について、溶媒のモル分率が x で、不揮発性の物質のモル分率を y とします。
割合の関係から、
x+y = 1 となっています。
この１は溶液全体の百パーセントを表す割合の１です。
ラウールの法則から、
P’ = xP です。
そして、
蒸気圧降下度について、
ΔP = yP となっています。
P からP’ を引いた差もモル分率を用いて表されているということです。
今回は、数学の不等式の証明で扱われる内容を使いました。
1 より値が小さい正の実数を掛けると、積がもとの値よりも小さくなるという内容でした。
有機化学の計算についても、組成式-式量という記事を投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。