オイラー線 – 比 | EGとGHの比が1:2であることを示す【同一直線上の3点】
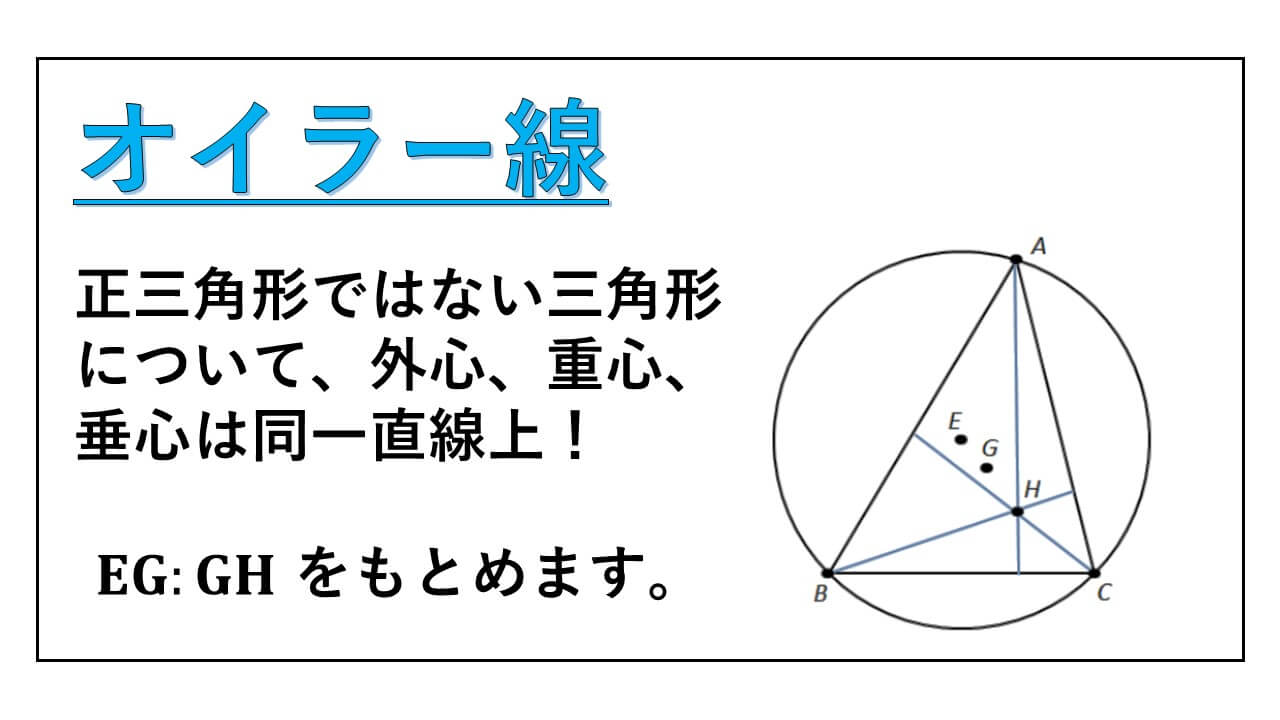
" オイラー線 “についての比を示しています。
正三角形ではない三角形が与えられたとき、その三角形の外心を E、重心を G、垂心を H とすると、これらの3点は同一直線上の点となっています。
そして、EG : GH = 1 : 2 です。
この内容を平面ベクトルについての基礎的な計算から導きます。
この記事では、正三角形ではない三角形ABC が与えられたとし、この三角形の外接円の中心を E と表すことにします。
やや作為的ですが、
EA+EB+EC というベクトルの終点を H と置きます。
まず、垂直なベクトルどうしの内積値が 0 となることを利用して、この H が、どういう点かということを考察します。
オイラー線 :点Hが何かを考える
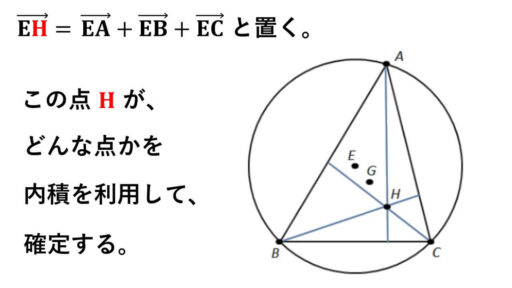
直線AH, BH, CH が、それぞれ対辺と垂直になっていることがベクトルの内積の計算から導かれます。
実際に、AH と BC の内積が 0 となることを示します。
始点を A とする式に書き換えます。
AH = EH-EA
= EB+EC となります。
よって、
EB・EC = EC・EB より、
AH・BC =
(EB+EC)(EB-EC) =
EB・EB-EC・EC・EC
= |EB|2-|EC|2
ここで、線分EB と線分EC は三角形ABC の外接円の半径なので、等しい長さになっています。
そのため、
AH・BC = |EB|-|EC| = 0 です。
ゆえに、直線AH と直線BC が垂直ということが分かりました。
これで、点 H が、どういった点であるのかが見えてきました。
三角形の各頂点から、それぞれの対辺に下した三本の垂線が交わる1点が垂心です。
そのため、あとは、直線BH と 直線CA が垂直で、直線CH と直線AB が垂直となっていることを示すと、点 H が三角形ABC の垂心ということになります。
これらについても、先ほどと同様の計算で確認することができます。
同様にして
EA, EB, EC は三角形ABC の外接円の半径なので、どの二つも等しい長さになっています。
そのため、
BH・CA
= (EH-EB)(EA-EC)
= (EA+EC)(EA-EC)
= |EA|2-|EC|2 = 0
つまり、BH ⊥ CA です。
また、
CH・AB
= (EH-EC)(EB-EA)
= (EB+EA)(EB-EA)
= |EB|-|EA| = 0
つまり、CH ⊥ AB となっています。
これで、点 H が三角形ABC の垂心となっていることが分かりました。
垂心の位置ベクトル表示については、リンク先の記事で解説をしています。
ここからは、三角形ABC の外心 E、重心 G、垂心 H が、同一直線上にあることを示します。
この3点を結んだ線を発見者のオイラーにちなんでオイラー線といいます。
オイラー線 – 比 :同一直線上
正三角形ではない三角形ABC の外心を E、重心を G とし、上で述べた点 H が垂心です。
EH = EA+EB+EC という関係を使って、3点 E, G, H が同一直線上にあることを示します。
GH = EH-EG
= EA+EB+EC-EG
= EA+EB+EC+0-EG…★
零ベクトルと加法を計算しても値が変わらないので、敢えて 0 を最後に加えました。
ここから、次の命題の内容を加味すると、議論が広がります。
【命題1】
三角形ABC の重心 G について、
GA+GB+GC = 0 である。
重心のベクトル表示より、
3AG = AB+AC ということから、結論が導けます。
GA+GB+GC =
-AG+(AB-AG)+(AC-AG)
= -3AG+AB+AC
= -(AB+AC)+AB+AC
= 0
これで、【命題1】が示せました。
この命題から、
-(GA+GB+GC) = 0 です。
先ほどの★の 0 を、この左辺で書き換えます。
すると、
GH = EA+EB+EC+0-EG
= (EA-GA)+(EB-GB)+(EC-GC)-EG
= (EA+AG)+(EB+BG)+(EC+CG)-EG
= 3EG-EG
= 2EG = -2GE
これで、三角形ABC が正三角形でないため、3点 E, G, H が、どの2つも異なる点なので、同一直線上にあることが示せました。
ベクトルGE を -2 でスカラー倍するとベクトルGH という状況になっています。
線分比も求まっています
今、示したベクトルの等式より、等しいベクトルの長さが等しいことから、次を得ます。
つまり、
|GH| = 2|GE| です。
|GE| = |EG| なので、
|EG| : |GH| = 1 : 2 です。
これは、
点 G が線分EH を
1 : 2 に内分しているということを意味しています。
ベクトルを使わない形で記すと、
EG : GH = 1 : 2 ということです。
これで、オイラー線についての比も求まりました。
ここまで、三角形ABC が正三角形でないので、外心、重心、垂心が、どの二つも一致していないという平面図形の単元で学習する事実に基づいて議論を進めました。
最後に、平面図形の復習に、このことを証明しておきます。
対偶命題を使うことで、中学の合同や相似の単元で練習した図形の証明の内容で示すことができます。
オイラー線 :基礎的な図形の性質
【命題2】
三角形ABC が与えられたとする。
このとき、
三角形ABC の外心と重心が点 G で一致しているならば、三角形ABC は正三角形である。
<証明>
三角形ABC の外心と重心が点 G で一致しているということから、各辺の垂直二等分線が中線となっているということです。
そのため、辺 BC の中点を P とすると、
AP ⊥ BC となっています。
線分BC の垂直二等分線上の点は、端点 B, C から等しい距離にあります。
よって、
AB = AC …①
また、CA の中点を Q とすると、
BQ ⊥ CA です。
そのため、線分CA の端点 C, A から等しい距離にある点全体が直線BQ です。
よって、BC = BA …②
①と②より、
AB = BC = AC となり、三辺の長さが全て等しいことから、三角形ABC は正三角形となっています。【証明完了】
この【命題2】の対偶も真なので、
三角形ABC が正三角形でなければ、その外心と重心は一致していないということになります。
今度は、正三角形でなければ、重心と垂心が一致しないということを示します。
対偶命題を示す
【命題3】
三角形ABC が与えられたとする。
このとき、
三角形ABC の重心と垂心が点 G において一致しているならば、三角形ABC は正三角形である。
<証明>
AG ⊥ BC となっています。
G が重心なので、AG と BC の交点は、BC の中点となっています。
BC の中点を P と置くと、
三角形ABM と三角形ACM は合同となっています。
そのため、AB = AC です。
BG ⊥ CA より、
同様にして、
BC = BA です。
これで、AB = BC = AC より、三角形ABC は正三角形です。【証明完了】
【命題3】の対偶も真だから、
三角形ABC が正三角形でなければ、その重心と垂心は一致していないということになります。
残りは、三角形ABC が正三角形でなければ、外心と垂心が一致していないということを示すことになります。
既に示した議論に帰着する
【命題4】
三角形ABC が与えられたとする。
このとき、
三角形ABC の外心と垂心が点 H で一致しているならば、三角形ABC は正三角形である。
<証明>
直線AH, BH, CH と、それぞれの対辺BC, CA, AB との交点を P, Q, R と置きます。
垂心の定義から、
HP ⊥ BC, HQ ⊥ CA,
HR ⊥ AB となっています。
点 H は三角形ABC の外心でもあり、外心から三辺に下した垂線の足は、それぞれの辺の中点となっています。
そのため、点 P, Q, R は、それぞれ辺 BC, CA, AB の中点です。
よって、AP, BQ, CR は、三角形ABC の中線です。
これは、点 H が三角形ABC の重心ということになります。
よって、三角形ABC の外心と重心が一致していることから、【命題2】より、三角形ABC は、正三角形です。【証明完了】
これで、真である命題の対偶も真なので、三角形ABC が正三角形でなければ、外心と垂心が一致していないということが示せました。
これらの平面図形の内容を使って、上でオイラー線のことを述べました。
正三角形だと、外心、重心、垂心が全て一致し、線ではなく1点となってしまっています。
【関連する記事】
外接円という記事で、三角形の各辺の垂直二等分線が外心という1点で交わっているということを図形的に解説しています。
内心-外心という記事では、それらの点を位置ベクトルで表示することについて解説をしています。
それでは、これで今回のタロウ岩井の記事を終了します。
読んで頂き、ありがとうございました。