曲線の長さ – 導出 | 定義からの積分イメージ【アステロイドで練習】

" 曲線の長さ “の公式を定義から" 導出 “するときに、微小変化からの積分イメージを解説しています。
微小な時間変化に伴う点の移動した道のりを蓄積するところが、まさに積分の表すイメージにぴったりです。
また、アステロイド曲線という有名な曲線を題材にして、曲線の長さを導いた公式を使って求める実践練習としての内容も述べています。
高校数学IIIの発展内容になりますが、大学のベクトル解析への布石にもなりつつ、高校内容の良い考察の練習になるかと思います。
では、曲線の長さの定義と公式の導出から解説します。
微小な時間変化に伴る内容なので、微分の内容も出てきます。
まず準備として、時刻 t という実数に対して、xy平面上の座標を対応させるベクトル値関数について述べておきます。
曲線の長さ – 導出 :定義が示すイメージ
【ベクトル値関数】
xy座標平面上を移動する点 P について、
時刻 t(t は実数) に対し、点 P のいる位置の座標を対応させる関数を P(t) とする。
すなわち、
t における P の位置が、
x = f(t), y = g(t) のとき、
P(t) = (f(t), g(t)) とする。
※ ブログ加速度ベクトルより
これで、実数 t に対して、(0, 0) という原点を始点とする平面ベクトルを対応させる関数が定義できました。
ここから、定数 a, b について、
t = a のときに点 P がいた位置である点 A から、
t = b のときに点 P がいた位置である点 B までに点 P が進む道のりを定義することを考えます。
この点 P が動いた道のりが、点 A から点 B までを結ぶ曲線の長さというわけです。
※ 点 A から点 B までの間を点 P が直線で移動したときにも使える内容となっています。
P(t) = (f(t), g(t))(ただし a ≦ t ≦ b)が、
時刻 t における点 P の位置を示す座標となっています。
実数 t に対して、
P(t) という座標を対応させる関数で、
値域が平面ベクトルになっているからベクトル値関数です。
この関数と微小な経過時間に対して、微分からアプローチします。
微小変化ゆえのショートカット
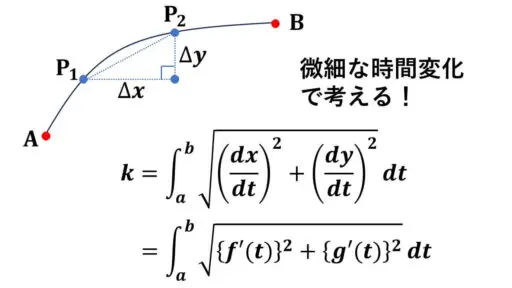
時刻 t のおける点 P の位置が、
x = f(t), y = g(t) となっていました。
ただし、f(t) も g(t) も t で微分可能という設定で、これから議論を進めます。
そこで、わずかな時間経過 Δt > 0 の間に点 P が図の P1 の位置から P2 の位置まで進むことを考えます。
曲線上を移動する点 P なので、実際は点 P1 から点 P2 への道のりは曲線となっています。
しかし、Δt が微小なため、点 P が点 P1 から点 P2 へコーナーをショートカットして図で青で示した直線で移動したとイメージします。
微小な時間経過 Δt の間に点 P の x 座標は Δx 変化し、点 P の y 座標が Δy だけ変化したことになります。
点 P が直線上を最短でショートカットしたことにより、時間経過 Δt の間に点 P の進む道のりが三平方の定理を使って表すことができます。
このショートカットした点 P の進む道のりを Δk と置くことにします。
すると、
|Δk| = {(Δx)2+(Δy)2}1/2 となります。
ここで、Δt ですが、時間を巻き戻すということも考えたいので、進んだ道のり Δk に絶対値をつけておきました。
時間を巻き戻すと、進んだ道のりが減少するため、その際は Δk がマイナスの値となります。
ただ、この絶対値は Δt が分母にくると外すことができます。
微小時間 Δt が正のときは、
点 P が少しだけれども進むので、Δk の値はプラスです。
Δt が負のときは、
点 P が進む道のりが巻き戻されるので、Δk の値はマイナスです。
つまり、Δt と Δk は同符号です。
そのため、中学一年の計算より、
Δk/Δt は正の値というわけです。
これで、絶対値の定義から、そのまま外して良いということになります。
すなわち、
Δk/Δt = |Δk/Δt|
= {(Δx/Δt)2+(Δy/Δt)2}1/2 です。
設定は Δt > 0 でした。
今、Δt を限りなく 0 に近づけるということを考えます。
Δt → 0 のとき、
Δk/Δt は dk/dt で、
Δx/Δt が dx/dt,
Δy/Δt が dy/dt となっています。
ゆえに、Δt → 0 のとき、
dk/dt = {(dx/dt)2+(dy/dt)2}1/2
= {(f'(t))2+(g'(t))2}1/2 となっています。
これで、微小時間 Δt に伴う微小な点 P の道のりを微分係数を使って表すことができました。
はじめ、t = a のとき点 P が点 A の位置にいて、
t = b のときに点 B の位置に点 P がいるということでした。
この点 A から点 B までの曲線の長さは、微小な dk/dt をつなぎ合わせたものと考えるのが自然です。
そこで、dk/dt をつなぎ合わせるというイメージを定積分で表現します。
導出 :長さを表す積分の表現力
a ≦ t ≦ b でした。
上で述べた dk/dt という微小な道のりをつなぎ合わせて、点 A から点 B までの曲線の長さ k を表現することを考えます。
こんなときは、定積分です。
k = ∫a (dk/dt) dt
= ∫a {(f'(t))2+(g'(t))2}1/2 dt
微小な道のりをつなぎ合わせて曲線の長さを定義するというわけです。
これで曲線の長さの公式を導出したわけですが、具体的な曲線について、公式を使うことを述べたいと思います。
理系の数学で有名な曲線を使って、その曲線の長さを公式で計算します。
微積の計算を着実に実行することが大切になります。
曲線の長さ :アステロイドで
【実践】
x = cos3t, y = sin3t (0 ≦ t ≦ π)
というアステロイド曲線の一部である曲線の長さを求めてください。
x = f(t) = cos3t,
y = g(t) = sin3t と時刻 t で媒介変数表示されていたと考えます。
P(t) = (f(t), g(t)) がアステロイド曲線上を動くとして、t が 0 から π までで進む道のりを公式を使って計算するというわけです。
導出した曲線の長さの公式を使いたいので、f'(t) と g'(t) を求めておくことが必要になります。
f'(t) = 3cos2t・(cos t)’
= -3cos2t sin t,
g'(t) = 3sin2t・(sin t)’
= 3sin2t cos t となります。
合成関数の微分が計算で絡みました。
これらを二乗してルートをつけるということをしたものを定積分します。
{f'(t)}2 = 9sin2t cos4t,
{g(t)}2 = 9sin4t cos2t より
(f'(t))2+(g(t))2
= 9sin2t cos2t(sin2t+cos2t)
= 9sin2t cos2t となります。
ルートをつけるということは、1/2 乗するということです。
そのため、指数法則が使えます。
つまり、
{(f'(t))2+(g(t))2}1/2
= (9sin2t cos2t)1/2
= 3| sin t cos t | となります。
三角関数の微分が出てくると、数IIで学習した三角関数の公式を合わせて考えることが多いです。
倍角の公式より、
2sin t cos t = sin2t だから、
sin t cos t = 1/2・sin2t です。
そのため、
{(f'(t))2+(g(t))2}1/2
= 3/2・| sin2t | となります。
よって、求める曲線の長さは、
3/2・∫0 |sin2t| dt となります。
変数の範囲に注目
0 ≦ t ≦ π だったので、
0 ≦ 2t ≦ 2π となっています。
絶対値が絡んでいますが、ここで数II以来の偶関数-奇関数の面積の求め方の考え方を使います。
∫0 | sin2t | dt は、
∫0 | sin2t | dt+∫π/2 | sin2t |dt です。
サインのグラフの概形から、横軸との間で囲まれている部分の面積が同じです。
そのため、絶対値がそのまま外れる方の面積だけを定積分で計算して 2 倍すれば良いということになります。
ゆえに、
∫0 | sin2t | dt
= 2・∫0 | sin2t | dt
= 2・∫0 sin2t dt です。
よって、
3/2・∫0 | sin2t | dt
= 3・∫0 sin2t dt が求める曲線の長さになります。
角度の定数倍は楽
三角関数の積分で、角度が定数倍されているときは、楽に計算できます。
置換積分を使っても計算できますが、知っていると計算が楽です。
α を定数とするとき、
∫x sin αt dt
= -1/α × [cos αt]x
今、α = 2 です。
そのため、求める曲線の長さは、次のように計算できます。
つまり、
3・ ∫0 sin2t dt
= -3/2・[cos2t]0
= -3/2・(-1-1)
= 3
この 3 が求める曲線の長さです。
数学IIIになると、公式に具体的な数を当てはめるだけでも、計算が大変になります。
既に学習した公式たちを着実に使いこなし、正確に計算をすることが大切になります。
ここから、媒介変数を意識することで、曲線の長さの公式を書き換えることを考えます。
曲線の長さ :公式の書き換え
a ≦ t ≦ b のとき、
∫a {(dx/dt)2+(dy/dt)2}1/2dx が曲線の長さの定義でした。
ここで、y = f(x) と1変数の実数値関数の形で関数の式が与えられているときの曲線の長さを考えます。
上で述べた媒介変数 t を消去した形が、このタイプになります。
そこで、
x = t, y = f(t) と媒介変数を自分で設定します。
すると、
dx/dt = 1 なので、
dy/dt = dy/dx・dx/dt
= dy/dx = f'(x) となります。
よって、
∫a {(dx/dt)2+(dy/dt)2}1/2dx
= ∫a {1+(dy/dx)2}1/2dx
= ∫a {1+(f'(x))2}1/2dx となります。
これで、y = f(x) という形の曲線についても長さを計算することができます。
具体例で練習
【練習問題】
y = x3/3+1/4x (1 ≦ x ≦ 2) で表される曲線の長さ k を求めてください。
1 ≦ x ≦ 2 なので、上端が 2 で下端が 1 の定積分を計算することになります。
f(x) = x3/3+1/4x とし、
1+(f'(x))2 を計算します。
書き換えた曲線の長さの式のルートの部分をうまく処理したいところです。
1+(f'(x))2
= 1+(x2-1/4x2)2
= (x2)2+1/2+(1/4x2)2
= (x2+1/4x2)2 です。
今、1 ≦ x ≦ 2 より、
x2+1/4x2 > 0 なので、曲線の長さの式のルートをそのまま外すことができます。
つまり、
k = ∫1 {1+(f'(x))2}1/2dx
= ∫1 {(x2+1/4x2)2}1/2dx
= ∫1 (x2+1/4x2) dx
= [x3/3-1/4x]1
= (8/3-1/8)-(1/3-1/4)
= 7/3-1/8+2/8
= 7/3+1/8
= 56/24+3/24
= 59/24
これで、59/24 が求める曲線の長さ k の値だと分かりました。
関連する記事として、
等速円運動という記事も投稿しています。
また、今回は曲線の長さを扱いましたが、曲面の面積についての数学IIIの記事も投稿しています。
球の表面積という記事で、球の表面積が導出されるにあたり、どのようなイメージなのかを解説しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。

