極大イデアル 【存在証明と必ず素イデアルとなっていることの証明】
零環ではない可換環において、" 極大イデアル “が存在することをツォルンの補題を用いて証明します。そして、その極大イデアルが素イデアルとなっていることも証明します。
可換環論の入門で、基本となる内容である「極大イデアルならば素イデアル」ということの証明は、実際に自力で証明をいつでもできるくらいまで理解をしておくと良いかと思います。
また、素イデアルで剰余環をつくると整域で、極大イデアルで剰余環をつくると、体となることは、可換環論を学習するときの基本となります。
私の経験ですが、いつでも証明ができるくらいになってくると、環論の学習がスムーズに進められるようになりました。
極大イデアルや素イデアルの定義に慣れるためにも、学習し始めの基本となる命題の証明の理解をしっかりと固めておくのが、遠回りのようでいて、近道のように思います。
では、まず極大イデアルの定義を述べ、極大イデアルが存在するということを証明します。
この記事では、環 R は可換環で、乗法単位元 1 を持っているという前提のもとで議論をしています。
極大イデアル :定義と存在証明
【定義１】
可換環 R (≠ {0}) のイデアルで、R と異なるもの全体を X とする。
そして、包含関係を X における半順序とする。
このとき、X における極大元のことを極大イデアルという。
この X は、全体 R と異なるイデアル全体なので、元が集合となっている集合系です。
半順序といっているのは、A, B ∈ X という二つの元（イデアルという集合）について、A ⊂ B でも B ⊂ A ということが起こり得るからです。
例えば、整数環 Z において、2Z というイデアルと 3Z というイデアルには、どちらも 1 を含んでいないので、全体 Z とは異なるイデアルです。
しかし、包含関係という順序について、比較不能です。
2 ∈ 2Z ですが、2 は 3Z に含まれていません。
3 ∈ 3Z ですが、3 は 2Z に含まれていません。
そのため、2Z ⊂ 3Z ではありませんし、3Z ⊂ 2Z でもありません。
このように、包含関係について、比較不能という場合があるので、最大イデアルという定義にはなっていません。
ただ、集合論入門で学習するツォルンの補題を用いることで、極大イデアルの存在が証明できます。
集合論の補題を使用
【Zornの補題】
ブログ選択公理より
≦ を順序とする半順序集合 S において、S の任意の空ではない全順序部分集合が上に有界であれば、S において極大元が存在する。
この Zornの補題では、半順序集合となっていますが、半順序集合系についても成立します。
厳密な議論は、テューキーの有限条件を集合論で学習するときに学習します。
しかし、集合論のレベルの証明を全て述べると長いので、代数学の入門では、この内容を認めて議論を進めることが多いかと思います。
この記事でも、半順序集合系 X を、R と異なるイデアルという R の部分集合全体とし、半順序を包含関係として、Zornの補題を適用します。
極大イデアルの存在証明
【定理１】
可換環 R (≠ (0)) について、R と異なるイデアル全体を X とする。
このとき、包含関係を X における半順序とすると、X には極大元が存在する。
（この極大元が極大イデアルです。）
＜証明＞
(0) = {0r | r ∈ R} = {0} は、R のイデアルなので、(0) ∈ X
このため、少なくとも 1 つは 全体 R と異なるイデアルが存在するため、X は空ではありません。
X の任意の空でない全順序部分集合系をT = {Mλ | λ ∈ Λ} とします。
次に、T が包含関係 ⊂ という順序において、上に有界であることを示します。
∪λMλ という T に含まれているイデアル全ての和集合を考えます。
この和集合が R のイデアルであることを示せば、どの T に含まれているイデアルも ∪λMλ に含まれているので、T が上に有界ということになります。
そのため、∪λMλ がイデアルであることを示せば、Zornの補題が適用でき、極大イデアルの存在が示せたことになります。
ちなみに、∪λMλ ですが、R と一致することはありません。これは、背理法という論理ですぐに確認できます。
もし、∪λMλ = R とすると、
1 ∈ R なので、1 ∈ ∪λMλ となります。
和集合の定義から、ある μ ∈ Λ が存在して、
1 ∈ Mμ となっています。
Mμ は R のイデアルなので、任意の r ∈ R に対して、r = r1 ∈ Mμ
したがって、
R ⊂ Mμ 、つまり、R = Mμ となり、
Mμ ∈ T ⊂ X が R と異なるイデアルであったことに矛盾します。
よって、背理法から ∪λMλ は R に一致していません。
このため、∪λMλ がイデアルであることを示せば、∪λMλ ∈ X となり、∪λMλ が T の上界となります。
イデアルである確認
任意の a, b に対し、和集合の定義から、ある添え字 k, h ∈ Λ が存在し、a ∈ Mk, b ∈ Mh
今、T は全順序部分集合系だったので、
Mk ⊂ Mh または Mh ⊂ Mk となっています。
Mk ⊂ Mh の場合、a, b ∈ Mh であり、Mh がイデアルであることから、
a + b ∈ Mh ⊂ ∪λMλ であり、
ra, rb ∈ Mh ⊂ ∪λMλ (∀ r ∈ R)
Mh ⊂ Mk の場合も同様に、
a + b ∈ Mk ⊂ ∪λMλ であり、
ra, rb ∈ Mk ⊂ ∪λMλ (∀ r ∈ R)
これで、∪λMλ がイデアルであることも示せたので、∪λMλ ∈ X が T の上界ということになります。
よって、Zornの補題から、R には極大イデアルが存在するということが示せました。【証明完了】
次に素イデアルの定義から説明します。
極大イデアル :素イデアルについて
【定義２】
可換環 R のイデアルで、R と異なるイデアルを P とする。
x, y ∈ R に対して、「xy ∈ P ならば、
x ∈ P または y ∈ P」となっているとき、P を R の素イデアルという。
R における乗法を計算して、積 xy が P の元になっているとすると、x か y のどちらかは P の元となっているということです。
素イデアルの身近な例です。整数環 Z について、素数 5 の倍数全体 5Z は Z のイデアルで、素イデアルとなっています。
二つの整数 x, y について、積 xy が 5 の倍数だったとします。
つまり、xy ∈ 5Z
xy の素因数分解を考えると、xy が 5 で割り切れるので、5 は x の素因数であるか、または y の素因数となっています。
5 を素因数としてもつということは、5 の倍数なので、x ∈ 5Z または y ∈ 5Z となっています。
この素イデアルの定義ですが、上で述べたことの対偶を定義とする場合もあります。
「x, y ∈ R の両方がイデアル P の元でない」ならば、「xy は P の元でない」ということです。
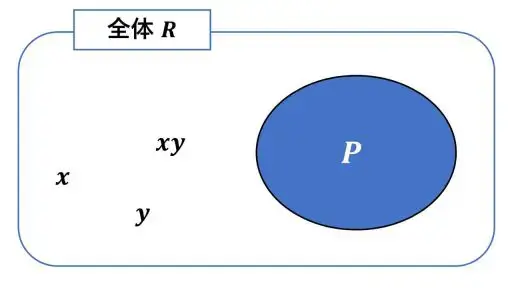
P に含まれていない R の元 x と元 y で積をとると、xy も P に含まれていないということです。
対偶に当たるのが、xy が P の元だと、x か y のうち少なくとも一方は P の元ということです。
素イデアルについての議論をするときに、どちらも使うので、可換環論の学習をするときに、慣れておくと良いかと思います。
極大イデアル → 素イデアル
【定理２】
可換環 R (≠ {0}) において、
極大イデアルならば、素イデアルである。
＜証明＞
M を R の極大イデアルとします。
この M が素イデアルの定義を満たすことを確認します。
xy ∈ M (x, y ∈ R) だとして、x ∈ M または y ∈ M となっていることを示します。
x は M の元か、 x が M の元でないかのいずれかになります。
x ∈ M だと、示したいことが成立しているので、x が M の元でない場合について議論します。
M + Rx = {a + rx | a ∈ M, r ∈ R} は R のイデアルです。
x = 0 + 1x ∈ M + Rx であり、x は M の元でない場合を考えているので、M + Rx と M は異なります。
また、M = M + 0x ⊂ M + Rx です。
今、M が極大イデアルなので、
M + Rx = R です。
※ M + Rx が R よりも小さいとすると、M よりも大きい R と異なるイデアルが存在することになり、M の極大性に反してしまいます。
よって、1 ∈ R = M + Rx
つまり、ある a ∈ R と r ∈ R が存在して、
1 = a + rx です。
この両辺に y を乗じると、y = ay + rxy
ここで、a, xy ∈ M であり、M はイデアルなので、ay, rxy ∈ M
よって、和で閉じているため、
y = ay + rxy ∈ M
したがって、y ∈ M が示せたので、素イデアルの定義が確認できました。【証明完了】
これで、可換環 R において、極大イデアルは素イデアルであることが分かりました。しかし、一般に逆は成立しません。
反例の存在
【反例】
整数環 Z 上の多項式環 Z[x] は可換環です。
(X) = {f(x)x | f(x) ∈ Z[x]} は Z[x] の素イデアルとなっています。
しかし、(x) は極大イデアルではありません。
実際、f(x), g(x) ∈ Z[x] について、
積 f(x)g(x) ∈ (x) とすると、f(x)g(x) は x で割り切れるので、f(x)g(x) の定数項は 0 でなければなりません。
Z は整域なので、零でない元どおしの積は零でないので、f(x) と g(x) の定数項は、どちらも 0 ということになります。
そのため、f(x) も g(x) も x で割り切れるため、f(x), g(x) ∈ (x) となり、素イデアルの定義を満たしていることが分かります。
(x, 2) = {k(x)x + 2h(x) | k(x), h(x) ∈ Z[x]} という二元生成のイデアルは、(x) を真に含んでいます。
(x) のどの元も x で割り切れるので、次数は 1 次以上になっています。
そのため、2 は (x) に含まれていません。
よって、(x) ⊂ (x, 2), (x) ≠ (x, 2)
となっています。
さらに、(x, 2) には 1 が含まれていないので、
(x, 2) ≠ Z[x] です。
そのため、素イデアル (x) は、包含関係における極大元ではないので、極大イデアルではありません。
ここまでの内容を踏まえて、さらに素イデアルと極大イデアルについての基本的な性質を説明します。
極大イデアル :剰余環について考える
乗法単位元 1 をもつ可換環 R が整域であるということの定義は、零ではない元と零ではない元の積が零でないということです。
文字を使って表すと、R ∋ x ≠ 0 かつ R ∋ y ≠ 0 ならば、xy ≠ 0 ということが、整域の定義です。
対偶は、「xy = 0 ならば、x = 0 または y = 0」です。
素イデアルの定義と似ています。
一般に、R のイデアル I について、剰余環 R/I を考えると、
「a + I = 0 + I (a ∈ R) 」と、「a ∈ I」は同値です。
このことから、素イデアルで剰余環を考えると、自然と次の命題が得られます。
素イデアルの同値条件
【命題１】
可換環 R (≠ {0}) のイデアルを P とする。
このとき、P が素イデアルであることと、R/P が整域であることは同値である。
＜証明＞
x, y ∈ R について、剰余環 R/P における乗法の定義から、(x + P)(y + P) = (xy) + P です。
よって、(x + P)(y + P) = 0 + P であることと、
xy ∈ P は同値です。
したがって、P が素イデアルだとすると、
(x + P)(y + P) = 0 + P であるならば、xy ∈ P となるので、x ∈ P または y ∈ P となります。
そのため、
x + P = 0 + P または、y + P = 0 + P となり、剰余環 R/P が整域であることの定義を満たします。
逆に、R/P が整域だとします。
xy ∈ P (x, y ∈ R) ならば、
(xy) + P = 0 + P なので、
x + P = 0 + P または y + P = 0 + P となります。
これは、x ∈ P または y ∈ P ということなので、P が素イデアルです。【証明完了】
この要領で、極大イデアルと、その剰余環について考えます。
極大イデアルの同値条件
【命題２】
可換環 R (≠ {0}) のイデアルを M とする。
このとき、M が極大イデアルであることと、剰余環 R/M が体であることは同値である。
＜証明＞
M を R の極大イデアルとすると、M は R と異なるので、剰余環 R/M は零環ではありません。
[K] を R/M の零ではイデアルだとすると、
ある k + M ∈ [K] (k ∈ R) が存在して、
k + M ≠ 0 + M となります。
k は M に含まれていない R の元です。
ここで、{r ∈ R | r + M ∈ R/M} という R の部分集合を K’ と置くと、K’ は R のイデアルです。
M ⊂ K’ であり、k ∈ K’ が M に含まれていないことから、K’ は M を真に含んでいます。そのため、M の極大性から、K’ は R でなければなりません。
このことから、[K] = R/M となります。
よって、R/M には零イデアルと R/M 自身しかイデアルが存在しないことが分かりました。
ゆえに、a + M ∈ R/M を R/M の零元でないとすると、(a + M) というイデアルは全体 R/M に一致します。
そのため、ある b + M ∈ R/M が存在して、
(a + M)(b + M) = 1 + M
これは、b + M が a + M の乗法逆元であることを示しています。
これで、M が極大イデアルであるならば、R/M が体であるということが示せました。
逆に、R/M が体だとします。
R/M の零イデアルでないイデアルは、乗法逆元の存在から、1 + M を含むことになります。
そのため、R/M のイデアルは零イデアルか R/M しか存在しないということになります。
これより、H を M を真に含む R のイデアルとすると、{h + M | h ∈ H} は、R/M のイデアルとなります。
M ⊂ H が真部分集合であることから、
{h + M | h ∈ H} ≠ {0 + M} なので、
{h + M | h ∈ H} = R/M となります。
よって、ある h0 ∈ H が存在して、
h0 + M = 1 + M ∋ 1 + 0 = 1
今、H ⊃ h0 + M ∋ 1 なので、H = R
したがって、M を真に含むイデアルは R しかないことが示せたので、M は R における極大イデアルです。【証明完了】
最後に、このブログサイトに投稿した環論の記事たちの内容を使って、環論を適用する練習をしてみます。
関連する内容
以前に投稿したブログ記事です。
ユークリッド整域は単項イデアル整域であり、整数環はユークリッド整域なので、単項イデアル整域となっています。
このことから、素数 p に対して、p の倍数全体から成る pZ が極大イデアルであることが次のようにして導けます。
pZ を真に含む Z のイデアル K が存在したとします。
Z が単項イデアル整域であることから、ある整数 d が存在して、K = dZ
p ∈ pZ ⊂ K = dZ より、ある整数 z が存在して、p = dz … (1)
もし、d が p の倍数だとすると、
K = dZ の任意の元が p の倍数となり、K = pZ ということになってしまいます。
これは、K が pZ を真に含むことに反してしまいますので、d は p を素因子として含んでいません。
そうすると、dz が p の倍数であることから、z が p を素因子としてもっていることになります。
よって、ある整数 t が存在して、
z = pt … (2)
(2) を (1) に代入すると、p = dpt
つまり、p(1 － dt) = 0
Z は整域であり、素数は 0 でないため、
1 = dt です。
したがって、イデアル K の生成元 d は 1 の約数なので、1 ∈ K となり、K = Z になります。
そのため、pZ を真に含むイデアルは、全体 Z しか存在しないので、pZ は Z の極大イデアルということになります。
このように、環論の基礎的な理論と少しの群の内容を知っていると、次の定理は自然と従います。
【フェルマーの小定理】
p を素数とし、n を p の倍数ではない整数とする。このとき、
ブログ「フェルマーの小定理」より
np-1 + pZ = 1 + pZ
つまり、np-1 を p で割ったときの余りは 1 ということです。
これは、pZ が Z における極大イデアルなので、【命題２】から、剰余環 Z/pZ が体となっていることから従います。
Z/pZ が体なので、零ではないイデアルは、必ず全体 Z/pZ に一致してしまいます。上の【命題２】の証明の部分で述べた内容です。
n を素数 p で割り切れない整数とすると、
n + pZ ≠ 0 + pZ となっています。
そのため、(n + pZ) という一元生成のイデアルは、全体 Z/pZ に一致します。
よって、ある x + pZ が存在して、
(n + pZ)(x + pZ) = 1 + pZ
したがって、
Z/pZ － {0 + pZ} は、位数 p － 1 の乗法群となります。
このため、n + pZ の元の位数は p － 1 の約数となるため、
1 + pZ = (n + pZ)p-1= np-1 + pZ
このように、大学受験などの発展内容として出てくるフェルマーの小定理が、環論の入門内容とつながっています。
読んで頂き、ありがとうございました。
これで、今回のタロウ岩井の記事を終了します。