二重根号の外し方 | ルートをつけるということは1/2乗するということ

" 二重根号の外し方 “について、高校に入学した頃に、公式に数を当てはめることから学習を始めます。
学習進度が進むと、数学IIの内容を見据えて、二重根号の外し方を捉え直します。
数学Iで学習するルートをつけるということは、1/2乗という有理数乗という見方ができます。
そうすることで、数学IIの指数を見据えることができます。
高校に入学したばかりの段階だと計算が厳しいかと思いますが、このブログ記事は、高校二年の数学へのつながりを意識して有理数乗についての指数計算へと踏み込んでいます。
まずは、具体的な数を使って、二重根号を外してみます。その後で、文字を使って一般化するようにします。
※ 目次の項目を選択すると該当箇所へ移動します。
二重根号の外し方 :ルートは1/2乗
このブログ記事の表紙の画像では、ルートの中にルートがあります。二重にルートがあることから、二重根号というわけです。
このブログ記事では、ルートをつけるというを1/2乗をするという見方をします。そうすると、指数法則が使えます。
本格的に、数学IIで、指数が有理数のタイプを学習するのですが、いきなり有理数を学習すると混乱するかと思います。
そこで、高校一年の計算公式が使えるようになってきたら、1/2乗を機会に、有理数についての指数法則を使うと良いかと思います。
私自身の高校一年の頃の経験談です。
「どっちみち今後は有理数乗についての計算をすることになるので、それなら高校一年の段階から、できる部分は普段の計算で練習しておく」ということを実践していました。
高校で学習することが多いので、数学IIの内容でも、早くから習得できるのなら、早くから使って慣れておくと、数学IIの今後の学習の負担を減らすことができます。
このような当時の自分の経験から、二重根号の外し方について、今回のブログ記事を投稿しました。
ルートをつけるということは1/2乗をするという観点で、二重根号を扱います。
二重根号の具体例
【例題1】 (10 + 2 × 211/2)1/2
これが表紙の画像に記していた二重根号の式です。1/2乗を用いて表すと、このようになります。
分数乗になっていますが、
(xa)b = xab という指数法則が使えます。
a や b の指数の部分に 1/2 のタイプが二重根号です。
【例題1】では、x の部分に該当する形になっていないので、10 + 2 × 211/2 を xa の形に変形したいところです。
法則が使える形へ変形
方針が固まったので、式を書き換えます。
和 10 で、積 21 ということで、
7 + 3 と 7 × 3 と当たりをつけます。
(st)a = sata の指数法則を使うチャンスです。
211/2 = (7 × 3)1/2
= 71/2 × 31/2 となります。
さらに指数法則で、
(71/2)2 = 71/2×2 = 71,
(31/2)2 = 31/2×2 = 31
71 や 31 は、7 と 3 なので、
10 = 7 + 3
= (71/2)2 + (31/2)2
では、赤色で書き換えた内容を一つにまとめます。
10 + 2 × 211/2 =
(71/2)2 + (31/2)2+2×71/2 × 31/2
加法の順番を入れ替えると、
10 + 2 × 211/2 =
(71/2)2+2×71/2 × 31/2+(31/2)2
= (71/2 + 31/2)2
二乗の因数分解公式が使える形になっていました。
これで、目指していた括弧の中を xa という形にすることが達成できました。
(10 + 2 × 211/2)1/2
= {(71/2 + 31/2)2}1/2
= (71/2 + 31/2)2×1/2
= (71/2 + 31/2)1= 71/2 + 31/2 となり、二重根号が外れました。
高校一年の計算だと、1/2乗をルートをつけた形にして答案とします。
ただ、数学II や、理系だと数学IIIで、このようなルートの計算を頻繁に行います。
1/2乗についての計算に、少しづつ慣れていくことで、高校二年や高校三年になったときに、これくらいの計算を使いこなせるようになってくるかと思います。
ただ、高校に入学した段階だと、この指数計算は厳しいものがあると思います。
焦らず徐々に計算レベルを引き上げるものと思っておくと良いかと思います。
上で述べた内容を、文字を使って一般化します。
二重根号の外し方 :文字を使って一般化

a ≧ 0, b ≧ 0 という条件は、二重根号を外したときに、ルートの中が負の実数だと、虚数になることを除いています。
※ 虚数(複素数)は数学IIで学習します。
a - b ≧ 0 の条件よって、【公式2】の方で、二重根号を外したときに、絶対値をそのまま外せるようになります。
絶対値について、実数 a に関して、
(a2)1/2 = | a |
例えば、a = -5 のとき、
(a2)1/2 = {(-5)2}1/2 = 251/2
= 5 = -(-5) = -a
負の実数が絡むときには符号に注意です。
それでは、【公式1】から証明します。
【公式1】の証明
指数法則より、
{a+b+2(ab)1/2}1/2 =
{(a1/2)2+(b1/2)2+2(ab)1/2}1/2 =
{(a1/2 + b1/2)2}1/2 = |a1/2 + b1/2|
a ≧ 0, b ≧ 0 なので、
a1/2 + b1/2 ≧ 0 だから、
絶対値はそのまま外れるので、
{a+b+2(ab)1/2}1/2
= a1/2 + b1/2【証明完了】
続いて、【公式2】の証明です。
同じく二乗の因数分解を使うのですが、
a ≧ 0, b ≧ 0 だけの条件だと、
a - b の符号が分かりません。
a - b ≧ 0 という条件が効いてきます。
【公式2】の証明
指数法則より、
{a+b-2(ab)1/2}1/2
= {(a1/2)2+(b1/2)2-2(ab)1/2}1/2
= {(a1/2- b1/2)2}1/2
= |a1/2- b1/2|
ここで、a - b ≧ 0 より、
a ≧ b ≧ 0 なので、a1/2 ≧ b1/2
※ 二次関数 y = x2 のグラフをイメージすると、y 軸で a ≧ b ≧ 0 のときに、x 軸上の対応する点を見ると、a1/2 ≧ b1/2 となっています。
よって、a1/2 - b1/2 ≧ 0 なので、
|a1/2 - b1/2| = a1/2 - b1/2 だから、
{a+b-2(ab)1/2}1/2
= a1/2 - b1/2【証明完了】
では、証明した公式を使う例題を解いてみます。
2(ab)1/2 の 2 が、与えられた式に現れていないときは、公式が使える形に変形します。
二重根号の外し方 :公式が使える形へ変形
【例題2】 (3 - 51/2)1/2
これは、いきなり出てくると、気づきにくいかと思います。
ルートに関して使える式の書き換えです。
5 = 4 × 1/4 × 5 だから、
51/2 = 1/2 × 2 × 51/2 … (1)
さらに、約分すると、
3 = 1/2 × 6 … (2)
(2) - (1) より、
3 - 51/2 =
1/2 × 6 - 1/2 × 2 × 51/2
右辺で 1/2 は共通因数だから、
3 - 51/2 =
1/2 × (6 - 2 × 51/2)
和 6, 積 5 の形で、2 が 51/2 に掛けられています。
では、これらをまとめて、答えを求めます。
【例題2】の答え
(3 - 51/2)1/2
= {1/2×(6-2×51/2)}1/2
= (1/2)1/2×{(6-2×51/2)}1/2…(あ)
ここで、5 + 1 = 6, 5 × 1 = 5 なので、
【公式2】から、
{(6-2×51/2)}1/2
= 51/2 - 11/2
= 51/2 - 1 … (い)
(い) を (あ) に代入すると、
(3 - 51/2)1/2 =
(1/2)1/2×(51/2 - 1)
ここで、分母にルートがきている形なので、有理化をします。
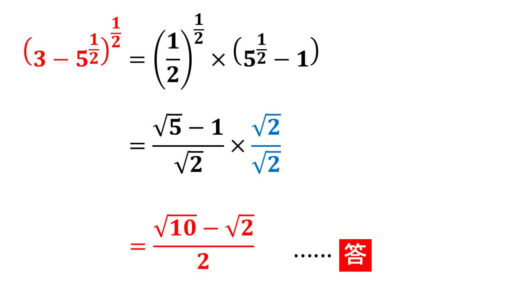
(1/2)1/2 = 1/(21/2) と分母にルートが現れていた部分を解消できました。
これで、有理化も完了して、求める答えとなりました。
有理化の部分は、数IIの指数が有理数のときの計算を意識した計算をしました。この部分は、自分にとって分かりやすいような形で計算をすれば良いかと思います。
それでは、これで今回のブログ記事を終了します。
数学I の計算内容について、複二次式など、他にも記事を投稿しています。
また、分数指数という記事では、数IIの指数計算の内容を出力するコード入力について解説をしています。
今回の記事で、和と積の値という二次方程式の解と係数の関係の考え方を述べました。
今回のブログ記事の内容は、数学IIの指数計算を意識した内容にしました。
2/3乗や-5/3乗といった計算が出てくるのが数学IIです。
数学I から数学II への架け橋となることを狙いましたが、数学II の有理数乗の指数計算は、いきなり学習をすると、大変なので、1/2乗で前もって慣れておくと良いかと思います。
読んで頂き、ありがとうございました。