分点公式 | 内分点と外分点の比とベクトルの計算

" 分点公式 “での内分や外分のベクトル表示を考えるときに、ベクトルの加法(和)が基本となります。
減法が加法から誘導された演算ということから、加法を中心に議論を進めることができます。
サムネイルに記しているのが、ベクトルの分点公式です。内分点の公式と外分点の公式です。分点比が分かると、これらの公式を使うことができます。
また、既に証明されている定理を用いて分点比を求めてから、ベクトルの分点公式を使う練習をしておくと良いかと思います。
ベクトルの加法と、加法から導かれる減法、そしてスカラー倍での伸縮が基本になります。
マイナスの実数でスカラー倍をすると、ベクトルの向きが逆転することが、減法が加法から導かれる理由です。
図形的な内容とベクトルの計算を合わせて、分点の位置をベクトルで表示することを解説します。
分点公式に慣れていると、すぐに公式に当てはめてベクトルの式を導けます。
ただ、内容を理解したり、落ち着いてミスが無いかを確認したりするために、公式を証明するように手順を具体的に解説します。
分点公式 :加法から始める
ベクトルの加法と減法の関係ですが、文字式の減法の要領で計算ができます。
x - y = x + (-y) というように、減法は符号を逆転させたものとの加法です。そのため、減法を加法に直すことで、加法を用いて減法を考えることです。
ちなみに、ベクトルを -1 でスカラー倍をすると、大きさがそのままで、向きが逆転したベクトルになります。
減法が出てきたときは、向きを逆転させたベクトルとの加法を考えるということが基本になります。
このことを押さえておくと、落ち着いてミスが無いかを確認することができるので、見直しをして着実に問題を正解することも可能になるかと思います。
それでは、具体的な例を通して、分点公式を使ってみます。
内分点の公式
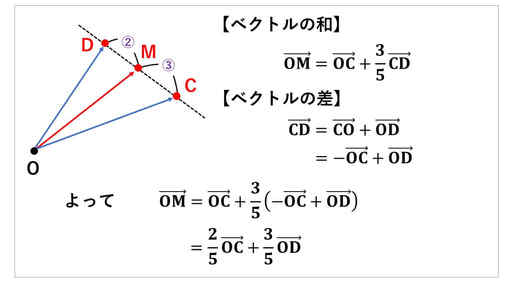
CM : MD が 3 : 2 と線分 CD の内分比が求まっていたとします。
ここから、ベクトルの内分点の公式を使うと、ベクトル OM を上の図の一番下に書いているように表すことができます。
まず、求めたいベクトル OM をベクトル OC とベクトル CD の 3/5 倍の和として表します。ベクトル CD は始点が O でないので、始点を O にそろえます。
ベクトルの差で混乱をしたら、やはり差を和で表すことができるので、焦らないことが大切かと思います。
ベクトル CD は、点 C から点 D への矢印です。「点 C から点 O を経由して点 D へ」と考えると、ベクトル CO とベクトル OD との和になります。
後は、-1 倍をしてベクトル CO をベクトル OC に書き換えます。
すると、ベクトル CD を図の真ん中に書いているように、始点を O にした式に直すことができます。
ベクトル CD を始点が O になるように書き換えた式を、ベクトル OM の式に代入をして整理します。
すると、ベクトル OM を、すべて始点が O になっているベクトルで表せます。
これで、サムネイルに記していた内分点の公式を適用した式になりました。
ここまでの内容は、公式に慣れていると一瞬です。
しかし、加法とスカラー倍の内容から検証できるようになるためにも、理解を深めるために、公式を証明する過程を述べました。
では、次に外分について扱います。
外分点の公式
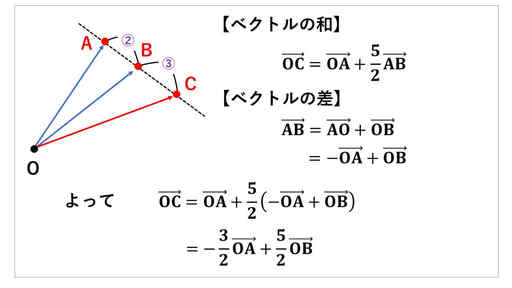
点 C が外分点のときですが、外分比が分かったら、外分点の公式で始点が点 O にそろったベクトルの和の形で表せます。
外分比の公式は、よく混乱するので、自分でベクトルの和に基づいて確かめをしておいた方が良いかと思います。
ベクトル AB をベクトルの差を使って表しています。上の図の【ベクトルの差】と書いている式をご覧頂くと、-1 倍をして、向きを逆転させたベクトルとの加法で考えています。
-1 倍して向きを逆転させたベクトルとの和で式を書き換えることは、役に立ちます。
点 O から点 C へ行くには、「点 O → 点 A → 点 C」なので、ベクトル OA とベクトル AB の 5/2 倍の和と表せます。
後は、内分比のときと同じ要領で、ベクトル AB を点 O が始点になるように書き換えます。そうすると、始点が点 O にそろったベクトルの和の式に辿り着きます。
ここまでの例では、分点比がはじめから示されていました。しかし、実際に問題を解くときに、自分で分点比を求めるところから議論をしなければならないときもあります。
今度は、既に数学Aの平面図形で学習した定理を使って分点比を求めるところから解説をします。
分点公式 :分点比をまず求めてから
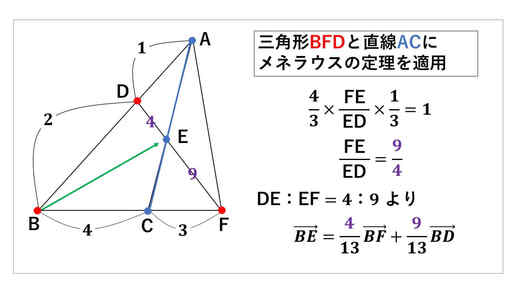
図のベクトル BE を求める練習問題と思って、ご覧ください。
実際の問題では、DE : EF = 4 : 9 ということを自分で求めてから分点公式を使うことになります。
このキツネみたいな図で、
メネラウスの定理を三角形 BFD と直線 AC に対して適用すると、DE と EF の比が分かります。
そうすると、三角形 BFD において、DF を 内分している点が E なので、内分点の公式を先ほどと同じように使えます。
図の一番下に書いている式がベクトル BE を表す式です。
このように、先に分点比を求めておいてから、分点公式を使うという流れの問題が出題されることがあります。
議論の流れを考えて、着実に進めることが大切になります。
この練習問題に関連して、数学の推論について述べておきます。
数学の推論
数学で議論を進めるときに、今の議論の真偽とは別に、既に成立している正しい命題(真である命題)を適用できるときがあります。
命題を適用できるときは、命題の結論以外のすべての内容を満たしているときになります。
先ほど数学Aの定理を適用しましたが、その定理の結論以外のすべての条件を満たしていたからです。ただ単に三角形と直線があるだけでは定理が適用できるかどうかは定かではないので注意です。
定理の適用にあたって、既に成立している命題が適用できるかどうかを判断するためには、命題がどのような構成になっているのかを押さえておく必要があります。
命題-仮定-結論というブログ記事で、この命題の構成について詳しく解説をしています。
結論以外のすべてに当てはまっているときに、その命題の結論へと議論をジャンプさせることができます。
この推論規則を正しく使えるようになっておくと、数学の学習が楽になります。
高校の数学のベクトルで、図形についての内容を足掛かりにしながら、数学の論理とベクトルの計算を合わせて学習をしておくと、大学の数学への良い準備になるかと思います。
大学の数学のベクトルだと、抽象的な文章が多いので、図からの内容を参考にでき、正しい推論の規則の良いインプットとアウトプットができると思います。
今回のブログ記事では、ベクトルの分点公式の使い方について解説をしました。線分比からベクトルを用いて内容を表現するという内容でした。
右上の ≡ のところにサイトマップというこの数学サイトの記事をまとめたページを用意しています。
そこから、既に投稿したブログへジャンプできるのですが、まさに、この内容が既に成立している命題を適用するという内容の応用になります。
最後に、内分と外分と合わせて、斜めに交わる(平行でない)二つのベクトルで張られる平面について説明します。
斜交なベクトル
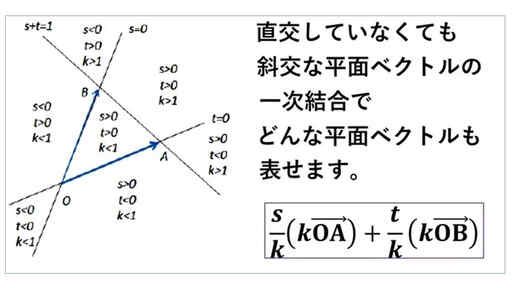
図で、平行ではない二つの零ではないベクトル OA と OB によって、一つの平面が張られています。
張られるというのは、二つのベクトルの一次結合で平面上のどの点も表されているということです。
図の右下の括弧で囲っている式で、s, t, k の値によって、どの部分に一次結合の計算結果となるベクトルがあるのかということも概算で分かります。
「s + t = 1」のときと、「s + t = k ≠ 0」で場合分けをして考えた図です。
s + t = 1 のときは、一次結合によって表される点が、線分 AB を内分もしくは外分していることです。この 1 は百パーセントの 1 です。
抽象的な図なので、具体的に s, t, k に数字を当てはめたものを見てみます。
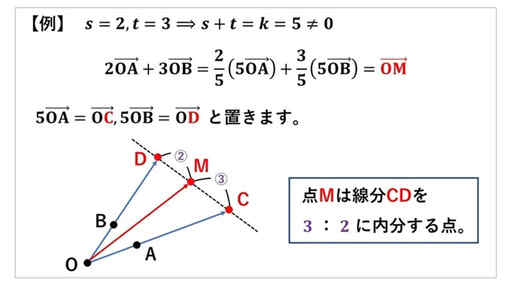
分数の計算が厄介ですが、s = 2, t = 3 のとき、s + t = k = 5 ≠ 0 のときに、一次結合の結果の終点 M がどこにあるのかを把握することができます。
点 C と点 D を置いたのは、図形的な位置を示す記号が欲しかったからです。
ちょうど、スカラー倍を表している分数の和が 1 になるようにベクトルの式を書き換えました。直線 CD を出現させて、内分点の公式にあてはめて、点 M の位置を記述しました。
もう少し、平行ではない二つのベクトルについて説明します。平行ではないということを示すのに、背理法は効果的です。
背理法で平行でないことの証明
(1, 2) という平面ベクトルと、(5, 3) という平面ベクトルを考えます。どちらも零ベクトルではありません。
また、内積を計算すると、
1 × 5 + 2 × 3 ≠ 0 なので、垂直ではありません。
片方のベクトルを適切に実数倍したとき、もう片方のベクトルになるときに、二つのベクトルは平行であるということになります。
今回の (1, 2) と (5, 3) は平行ではありません。
よって、斜交である平面ベクトル {(1, 2), (5, 3)} が基底となります。
一次独立であり、一次結合で表されるベクトル全体が平面ベクトル全体と一致するということです。
どちらも零ベクトルでなく、平行でもない二つのベクトルの一次結合全体で、すべての平面ベクトルが表されます。
(1, 2) と (5, 3) が平行では ないことを以下で、背理法を用いて証明します。
もし、p(1, 2) = (5, 3) となる実数 p が存在したと仮定をして、矛盾を導きます。
そうすると、背理法より、そのような実数が存在しないということになり、平行ではないということが分かります。
P(1, 2) = (p, 2p) ということから、x 成分について、p = 5 です。
一方、y 成分について 2p = 3 となり、p = 3/2 となります。
そのため、実数 p は 5 という整数であり、なおかつ 3/ 2 という分数ということになり矛盾します。
したがって、(1, 2) をどんな実数倍をしても、(5, 3) にはならないということになります。これで、平行ではないということが証明できました。
今、背理法を使って証明をしましたが、別の示し方もあります。
具体的な数字で成分が書かれているときには、直線の傾きを考えるのも一つの手です。
(1, 2) という平面ベクトルは、原点を始点とし、終点が点 (1, 2) です。
したがって、2 点 (0, 0) と (1, 2) を通る直線の上に乗っています。
原点から x 軸方向に 1 進み、y 軸方向に 2 だけ進むと変化の割合である直線の傾きです。
したがって、傾きは 2 ÷ 1 より、2 です。
同じく (5, 3) の傾きは、3 ÷ 5 = 0.6 です。
傾きが異なる二直線は平行ではないわけです。
関連する平面ベクトルの内容で、
内積の定義という記事を投稿しています。
それでは、これで今回のブログ記事を終了します。
読んで頂き、ありがとうございました。