第二同型定理 | 群論入門で学習する基本となる定理の一つ【第三同型定理も】

" 第二同型定理 “を群論入門で学習します。群についての準同型定理から導かれる定理で、入門内容を理解していくときに、山場へとさしかかってくる内容になります。
第一同型定理から導かれる定理ですが、一つ補題を用意し、その補題と第一型定理から導きます。
既に証明されている第一準同型定理を使うときに、その定理のどの部分群に、どんな部分群が該当しているのかを正確に押さえることが大切になります。
また、記事の最後では、第三同型定理も導いています。
第一同型定理を基礎として導くので、土台となる準同型写像について復習を兼ねて述べておきます。
第二同型定理 :準同型の復習
【準同型写像の定義】
G, G’ を群とし、G から G’ への写像 f が次を満たすとき、f を群準同型写像という。
すなわち、
f(gh) = f(g)f(h) (∀g, h ∈ G)
始集合である G の任意の元 g, h に対して、積をとってから f で移すのと、f で移してから終集合である G’ において f(g) と f(h) で積をとるのが等しいということです。
この準同型写像の定義から、
ker f = {g ∈ G | f(g) = e’} が G の正規部分群ということが導かれます。
e’ を G’ の単位元としたとき、G の元で f によって e’ へと移される元を全て集めたものです。
この ker f が G の正規部分群となっているので、剰余群 G/ker f が定義できます。
G/ker f と Im f が群として同型になるというのが群としての準同型定理です。
Im f = G’ となっているとき、すなわち、f が全射であるときは、G/ker f と G’ が群として同型ということになります。
ここまでの内容を定理として、まとめておきます。
使う定理
【第一同型定理】
f : G → G’ を群準同型写像とする。
このとき、G/ker f と Im f は群として同型である。
Ψ : G/ker f → Im f を Ψ(gker f) = f(g) と定義すると、群としての同型写像になっています。
この第一同型定理という群についての準同型定理を証明します。
<証明>
まず、Im f = { f(g) | g ∈ G} が G’ の部分群となっていることから確認します。
x, y ∈ Im f とするときに、xy-1∈ Im f であることが次のようにして分かります。
Im f の定義から、ある g, h ∈ G が存在して、
f(g) = x, f(h) = y と表すことができるので、
xy-1 = f(g)(f(h))-1
=f(g)f(h-1) = f(gh-1)
gh-1 ∈ G なので、
xy-1 = f(gh-1) ∈ Im f です。
よって、Im f は G’ の部分群となっています。
N = { g ∈ G | f(g) = e’ } = f-1(e’) が G の部分群になっていることも、同じ要領で確認することができます。
g, h ∈ N = { g ∈ G | f(g) = e’ } に対して、
f(gh-1) = f(g)f(h-1)
= f(g)(f(h))-1 = e'(e’)-1 = e’
よって、gh-1 の f による像が e’ なので、
gh-1 ∈ N です。
さらに、N が G の正規部分群であることを確認します。
任意の x ∈ G, h ∈ N に対して、
f(xhx-1) = f(x)f(h)f(x-1)
= f(x)f(h)(f(x))-1
= f(x)e'(f(x))-1
= f(x)(f(x))-1 = e’
よって、xhx-1 ∈ N より、xNx-1 ⊂ N です。
そのため、
任意の x ∈ G に対して、xNx-1 = N となるので、N は G の正規部分群です。
このことから、剰余群 G/N が定義できます。
gN ∈ G/N に対して、f(g) ∈ Im f を対応させる 写像を Ψ とすると、Ψ は G/N から Im f への群同型写像となります。
Ψ が矛盾なく定義できているところから確認します。
xN = yN とすると、ある z ∈ N が存在して、
x = yz と表せます。
Ψ(xN) = f(x) = f(x)e’ であり、
e’ = f(z) なので、
Ψ(xN) = f(x)
= f(yz) = f(y)f(z)
= f(y)e’ = f(y) = Ψ(yN)
xN = yN のとき、Ψ(xN) = Ψ(yN) となっていて、Ψ が矛盾なく定義できていることが分かりました。確かに一対一対応となっています。
Ψ が群準同型写像となっていることは、f が群準同型写像であることから従います。
任意の aN, bN ∈ G/N に対して、
a, b ∈ G だから f(ab) = f(a)f(b) となるので、
Ψ((aN)(bN)) = Ψ((ab)N) =
f(ab) = f(a)f(b) = Ψ(aN)Ψ(bN)
これで、Ψ が G/N から Im f への群準同型写像となっていることが分かりました。
任意の c ∈ Im f に対して、Im f の定義から、g ∈ G が存在して、f(g) = c と表せます。
この g について、gN を Ψ で移すと、
Ψ(gN) = f(g) = c
よって、Ψ は全射です。
Ψ が単射であることは、次のようにして示せます。
Ψ(xN) = Ψ(yN) (x, y ∈ G) とすると、
Ψ(xN)(Ψ(yN)-1 = e’ なので、
f(xy-1) = Ψ((xy-1)N) = e’
xy-1 ∈ N となっているので、ある z ∈ N が存在して xy-1 = z となるので、x = zy です。
Nz = N なので、N が正規部分群であることから、
xN = Nx = N(zy) = Ny
これで、Ψ が単射であることも示せました。
以上より、Ψ は群準同型写像で全単射となっています。【証明完了】
この準同型定理と合わせて、メインの第二同型定理を証明するときに使う補題を証明します。
この補題なくしては、第二同型定理という命題自体が存在し得ないものになってしまうので、基礎として押さえておく必要がある補題になります。
第二同型定理 :補題の証明
【補題】
群 G の部分群を H, 正規部分群を N とすると、
HN = {xy | x ∈ H, y ∈ N} は G の部分群である。
<証明>
a, x ∈ H, b, y ∈ N とすると、
(ab)(xy)-1 = (ab)(x-1y-1)
= a{(bx-1)y-1} … (1)
N は正規部分群なので、Nx-1= x-1N なので、ある z ∈ N が存在して、bx-1 = x-1z と表すことができます。
これを (1) に代入すると、
(ab)(xy)-1 = a{(x-1z)y-1}
= (ax-1)(zy-1)
ax-1 ∈ H, zy-1 ∈ N より、
(ab)(xy)-1 ∈ HN【証明完了】
任意の二つの元について、片方を逆元として積をとると、積で閉じていることを示すと、部分群ということになります。
※ 部分群の判定方法という記事で、この部分群であることの証明方法について解説しています。
N が G の正規部分群となっているということから、一般の結合律を使って、議論を進めました。
結合律は、半群の段階で成立しますが、環論などでも、よく使います。
※ 一般の結合律については、リンク先のブログで証明しています。
4 個以上の任意の有限個数で括弧のつけ方に依らずに積の値が、ただ一通りに定まるということを示す定理になります。
それでは、メインの定理を証明します。今、示した HN が部分群となっていることが、前提として使われています。
定理の証明
【定理】
群 G の部分群を H とし、G の正規部分群を N とする。
このとき、H ∩ N は H の正規部分群で、
HN/N と H/H ∩ Nは群として同型となる。
<証明>
任意の h ∈ H に対して、
h(H∩N)h-1 ⊂ hHh-1 = H,
h(H∩N)h-1 ⊂ hNh-1 = N
よって、h(H∩N)h-1 ⊂H∩N なので、
H∩N は H の正規部分群です。
また、先ほど示した【補題】より、HN は G の部分群で、N = eN ⊂ HN
したがって、N は HN の正規部分群にもなっています。
※ H = He ⊂ HN より、H は HN の部分群になっています。
f : H → HN/N を x ∈ H に対して、
f(x) = xN と定義します。
a, b ∈ H に対して、
f(ab) = (ab)N
= (aN)(bN) = f(a)f(b)
ゆえに、f は準同型写像となっています。
また、任意の h ∈ H, g ∈ N に対して、
(hg)N = hN より、f(h) = hN = (hg)N
よって、f は全射で、Im f = HN/N
{h ∈ H | f(h) = eN} が H ∩ N と一致していることを示します。
x ∈ H∩N とすると、x ∈ N より、
f(x) = xN = eN (= N) なので、
H ∩ N ⊂ { h ∈ H | f(h) = eN}
a ∈ { h ∈ H | f(h) = eN} とすると、
aN = f(a) = eN より、a ∈ N です。a は H の元でもあったので、a ∈ H∩N
このことから、
{ h ∈ H | f(h) = eN} ⊂ H ∩ N
よって、{ h ∈ H | f(h) = eN} が、
H ∩ N と一致していることを示せました。
ゆえに、第一同型定理から、
H/H∩N と Im f = HN/N が群として同型となっています。【証明完了】
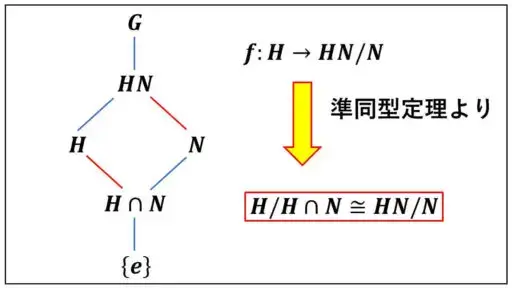
今、証明をした第二同型定理は、シローの定理の一つで「p-部分群は必ずシローp-部分群に含まれる」という内容を証明するときに役に立ちます。
最後に、第三同型定理も証明しておきます。
見かけが複雑そうですが、第一同型定理に当てはめることで得られます。
Im f と f-1(e’) が、何に当たるのかということを押さえてから、第一同型定理を適用すると証明が完了します。
第三同型定理
【定理】
群 G の正規部分群を H と N とする。
そして、H ⊂ N とする。
このとき、(G/H)/(N/H) は G/N と群として同型である。
<証明>
f : G/H → G/N を f(gH) = gN と定めます。
g1H = g2H とすると、ある h ∈ H が存在して、g1 = g2h と表せます。
そして、H が N に含まれているという仮定から、hN = N となります。
よって、
f(g1H) = g1N = (g2h)N
= g2(hN) = g2N = f(g2H)
ゆえに、f(g1H) = f(g2H) となっているので、f は矛盾なく定義できています。
任意の xN ∈ G/N に対して、
xH ∈ G/H の f による像は、
f(xH) = xN だから、f は全射です。
そのため、Im f = G/N となっています。
aH, bH ∈ G/H とすると、
f((aH)(bH)) = f((ab)H) = (ab)N
= (aN)(bN) = f(aH)f(bH)
より、f は群準同型写像です。
また、N/H ⊂ G/H であり、
任意の xH ∈ N/H に対して、x ∈ N なので、
f(xH) = xN = N = eN となり、xN の f による像は G/N の単位元 eN です。
逆に、gH ∈ G/H で f(gH) = eN とすると、
gN = eN = N なので、g ∈ N となります。
これは、gH ∈ N/H ということになります。
よって、
{gH∈G/H | f(gH)=eN} = N/H
以上より、第一同型定理より、
(G/H)/(N/H) と G/N が群として同型ということが示せました。【証明完了】
* 第一同型定理における f-1(e’) を f-1(eN) として適用しました。
群論入門については、他に共役類 類等式という記事も投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。