対角線が中点で交わる四角形 | 高校で扱う十分性の確認
" 対角線が中点で交わる四角形 “などの図形を用いて、" 十分性の確認 “について大学受験の数学を視野に入れて解説をしています。
高校で学習をする論理の内容になるので、難しい感じがします。
しかし、中学の数学の図形の単元で、この内容は既に経験をしています。
高校の内容を題材にすると複雑になるので、よく知っている中学で学習をした図形を使って高校で学習する論理や集合について解説をするようにします。
条件 p が与えられたときに、条件 p を満たすもの全体が、どういう集合になっているのかを調べるときに十分性の確認といわれている流れで考察を進めることがあります。
まず高校で学習する内容を述べた後、中学で学習した図形を用いて詳しく内容を掘り下げます。
対角線が中点で交わる四角形 :一般的な流れと記号
条件 p が与えられたという状況を考えます。
このときに、条件 p を満たす集合 A が何かということを調べたいときが出てきます。
そのときに、条件 p を満たすときに、必ずこの集合 B に含まれるということを仮で求めるという思考の流れを考えます。
ストレートに集合 A を確定できれば良いのですが、A について検討がつきにくいときに、いったん集合 B の枠内であると仮の枠を求めます。
この集合 B に含まれる条件を必要条件といいます。
つまり、
条件 p が与えられたとき、
「条件 p ならば 条件 q」という命題が真(正しい)となる条件 q を満たす集合 B を求めるということです。
※ 命題・仮定・結論という高校の数学の記事を投稿し、命題というものについて詳しく説明をしています。
「条件 p ならば 条件 q」という命題が真であるとき、ならばの前の条件である仮定条件 p のことを十分条件といい、結論条件 q を必要条件といいます。
条件 p が与えられたときに、「条件 p ならば 条件 q」という命題が真となる条件 q を求めることを必要条件を求めるといいます。
この必要条件 q を満たす集合 B について、「条件 p ならば 条件 q」という命題が真となっているとき、仮定条件をみたすもの全体から成る集合 A が集合 B に含まれているという状態になります。
一般に、集合 A が何かを決定する前段階として集合 B が何かということを考えます。
集合 B の方が、求めやすいとでも思っておいてください。
A ⊂ B となるように、条件 q を求めるということが最初の一手となります。
ここで次の二つの可能性が出てきます。
一致しているかどうか
条件 p を満たすもの全体から成る集合 A, 条件 q を満たすもの全体から成る集合 B について、「条件 p ならば 条件 q」という命題が真という状態を考えています。
このとき、
A ⊂ B と記号で表すのですが、A が B の部分集合となっています。
※ 要素(元)という記事で、高校の数学で使う部分集合について詳しく解説をしています。
ここで、集合 A と集合 B が一致していない場合と、一致している場合に分かれます。
集合 A が何かということを考えるときの次のステップが、一致していないのか一致しているのかの見極めになります。
A ⊂ B という状況で、A に含まれないが B の要素となっているものが存在するときが、一致していないということです。
一致していない場合だと、B の要素だけれども A に含まれていない要素を、すべて B から除外すると、集合 A となります。
一致していないときは、これで集合 A がどういった集合かを確定させます。
次に、集合 A と集合 B が一致している場合についてです。
このときは、A = B となっているので、
B ⊂ A となっています。
そのため、
「条件 q ならば 条件 p」という命題も真となっています。
したがって、A と B が一致していると考えたときは、「条件 q ならば 条件 p」という命題を証明します。
これらのように、必要条件を満たすものが十分条件を満たすかを確認することを、この記事のタイトルにしている十分性の確認といいます。
必要条件を満たすもののうち、十分条件を満たさないものは除外する、また、十分条件を満たさないものが1つも無いと考えるときは逆を証明するということになります。
ここまで、高校の数学で使われる論理や集合の記号を使って述べてきましたが、十分性の確認ということを具体的な例を使って実践してみます。
十分性の確認 :実践練習
ここからは、中学の数学で学習した平行四辺形を使って論理を運用することについて述べます。
平行四辺形について、次の内容が既に分かっていることとします。
平行四辺形について、次の①から③は同値である。
① 向かい合う2組の辺がそれぞれ平行である。
② 向かい合う2組の辺がそれぞれ等しい。
③ 向かい合う2組の角の大きさがそれぞれ等しい。
ブログ平行四辺形-定義より
①が四角形が平行四辺形であることの定義です。
そして、四角形について、①から③の条件は、どの2つも必要十分条件となっています。
同値なので、四角形が、どれか1つの条件を満たすと、残りの二つの条件も満たすことになります。
例えば、四角形が②を満たしていたとします。
必要十分条件なので、特に「②ならば①」は真です。
今、②を満たしているので、①を満たすということにもなります。
このようにして、①から③の条件のうち、1つでも満たすと残りの2つの条件も満たすということになります。
同値なので、状況に応じて適切な条件に書き換えて使うことができて便利です。
この平行四辺形について、議論をすることにします。
条件 p として「平行四辺形である」という条件を考えます。
四角形が、この条件 p を満たしたとき、「条件 p ならば 条件 q」が真となる条件 q を求め、十分性を確認します。
四角形ABCD が、条件 p を満たすときに次の二つのことが分かります。
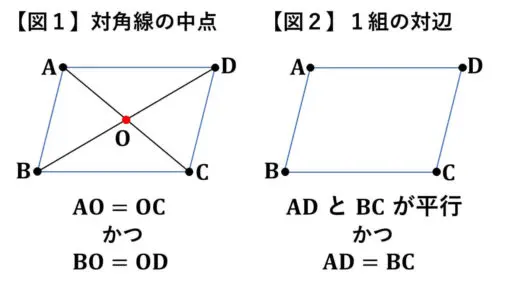
【図1】は、対角線がそれぞれの中点で交わるという内容です。
【図2】は、1組の向かい合う辺が等しく平行であるという内容です。
後で【図2】についても議論をしますが、先に【図1】について議論することにします。
「対角線がそれぞれの中点で交わる」という内容が条件 q となるだろうと考えます。
条件 p に当てはまっている内容を吟味して、必要条件となる内容を考えます。
本当に必要条件となっているのかを示すためには、「条件 p ならば 条件 q」という命題が真ということを証明します。
もしくは、条件 p を満たすもの全体から成る集合 A が、条件 q を満たすもの全体から成る集合 B に含まれているということを示すことになります。
では、実際に必要条件となっていることを示しています。
対角線がそれぞれの中点で交わる四角形
【命題1】
四角形ABCD について、
四角形ABCD が平行四辺形ならば、対角線がそれぞれの中点で交わる。
<証明>
対角線AC と BD を引き、それらの交点を O と置くことにします。
△ABO と △CDO について、合同となっていることを示します。
四角形ABCD が平行四辺形なので、
平行四辺形の定義①から、
AB // DC となっています。
平行な直線の錯覚が等しいため、
∠BAO = ∠DCO …(1)
∠ABO = ∠CDO …(2)
また、四角形ABCD が平行四辺形なので、
②から向かい合う辺がそれぞれ等しくなっています。
そのため、
AB = CD …(3)
(1), (2), (3) より、1組の辺とその両端の角がそれぞれ等しいことから、
△ABO ≡ △CDO です。
合同な図形の対応する辺の長さが等しいことから、
AO = CO …(4)
BO = DO …(5)
(4) と (5) は、四角形ABCD の対角線がそれぞれの中点で交わっていることを示しています。【証明完了】
これで、「四角形ABCD が平行四辺形ならば、対角線がそれぞれの中点で交わる」ということが証明できました。
命題が真なので、
条件 p「平行四辺形である」ということが十分条件で、条件 q「対角線がそれぞれの中点で交わる」ということが必要条件となっています。
さらに、「平行四辺形ならば1組の向かい合う辺が等しく平行である」という命題も真だということが分かります。
平行四辺形だと①より、特に向かい合う1組の辺が平行ですし、②より、向かい合う1組の辺の長さが等しくなっています。
そのため、「平行四辺形ならば1組の向かい合う辺が等しく平行である」という命題も真で、「1組の向かい合う辺が等しく平行である」という条件も必要条件となっています。
ここから十分性の確認を行いますが、先に【図1】について議論をしてから、【図2】の「対角線がそれぞれの中点で交わる」について議論をするようにします。
逆も成立するとき
【命題2】
四角形ABCD について、
四角形ABCD の対角線がそれぞれの中点で交わるならば、四角形ABCD は平行四辺形である。
<証明>
対角線AC と BD を引き、それらの交点を O と置くことにします。
△ABO と △CDO について、合同となっていることを示します。
仮定より、対角線がそれぞれの中点で交わるため、
AO = CO,
BO = DO となっています。
また、対頂角は等しいので、
∠AOB = ∠COD です。
よって、2辺とその間の角がそれぞれ等しいため、△ABO と △CDO は合同です。
そのため、
AB = CD …(1)
△AOD と △COB についても、同様にして合同ということが示せます。
そのため、
AD = CB …(2)
(1), (2) より、四角形の向かい合う2組の辺がそれぞれ等しいため、四角形ABCD は平行四辺形です。【証明完了】
「四角形ABCD の対角線がそれぞれの中点で交わるならば、四角形ABCD は平行四辺形である」ということを示すことができました。
そのため、必要条件と十分条件は、必要十分条件ということになります。
平行四辺形という条件を満たす四角形全体を集合 A とし、対角線がそれぞれの中点で交わる四角形全体を集合 B とすると、A と B が一致しているという状況になっていました。
今度は、【図2】について、十分性の確認を行います。
つまり、「平行四辺形ならば1組の向かい合う辺が等しく平行である」という命題の逆も真であることを示します。
図2についても
四角形ABCD について、
AD = BC かつ AD//BC ならば、四角形ABCD は平行四辺形である。
<証明>
対角線AC と BD を引き、それらの交点を O と置くことにします。
△AOD と △COB について、
仮定より、
AD = CB …(1)
AD//BC なので、錯覚が等しいため、
∠ADO = ∠CBO …(2)
∠DAO = ∠BCO …(3)
(1), (2), (3) より、
1組の辺とその両端の角がそれぞれ等しいため、
△AOD と △COB は合同です。
そのため、
AO = CO …(4)
OD = OB …(5)
(4), (5) より、対角線がそれぞれの中点で交わっているため、【命題2】から四角形ABCD は平行四辺形です。【証明完了】
この証明のように、数学では既に証明した命題を適用することができます。
証明の最後の方で、先ほど証明した【命題2】を使いました。
平行四辺形となる条件は多いので、まとめておきます。
【平行四辺形となる条件】
次の①から⑤のうち1つでも成立すると平行四辺形である。
① 2組の向かい合う辺がそれぞれ平行である。
② 2組の向かい合う辺がそれぞれ等しい。
③ 2組の向かい合う角の大きさがそれぞれ等しい。
④ 対角線がそれぞれの中点で交わる。
⑤ 1組の向かい合う辺が等しく平行である。
この数学サイトで、大学の数学の証明を行うときも、必要条件-十分条件を意識しながら証明を行っています。
大学の内容だと、扱う内容が複雑ですが、論理の骨格自体は中学の数学の平行四辺形の内容と同じ論理と集合になります。
そのような論理や集合の扱いに慣れることを目的に、扱う対象を中学で学習する図形にし、論理の骨格に集中するということで今回の記事を投稿しました。
同じ趣旨で、長方形-定義という記事でも、長方形を使って論理や集合を意識する内容を解説しています。
また、四角形の対角線に関連して、
ひし形-定義という記事も投稿しています。
それでは、これで今回のタロウ岩井の記事を終了します。
読んで頂き、ありがとうございました。