方向ベクトル – 法線ベクトル | 直線の傾きmとx切片y切片をベクトル方程式で
" 方向ベクトル “と" 法線ベクトル “を直線のベクトル方程式の考え方で使えるようになると役に立ちます。
直線に関して、傾き m と x切片, y切片の値が、どのようにベクトル方程式とつながるのかを押さえることが理解への近道となります。
数学IIの直線を表す方程式と軌跡の考え方を、ベクトルを交えて発展させることが大切になります。
実数を使ってスカラー倍をすることで、ベクトルの長さを拡大縮小する、もしくは向きを逆転することができます。
スカラー倍を考慮して方向ベクトルの成分を扱いやすい値で議論を進めることがポイントになります。
方向ベクトル :変化の割合をベクトルで
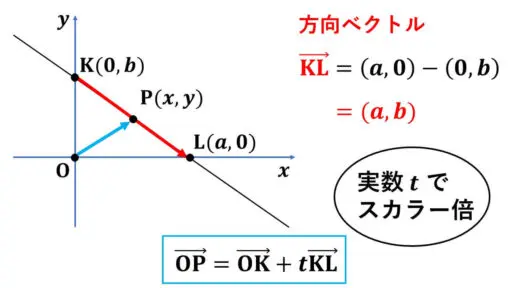
※ ただし、a ≠ 0, b ≠ 0 として、この記事の議論を進めることにします。
動く動点 P(x, y) について、軌跡の考え方で x と y を用いた関係式(等式)を導くことを考えます。
直線KL が点 K で y 軸と、点 L で x 軸で交わっているという状況から、図の下に記述している直線の方程式が得られます。
傾き m は変化の割合(平均変化率)のことで、y の増加量を x の増加量で割った値となります。
つまり、m = -b÷a です。
ベクトルOK が定ベクトルで、ベクトルKL が方向ベクトルです。
この方向ベクトルが傾きに相当します。
原点 O(0, 0) を位置ベクトルの基準として、点 K, L, P の位置ベクトルをそれぞれ k, l, p と表すことにします。
実数 t でスカラー倍をすることで調整することによって、
p = k+t(l-k) というベクトル方程式で、点 P の位置ベクトルを表すことができます。
l-k = (a, -b) が方向ベクトルの成分表示です。
y 成分の値を x 成分の値で割ると、
m = -b÷a という直線の変化の割合である傾きとなります。
ここで、点 P が動くので、実数 t を使って調整をしていることを考慮して、方向ベクトルの成分表示を扱いやすい値にすることを考えます。
d = (1, m) というベクトルは、x の増加量 1 に対して、y の増加量が m なので、変化の割合が同じ m です。
そのため、d は直線の方向ベクトルに平行です。
方向ベクトルの x 成分と y 成分は実数 t でスカラー倍をすることで調整されるので、d を使って直線のベクトル方程式を表すことができます。
p = k+td(ただし、t は実数)を直線KL のベクトル方程式として考えると、d の成分がシンプルなので、計算がしやすくなります。
このベクトル方程式ですが、左辺と右辺の x 成分と y 成分の値を比較することで、数学II で学習する直線を表す方程式が得られます。
x成分とy成分の比較と傾きm
p = (x, y), k = (0, b),
d = (1, m) だったので、
(x, y) = (0, b)+t(1, m)
= (t, b+tm) となっています。
x 成分を比較すると、
x = t です。
y 成分を比較すると、
y = b+tm です。
t = x なので、
y = mx+b となります。
傾き m で、y切片の値が b という数学II で扱う直線を表す方程式となっています。
m = -b÷a だったので、
両辺を a 倍すると、
ay = -bx+b となります。
移項すると、
bx+ay-b = 0 という直線を表す方程式の形になります。
数学II で扱われる直線の方程式が与えられたときに、y の係数を x 成分にし、x の係数の-1倍を y 成分とすると、
l-k = (a, -b) という、はじめに述べた方向ベクトルKL の成分表示となります。
このベクトルを 1/a でスカラー倍すると、
d = (1, -b/a) = (1, m) となります。
状況に応じて、d を方向ベクトルとして考えて直線のベクトル方程式の議論を進めることもできます。
ここからは、この直線KL に垂直な直線の傾きである法線ベクトルについて考えます。
方向ベクトル から 法線ベクトル
直線KL の傾き m = -b/a について、この直線KL と垂直に交わる直線の傾きは、すぐに計算で求めることができます。
二直線が垂直に交わるとき、傾きの積が -1 なので、直線KL に垂直な直線の傾きは、
-1/m = a/b です。
この垂直に交わる直線の傾きに相当するベクトルが法線ベクトル n です。
x の増加量 b に対して、y の増加量 a ということなので、
n = (b, a) です。
スカラー倍をしても平行なので、
(1, a/b) = (1, -1/m) を直線KL に垂直な直線の方向ベクトルとして考えることもできます。
垂直ということは、内積とも関連します。実際に内積を計算してみます。
垂直なことと内積
直線KL の方向ベクトルが、
(b, -a) でした。
直線KL に垂直な直線の方向ベクトルは、
(a, b) です。
垂直ということは、内積を計算すると 0 になります。
実際、
(b, -a)・(a, b)
= ba+(-ab) = 0 となっています。
※ 内積の定義についてはリンク先の記事で解説をしています。
ちなみに、直線KL と点 H(p, q) において垂直に交わる直線のベクトル方程式は、すぐに計算することができます。
直線KL の法線ベクトル (a, b) が、垂直に交わる直線の方向ベクトルとなっているので、次のように計算できます。
点 Q(x, y) を点 H で垂直に交わる直線上の点とします。
すると、
(x, y) = (p, q)+s(a, b)(ただし、s は実数)と表せます。
※ 数学IIの直線の方程式にしたいときは、x 成分と y 成分を比較して連立方程式を作り、パラメータ s を消去します。
では、ここまでの理論を、具体的な練習問題で実践してみます。
方向ベクトル-法線ベクトル:平行で実践練習
【練習問題1】
直線 3x+y-7 = 0 に平行で、
点 (6, -4) を通る直線の方程式を求めてください。
直線 3x+y-7 = 0 の方向ベクトルは、
(1, -3) です。
y の係数を x 成分にし、x の係数の-1倍を y 成分とすると方向ベクトルになるという理論を使いました。
求める直線は、平行だったので、方向ベクトルは同じです。
そのため、(1, -3) が求める直線の方向ベクトルです。
求める直線上の点を (x, y) とすると、
実数 t を用いて、
(x, y) = (6, -4)+t(1, -3) というベクトル方程式が得られます。
途中の考え方を記述しないマーク型の大学受験だと、難関大学を志望する場合は、ここまで 1 秒以内で考えられるようにしておくと良いかと思います。
成分を比較すると、
x = 6+t かつ、
y = -4-3t より、
y = -4-3(x-6) です。
すなわち、
3x+y-14 = 0 です。
今、方向ベクトルを使って、求めました。法線ベクトルを使うと、もっと速く直線の方程式を求めることができます。
マーク型では解くスピードを上げる
直線 3x+y-7 = 0 の方向ベクトルに垂直な法線ベクトルは、
n = (3, 1) です。
先ほど述べた法線ベクトルの内容から、x の係数を x 成分に、y の係数を y 成分とすると法線ベクトルになります。
点 (6, -4) を通る直線の方程式を求めたいわけです。
軌跡の発想から、(x, y) を求める直線上の点として、x と y を用いた関係式を作りたいわけです。
二点 (6, -4) と (x, y) が、求める直線上の点なので、
ベクトル (x-6, y+4) は法線ベクトルと垂直な関係となっています。
垂直ということは内積を計算した値が 0 です。
よって、
(3, 1)・(x-6, y+4) = 0 です。
すなわち、
3(x-6)+(y+4) = 0 です。
マーク型で難しい大学を志望するときには、ここまで 1 秒くらいです。
理論を理解して、実践練習をトレーニングをすると、
直線 3x+y-7 = 0 に平行で、
点 (6, -4) を通る直線の方程式を求めるときに、
3(x-6)+(y+4) = 0 が 1 秒以内に実現できます。
理論の理解と実践によって、計算ミスのリスクがある分数の計算を回避して、楽に、
3(x-6)+(y+4) = 0 が得られます。
展開して整理すると、
3x+y-14 = 0 です。
「共通テストなどで 数学IIB を制限時間の中で余裕をもって満点をとる」といったときには、速く正確に解ける理論の習得が大切になります。
表面的な解法の暗記だと、理論に振り回されてしまうので、この内容をまとめない方が良いかもしれないのですが、正しく理論を理解して使いこなせると強力なので、証明つきで「まとめ」ておきます。
役立つ直線のベクトル方程式
【理論1】
直線 ax+by+c = 0 に平行で、
定点 (p, q) を通る直線の方程式は、
a(x-p)+b(y-q) = 0 である。
<証明>
直線 ax+by+c = 0 に平行で、
定点 (p, q) を通る直線上の点を (x, y) とします。
ベクトル (x-p, y-q) は、
直線 ax+by+c = 0 の方向ベクトルと平行なので、
直線 ax+by+c = 0 の法線ベクトルに垂直です。
法線ベクトル (a, b) との内積値が 0 より、
(a, b)・(x-p, y-q) = 0
すなわち、
a(x-p)+b(y-q) = 0 です。【証明完了】
今度は、定点を通る垂直な直線の方程式を求める練習です。
方向ベクトル-法線ベクトル:垂直で実践練習
【練習問題2】
直線 x-5y+2 = 0 に垂直で、
点 (-1, 3) を通る直線の方程式を求めてください。
直線 x-5y+2 = 0 に垂直で、
点 (-1, 3) を通る直線上の点を (x, y) とします。
ベクトル (x+1, y-3) は、
(-5, -1) という直線 x-5y+2 = 0 の方向ベクトルに垂直です。
よって、
(-5, -1)・(x+1, y-3) = 0 です。
そのため、
-5(x+1)-(y-3) = 0
つまり、
-5x-y-2 = 0 が求める直線の方程式です。
垂直についても、まとめておきます。
役立つ理論-垂直編
【理論2】
直線 ax+by+c = 0 に垂直で、
定点 (p, q) を通る直線の方程式は、
b(x-p)-a(y-q) = 0 である。
<証明>
直線 ax+by+c = 0 に垂直で、
定点 (p, q) を通る直線上の点を (x, y) とします。
ベクトル (x-p, y-q) は、
直線 ax+by+c = 0 の方向ベクトルと垂直です。
直線 ax+by+c = 0 の方向ベクトルは
(b, -a) です。
直交するベクトルの内積値は 0 なので、
(b, -a)・(x-p, y-q) = 0
つまり、
b(x-p)-a(y-q) = 0 が求める直線の方程式です。【証明完了】
マーク式だと、ここまでの証明の内容を記述しなくて良いため、考えるだけなので約 1 秒です。
【理論1】と【理論2】が二つあるので、理論を理解して実践練習を通じて自分のものにしておかないと、表面的な暗記だと、入試の本番で肝心なときに使えないことになってしまいます。
しかし、地に足をつけて、軌跡やベクトルの理解を基礎として、これらの理論を理解して使えるようになっておくと、分数の計算やルートが絡んだり、文字だけだったりという場面で、速く正確に方程式が求まります。
関連する内容として、円の接線という記事中心が原点ではない円の接線の方程式の求め方を解説しています。
原点と接点を結んだベクトルが接線の方向ベクトルと垂直ということが決め手になります。
また、数IIの点と直線の距離の公式を導くのにも、方向ベクトルと法線ベクトルの考え方が有効です。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。