底の変換公式の証明 | 定義に基づいて証明をし、理解をしたら例題を用いて使い方を確認[log]

2023年5月6日

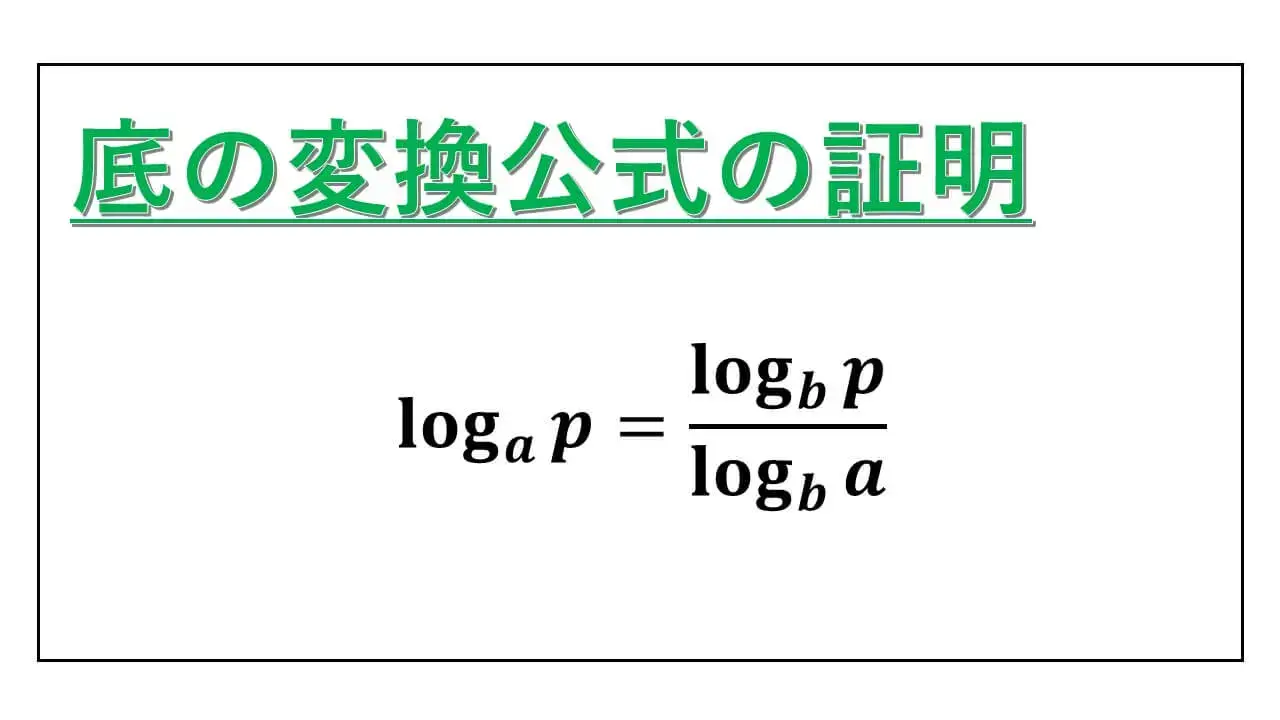
" 底の変換公式の証明 “を理解するで、対数関数の底の変換に慣れることができます。

文字を使った状態で、底の変換の仕組みを理解しておくと、紛らわしい内容のときでも、自分で考えて推論を進めることができます。

そのため、まずは底の変換公式の証明を理解することから学習を始めると良いかと思います。

その後で、具体的な数字を用いた問題で、底の変換の練習をすると、しっかりと身につきます。

底と真数の関係を意識しながら、定義に基づいて対数関数を考えることに慣れておくと、指数関数と合わせて、スムーズに理解できると思います。

まず、真数と底についての関係を復習しながら、対数についての公式を証明してみます。

良い定義の復習になり、底の変換公式を証明するための準備運動になります。

対数の単元で、よく使う公式を証明し、その後で、底の変換公式の証明へと向かいます。

y = a^x (a > 0, a ≠ 1)について、
a^s = a^t だと s = t となるという指数関数の単調性を利用して推論を進めます。

底の変換公式 :定義の確認から

a を 0 より大きい 1 ではない実数とします。そして、b を 0 より大きい実数とします。

このとき、log_ab は、実数です。

実数なので、log_ab = c と置いておきます。

この c は、底と真数についての対数の定義から、
a^c = b となります。

この定義に基づいて、次の公式を証明します。この内容を理解することで、底の変換公式の内容の理解へとつながります。

指数法則の利用

次の三つの公式では、
p, q は正の実数とし、r は実数です。

・log_apq = log_ap + log_aq

・log_ap/q = log_ap － log_aq

・log_ap^r = rlog_ap

まず、一番上の等式から証明します。

log_ap = c, log_aq = d と置きます。

真数と底の関係から、
a^c = p, a^d = q です。

ここで、a^c × a^d = a^c+d です。

この指数法則から、
a^c+d = a^c × a^d = pq

よって、底と真数の関係より ax = pq を満たす実数 x は、log_apq ただ一つなので、
log_apq = c + d となります。

※ 指数関数 y = a^x の単調性です。

c と d を元に戻すと、
log_apq = log_ap + log_aq

これで、一つ目の公式が証明できました。

同じ要領で、
log_ap = c, log_aq = d と置き、
log_ap/q = log_ap － log_aq を証明します。

a^c ÷ a^d = a^c-d より p/q = a^c-d

底と真数の関係から、
log_ap/q = c － d です。

c, d を元に戻すと、
log_ap/q = log_ap － log_aq

また、a^c = p より、
両辺を r 乗すると、(a^c)^r = p^r

(a^c)^r = a^cr = a^rc より、a^rc = p^r

よって、
ax = pr を満たす x は、
log_ap^r ただ一つなので、
log_ap^r = rc = rlog_ap【証明完了】

これで、三つの等式を証明できました。

ここまでで述べた内容を基に、底の変換公式を考察します。

底の変換公式 :メインの公式の証明

先ほど、三つの等式を証明しました。証明のポイントは、指数関数の単調性（単射性）です。

a^x = a^y となっていたときに、x = y ということを使いました。

底の変換公式の証明も、この指数関数の単調性を使います。

それでは、底の変換公式を証明します。

他の文字で置く

log_ap = s, log_bp = t,
log_ba = r と置きます。

底と真数の関係から、
a^s = p, b^t = p, b^r = a

今、a^s = b^t となっているので、
b^r = a を代入すると、(b^r)^s = b^t

つまり、b^rs = b^t

よって、指数関数 y = b^x の単調性から、
rs = t です。

元の文字に戻すと、
log_ba × log_ap = log_bp

log_ba ≠ 0 より、
log_ap = log_bp ÷ log_ba【証明完了】

指数関数の単調性が効きました。

単射ということを高校の数学から意識すると、大学の数学で、全単射をよく使うので、良いかと思います。

それでは、具体的な数字を用いて、底の変換公式を練習します。「底をそろえる」が、よく式を書き換えるときのポイントになります。

具体例で練習

【練習問題】

log₂3 + log₄27 の底をそろえてください。

底の変換公式を使うと、
log₄27 = log₂27 ÷ log₂4

ここで、
log₂27 = log₂3³ = 3log₂3,
log₂4 = log₂2² = 2log₂2 = 2 です。
※ 2¹ = 2 より log₂2 = 1 です。

よって、

log₂3 + log₄25 =
log₂3 + 3log₂3 ÷ 2
= log₂3 + 3/2 × log₂3
= (1+3/2)× log₂3 = 5/2 × log₂3

このように、底の変換公式を使って、底をそろえると、うまく計算できるときが多いです。

最後に、底の変換公式と合わせて、対数関数の単調性について述べておきます。底をそろえることで、大小関係が分かるときがあります。

底の変換公式 :対数関数の単調性

a > 1 のとき、
y = log_ax は、単調増加関数です。

つまり、
0 < s < t のとき、log_as < log_at

また、0 < a < 1 のとき、
y = log_ax は単調減少関数です。

つまり、
0 < s < t のとき、log_as > log_at

この単調性を利用して、対数関数の値の大小関係を考察する練習問題を扱ってみます。

底の変換公式で、底を変換することで、単調性を使えるようにします。

練習問題

log₃4, log₄3 という二つの実数について、大小関係を考えてください。

ここで、3^1/2 はルート 3 のことで、
約 1.732 なので、2 より小さい実数です。

そのため、
log₄3 = log₂3^1/2 < log₂2 = 1

底をそろえることで、対数関数の単調性が使えて、大小関係が明確になりました。

※ 慣れている方にとっては、底の変換公式を使わなくても、1 より小さい値ということが分かりますが、敢えて練習に変換公式を使いました。

一方、1 = log₃3 < log₃4 です。

よって、
log₄3 < 1 より、log₄3 < log₃4

1 を境目に、大小関係を考察できました。

a > 0, a ≠ 1 のとき、log_aa = 1 なので、
log₂2 = 1 = log₃3 を境として、大小関係を比較しました。

ルートを取るということは、1/2乗するということも、よく使います。

数学２を学習するようになると、二重根号の外し方を敢えて1/2乗という指数が分数のときで考えるのも良い練習になるかと思います。

関連記事として、二重根号の外し方についての記事へのリンクを置いておきます。

指数についての基礎的な内容は、
指数方程式という記事で解説をしています。

合わせて対数方程式という記事も投稿しています。

数学２を学習するときに、指数・対数と並んで三角関数の式の書き換えは大切になります。

指数と対数については、底と真数の関係、そして関数の単調性が大切になります。

一方、三角関数の式の書き換えでは、加法定理が基本になります。

その意味で、和積変換公式の証明の記事を置いておきます。

底の変換公式のように、公式の証明を理解することで、公式を使うための基礎となる素養が磨かれるかと思います。

数IIの対数については、
常用対数という底 10 の対数について解説をしています。

これで今回のブログを終了します。

読んで頂き、ありがとうございました。