同じものを含む順列 – 最短経路問題 | 何通りかを考える

2023年10月5日

" 同じものを含む順列 “に関して、" 最短経路問題 “を高校一年の数学で学習します。

最短の経路が何通りあるのかを求めるときに、順列が何通りあるのかを計算する公式を同じものが含まれているということで修正する必要があります。

異なる n 個もので順列を考えると n! 通りですが、n 個の中に同じものが含まれているときに、どうするのか。

何通りあるのかを数えるという観点から、越えるべき壁にどう対処するのかを解説します。

最短経路の問題を解くために使う同じものを含む順列の数え方から説明します。

同じものを含む順列 :最短経路問題への準備

最短経路の問題を解くためには、基礎となる理論を押さえることが大切になります。

基礎をしっかりと築き足場を固めるところからスタートします。

この基礎となるのが「同じものを含む順列」の数え方です。

抽象的な証明もできるのですが、具体的な状況で、着実に数えられるようにすることに焦点を当て、難しい公式の証明をしないことにします。

実は、同じものを含む順列が何通りあるのかということを示すためには組合せの発想を使いまして、組合せの公式については、リンク先の記事で大学の数学を使って厳密証明をしています。

同じものを含む順列の公式の厳密な証明はしませんが、その考え方自体は、具体的に数えながら伝えるようにしています。

具体的に数える練習

【同じものを含む順列の例】

JAPAN に使われている 5 つの文字を並び替えた順列が何通りあるのかを数えます。

英語の意味は気にせず、J, A, P, A, N の 5 つの文字を一列に並べて順列を可能な限り作ります。

このときに、順列が全部で何通りできるのかを考えます。

A と A が区別のない文字なので、異なる 5 つを並べるという公式がストレートに使えない状況です。

5 つの文字が異なっていると順列の総数を求める公式が使えるという状況でもあります。

そこで、A₁, A₂ と番号をつけて一旦は区別をします。

JA₁PA₂N だと異なる 5 つの文字なので、順列の総数が何通りかを計算することができます。

5! = 5・4・3・2・1
= 120 （通り）

とりあえず区別をして 120 通りと仮に数えておきます。

この 120 通りの中には、
JA₁PA₂N と JA₂PA₁N が、それぞれ区別されて、どちらも 1 通りとしてカウントされ、120 通りの中の 2 通りとなっています。

ここで、区別をなくします。

すると、JAPAN と JAPAN は同じなので、1 通りです。

つまり、120 通りの順列の中で、A₁ と A₂ だけが入れ替わっていて、他の文字の並びが同じものが 1 つに集約されます。

A₁ と A₂ の入れ替え方は、2! なので、区別のない 2 つの文字を含んだ 5 つの文字の並べ方は、次のように計算できます。

5! ÷ 2! = 120 ÷ 2
= 60 （通り）

この計算をよく見ると、
(5・4 ÷ 2!) × 3! です。

5・4 ÷ 2! は、₅C₂ という組合せの公式です。

上の内容を組合せを使って考えることができるということも分かります。

□□□□□ という 5 つの箇所から、はじめに区別のない A を置く位置を指定します。

□A□□A□ というように 5 ヵ所から A を置く 2 ヵ所の位置を選ぶ方法は、組合せを使って計算できます。

₅C₂ 通りが、区別のない A を置く 2 ヵ所の選び方です。

□A□□A□ のように 2 つの A を置くと、残りの 3 ヵ所に異なる 3 つの文字を置くことになります。

異なる 3 つの文字を異なる 3 ヵ所に並べるので、3! 通りの並べ方と分かります。

樹形図の発想で積の法則を使うと、
全部で ₅C₂ × 3! 通りとなります。

計算をすると、
5! ÷ 2! と同じ値になっています。

最短経路の問題を解く前に、もう少し同じものを含む順列の数え方を練習しておきます。

より複雑な順列で練習

【同じものを含む順列の例２】

NIPPON に使われている 6 つの文字を並び替えた順列が何通りあるのかを数えます。

区別のない N が 2 個、区別のない P が 2 個あります。

先ほどの組合せの発想で攻めます。

□□□□□□ という 6 ヵ所から、まず N を配置する 2 ヵ所を選びます。

₆C₂ 通りの選び方があります。

この ₆C₂ の一つは、例えば、
□N□□N□ というようになっています。

このように、4 ヵ所の □ が残っています。

この 4 ヵ所から、2 つの区別のない P を配置する 2 ヵ所を選びます。

₄C₂ 通りの選び方があります。

これで、区別のない 4 個の文字を配置する位置を選びました。

全部で、₆C₂・₄C₂ 通りの区別のない文字の配置する位置が決めりました。

そのうちの一つは、例えば、
□NP□NP というような形です。

₆C₂・₄C₂ 通りのそれぞれについて、残った 2 つの □ の位置に I と O を配置します。

異なる 2 個を 2 ヵ所に並べるので、2! 通りです。

樹形図の発想で積の法則を使うと、
₆C₂・₄C₂ × 3! 通りとなります。

これが求める場合の総数です。

このように、組合せの考え方で、区別のない文字の配置先を決定しておいてから、残りの位置に異なる残りの文字を並べるという数え方です。

この考え方で、最短経路の問題の経路を数えます。

最短経路 :問題を実践練習

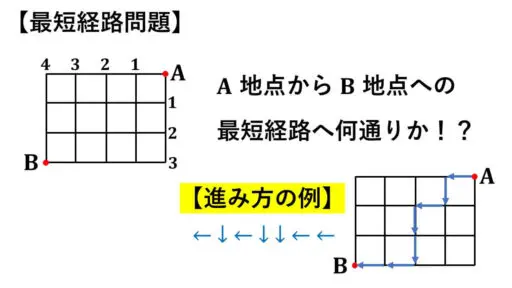
最短というくらいで、戻らずに進む移動になります。

そのため、A 地点から B 地点への移動は、← と ↓ しか選択肢がありません。

↑ や → の方向へ移動してしまうと、戻ってしまうので、最短経路の移動としては← と ↓ しか移動する方向を考えません。

この最短経路は、上の例に示しているようにデジタルな考え方になります。

←↓←↓↓←← と 7 ヵ所に ← や ↓ を並べると、1 通りの最短経路の移動となります。

4 つの ← と 3 つの ↓ を 7 ヵ所に配置する並べ方の総数が、最短経路の移動の総数となります。

つまり、同じものを含む順列が何通りあるのかということになります。

では、A 地点から B 地点への最短経路の移動が全部で何通りあるのかを数えます。

最短経路の移動が何通りか

7 つの矢印を 7 ヵ所に並べるのですが、4 つの ← は区別がありません。

そして、3 つの ↓ も区別がありません。

そこで、7 ヵ所から、4 つの ← を配置する 4 ヵ所を選びます。

₇C₄ 通りの組合せです。

この組合せの一つ一つについて、それぞれ 3 ヵ所が残っています。

その 3 ヵ所に区別のない 3 つの ↓ を配置します。

区別のないものを配置する場所を選ぶのは組合せを計算します。

₃C₃ 通りです。

これで、7 ヵ所が全て埋まりました。

全部で ₇C₃・₃C₃ 通りです。

₃C₃ = 1 なので、計算するのは ₇C₃ だけです。

(7・6・5) ÷ (3・2・1)
= (7・6・5) ÷ 6
= 7・5 = 35 （通り）

これで、求める最短経路の移動が 35 通りと分かりました。

このように、区別のない同じものを含む順列の総数の数え方の基礎を組合せで理解をしておくと、最短経路のような難しそうな内容でも、考えて求めることができます。

場合の数、確率の単元の基礎となる内容は、扱う内容が長いので、息切れせずに、基礎となる内容たちをしっかりと理解して使いこなせるようになることが大切かと思います。

区別について

今回は、区別のない同じものを含む順列の考え方で、最短経路が何通りかを数えました。

要素の個数については、個数定理という記事を投稿しています。

ただ、高校数学で、区別のないものを、どのように処理するのかということについて、確率を定義するために理論上の区別をするというときがあります。

確率を定義するときには、同様に確からしいということが前提になります。

この同様な確からしさとの関わりから、区別のないものだけど、番号をつけるなどして区別するときがあります。

最後に、同じものを含む順列について、最短経路とは別の思考力を使う問題を１つ扱っておきます。

同じものを含む順列 :難しい問題

【問題】

1, 2, 3, 4, 5 の中から重複を許して 6 個の数字を選び一列に並べた順列を考えます。

このような順列のうち、どの数字もそれ以外の数字のどれかに等しくなっているものが全部で何通りあるかを求めてください。

1, 2, 3, 4, 5 の中から重複を許して 6 個の数字を選び一列に並べた順列は、重複順列で、全部で5⁶通りあります。

この5⁶通りの重複順列の中で、どの数字もそれ以外の数字のどれかに等しくなっているという条件を満たすものが何通りあるのかという問題になります。

例えば、
125512 だと、条件を満たしているので１通りとカウントされるわけです。

場合が何通りあるのかの計算をする前に、条件をみたす順列はどうなっているのかということを考察しないと数えあげるのが困難です。

まずは、どの数字もそれ以外の数字のどれかに等しくなっている順列が、どういったタイプなのかを考えます。

まずはじめに目をつけるのが、重複を認めて選んだ 6 個の数字の中で、相異なる数字が最大で何種類あるのかということになります。

125512だと、相異なる数字は 1, 2, 5 の 3 種類です。

どの数字もそれ以外の数字のどれかに等しくなっているという条件を満たす 6 個の数字から成る順列なので、相異なる数字は 4 種類以上になることは起こり得ないということが分かります。

そのため、相異なる数字は最大で 3 種類ということになります。

最大で 3 種類しかないということが分かると、場合分けて、起こり得る可能性をすべて見切ってしまうことができます。

そこで、相異なる数字が 2 種類のときと、1 種類のときについても、さらに考察します。

条件をより細かく考察

相異なる数字が 2 種類のときについて考えます。

例えば、2 種類の数字が 1 と 4 だったとしてシミュレーションしてみます。

144414 というように、1 種類の数字が 2 個重複、もう 1 種類の数字が 4 個重複するという場合があります。

このように、条件をより細かく絞るために、重複する個数に注目することができます。

他の可能性として、1 種類の数字が 3 個重複し、必然的にもう 1 種類の数字も 3 個重複するということが考えられます。

例えば、141414 というものです。

これくらいまで考察が進むと、同じものを含む順列の考え方で計算ができるという見通しがたちます。

そのため、1 種類の数字が 4 個重複し、もう 1 種類の数字が 2 個重複するという場合は、すでに考察した内容と同じということが分かります。

これで、相異なる数字が 2 種類のときについての起こり得る分岐は全て見切れました。

残すは、相異なる数字が 1 種類のときについてです。

このときは、6 個の順列が全て同じというタイプになります。

例えば、111111 や 555555 という単純なものたちです。

これで、「どの数字もそれ以外の数字のどれかに等しくなっている」の全ての分岐が分かりました。

それらをまとめておきます。

これら 4 つのタイプを同じものを含む順列の考え方で計算し、すべてを合計すると求めたい通りが何通りかということが分かります。

それぞれの場合を計算

「① 相異なる数字が3種類」が何通りかということから計算をします。

これは、●2個、▼2個、■2個という同じものを含む 6 個の記号から成る順列です。

これらの順列は、
6!/2!2!2! なので、
90 通りです。

さらに、●、▼、■のそれぞれには、1, 2, 3, 4, 5 の中から選んだ数字が登場します。

今、3 種類が相異なる数字という状況で考えているので、1, 2, 3, 4, 5 の中から異なる 3 個の数字を選ぶということになります。

そのため、₅C₃ = 10 通りが●、▼、■の所へ配置される可能性になります。

よって、①のタイプの順列は、
10×90 = 900 通りと分かりました。

●2個、▼2個、■2個という状況なので、₅P₃ としてしまうと、同じ順列をダブって数えてしまうことになります。

そのため、₅P₃÷3! = ₅C₃ = 10 で計算をすることになりました。

今度は、「② 相異なる数字が2種類で、1種類が2個重複し、もう1種類が4個重複する」というタイプの順列が何通りかを計算します。

●2個、■4個から成る同じものを含む順列で、
5 個の数字から選んだ数字を●と■の 2 か所に並べるわけです。

よって、
₅P₂×6!/2!4!
= 20×15
= 300 通りです。

「③ 相異なる数字が2種類で、1種類が3個重複し、もう1種類も3個重複する」というタイプの順列が何通りかを計算するときには注意です。

●3個、■3個から成る同じものを含む順列で、
5 個の数字から選んだ数字を●と■の 2 か所に並べるわけですが、●も■も同じ 3 個なので、選んだ 2 個の数字のどちらを●に配置しても、順列の総数としては同じになってしまいます。

そのため、₅P₂÷2 となります。

この÷2が、②のタイプと③のタイプのちがいになります。

(₅P₂÷2)×6!/3!3!
= ₅C₂×6!/3!3!
= 10×20
= 200 通りになります。

1, 2, 3, 4, 5 の中から数字を 2 個選び、2 個のうち、どちらを●に配置しても、●3個と■3個の順列の総数を考えたときにダブりが起きてしまうため、÷2をするというわけです。

このため、①のタイプと③のタイプは÷3!や÷2!をするということになります。

「④ 相異なる数字が1種類」は、計算しなくても書き出すことができるほどシンプルです。

111111, 222222,
333333, 444444,
555555 の 5通りになります。

敢えて式を述べると、
1,2,3,4,5 の中から数字を 1 つ選び、その選んだ数字を 6 個並べるので、
₅C₁ = 5 通りです。

すべてを合計する

①から④のタイプは、どの2つも共通の所が空となっている互いに素な事象ということになります。

そのため、上で計算したそれぞれの順列の個数を合計すると、求めたい順列の個数となります。

900+300+200+5
= 1405 通りです。

これが、どの数字もそれ以外の数字のどれかに等しくなっているという条件を満たす順列の総数になります。

最後に大学受験レベルの問題を扱いましたが、
期待値のような高校数学の基礎的な記事も投稿しています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。