論理記号 集合 | ∀(任意の)と∃(存在する) の使い方と意味を解説【大学数学の基礎】
" 論理記号 集合 ∀ ∃ “の使い方と意味の理解は、大学の数学を学習するときに必要です。
そこで、よく使われる集合についての内容を証明することで、論理記号の使い方と意味の理解を深めることができるかと思います。
既に知っている集合についての内容を用いて、論理記号について解説します。
「任意の」と「存在する」について、集合と合わせて基本を押さえることが大切になります。
論理記号 集合
∀（任意の）と∃（存在する）について、これから解説をします。
「任意の■について～が成立する」というような表現が、数学で使われます。
日常会話では、まず使われない表現なので、慣れるまで戸惑うことがあるかと思います。
しかし、議論の対象となる範囲が何かということを意識することは、大切になります。
この範囲を表しているのが、集合です。
∀や∃を考えるときに、どの集合の範囲内で議論をしているのかということを把握することが基本となります。
それでは、高校の数学で見たことがある内容を使って、∀から解説します。
全称記号∀
【部分集合の定義】
集合 S の任意の元（要素）が、集合 T の元であるとき、S を T の部分集合という。
要素（元）より
S ⊂ T という部分集合の定義に、「任意の」が使われています。論理記号を使うと次のようになります。
∀a ∈ S に対して a ∈ T であるとき、S を T の部分集合という。
∀a ∈ S は、集合 S という範囲内のどんな元 a についても以下のことが成立するということを表しています。
＜具体例＞
S = {1, 2, 3} とします。
∀a ∈ S に対して、a < 5 である。
真偽が明確に判断できる命題を例として挙げました。
この命題は真です。
論理記号の表す内容は、「任意の a ∈ S に対して、a は 5 より小さい」ということです。
集合 S の範囲内の元は、1 と 2 と 3 で、どれも 5 より小さいので、正しい命題です。
全称記号を使った命題は、一つでも範囲としている集合の元で満たさないものがあれば、偽となります。
※ この満たさない例を反例といいます。
※ 命題-仮定-結論というブログに高校で習う命題について解説をしています。
「∀a ∈ S に対して、a ≧ 2 である」という命題は偽です。1 ∈ S は 2 以上という条件を満たしていない S の元なので、反例となっています。
次に、シンプルな例を用いて、存在記号を解説します。
存在記号∃
＜具体例＞
S = {1, 2, 3, 6} とする。
∃a ∈ S such that 「a は 3 の倍数」。
∃a ∈ S such that 「～」は、「～」を満たす S の元が少なくとも 1 つ存在するという意味です。
such that 「～」は、（～を満たすような ）という意味です。「3 の倍数であるような S の元 a が存在する」という内容を表している具体例です。
少なくとも 1 つ存在するということなので、複数のものが存在するということが起きるときもあります。
この例だと、3 ∈ S と 6 ∈ S は、どちらも 3 の倍数です。このように、条件を満たすものが複数存在するときもあるので注意です。
ちなみに、条件を満たすものが唯一であるときには、一意的に存在するといいます。
論理記号 集合 :∀や∃の否定
ここからは、否定について、∀や∃をどのように扱うのかを解説します。
これについては、一般的な扱い方を押さえてから例で確認するという流れが分かりやすいかと思います。
∀a ∈ S に対して「～」が成立する
これを否定することを考えます。
論理記号の意味は、『どんな a ∈ S に対しても「～」が成立する』ということです。
この内容を否定すると、『ある a ∈ S が存在して「～」が成立しない』ということになります。
これを論理記号で表すと、
∃a ∈ S such that ～が成立しない
となります。
【まとめ１】
「∀a ∈ S に対して「～」が成立する」の否定は、
「∃a ∈ S such that ～が成立しない」
「成立する」と「成立しない」は、否定をとると逆転します。
このことと合わせて、∀と∃も逆転させます。機械的に否定が作れるので、便利です。
もう一つ否定のパターンをまとめておきます。
【まとめ２】
「∃a ∈ S such that ～が成立する」の否定は、
「∀a ∈ S に対して「～」が成立しない」
【まとめ１】や【まとめ２】の「成立する」や「成立しない」を逆点させて、他のタイプも作れます。
【まとめ１’】
「∀a ∈ S に対して「～」が成立しない」の否定は、「∃a ∈ S such that ～が成立する」
【まとめ２’】
「∃a ∈ S such that ～が成立しない」の否定は、「∀a ∈ S に対して「～」が成立する」
命題の証明で、背理法を使ったり、対偶命題を考えるときに、論理記号も合わせて調整をします。
シンプルな例を使って、もう少し練習をしてみます。
否定の練習
【問題】
X を整数全体 Z の部分集合とし、S を 3 の倍数全体とします。
このとき、「∀a ∈ S に対して a は X の元ではない」の否定を考えてください。
「∀a ∈ S に対して a は X の元ではない」ということは、S に含まれているどんな元も X の元ではないということです。
この内容を否定すると、「ある S の元 a が存在して、a は X の元である」ということになります。
論理記号を使って表すと、
∃a ∈ S such that a ∈ X となります。
論理記号の使い方や意味自体は、シンプルな例で考えると、難しいものではないかと思います。
ただ、大学の数学の難しさは、扱う内容が高校のときに比べると、複雑になっています。そのために、内容が難しく思えることが多いかと思います。
次の内容は、数学科でよく使う集合の内容です。しかし、証明を述べると、結構な長さになります。論理の練習をするのに、適宜、集合で包含関係を考えると良いかと思います。
論理記号 集合 :包含関係を確認
A ∩ (B ∩ C) = (A ∩ B) ∩ C と、共通部分をとるということについての結合律が成立します。
この内容を定義に基づいて、論理的に証明をします。
【二つの集合が等しい定義】
集合 S と T について、
S ⊂ T かつ T ⊂ S であるとき、
S = T とする。
左辺の集合が右辺の集合の部分集合であり、かつ、右辺の集合が左辺の集合の部分集合であることを確認します。
A∩(B∩C)⊂(A∩B)∩Cの確認
∀a ∈ A ∩ (B ∩ C) に対し、共通部分の定義から、a ∈ A かつ a ∈ B ∩ C
さらに、B ∩ C の定義から、
a ∈ B かつ a ∈ C となっています。
したがって、a ∈ A ∩ B です。
a ∈ C も成立していたので、合わせて、
a ∈ (A ∩ B) ∩ C です。
ゆえに、部分集合の定義から、
A ∩ (B ∩ C) ⊂ (A ∩ B) ∩ C が示せました。
今度は、逆向きの包含関係を証明します。
(A∩B)∩C⊂A∩(B∩C)の確認
∀a ∈ (A ∩ B) ∩ C に対して、共通部分の定義から、a ∈ A ∩ B かつ a ∈ C となります。
A ∩ B の定義から、
a ∈ A かつ a ∈ B となっています。
今、a ∈ B かつ a ∈ C が成立しているので、
a ∈ B ∩ C です。
a ∈ A でもあるため、a ∈ A ∩ (B ∩ C)
よって、部分集合の定義から、
(A ∩ B) ∩ C ⊂ A ∩ (B ∩ C) です。
以上より、
A ∩ (B ∩ C) ⊂ (A ∩ B) ∩ C であり、
(A ∩ B) ∩ C ⊂ A ∩ (B ∩ C) でもあることが示せました。
二つの集合が等しいことの定義から、
A ∩ (B ∩ C) = (A ∩ B) ∩ C を証明できました。
これで、共通部分をとるということについて、結合法則が成立することが証明できました。
和集合「∪」についての結合法則は、
分配法則という記事の最後の部分で、証明を述べています。
元が集合に含まれているかどうかの判断を加えて、多くの数学の分野で集合の包含関係を考えます。数学の論理と一緒に、集合という範囲を意識すると、数学の理解が深まるかと思います。
関連する内容
今回のブログ記事で論理記号について解説しました。集合について、添え字が動く範囲となる添数集合の各元に対応する集合という発想も大切になります。
Λ ∋ λ について、Sλ という集合が対応するという表し方をよくします。
これも、高校の数学を例に、具体的に見ると、内容がすぐに分かります。
＜具体例＞
Λ = {2, 3, 4} とする。
このとき、λ ∈ Λ に対して、Sλ を整数 λ の倍数全体とする。
この例だと、2 という整数が添え字のとる値の一つで、S2 という集合が対応しています。
この S2 は、2 の倍数全体から成ります。
同じく、3 という添え字の値に対して、S3 という 3 の倍数全体が対応しています。4 には、4 の倍数全体、S4 が対応です。
先ほどのように、A, B, C と異なる集合をアルファベットで表すと、無限個の集合を表すことができません。
しかし、添数集合 Λ との対応だと、Λ が無限集合のときも対応する集合を考えることができます。
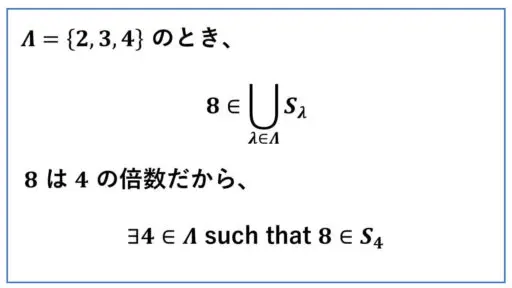
Λ = {2, 3, 4} のとき、
∪λSλ = S1 ∪ S2 ∪ S3 と 3 個の集合たちの和集合です。
もし、Λ が無限集合だとしても、無限個の集合の和集合を同じ記号で表せます。
a ∈ ∪λSλ で、a が和集合に含まれている元ということを表します。
ちなみに、和集合の元ということの定義に、論理記号が使われます。
「∃μ ∈ Λ such that a ∈ Sμ」というのが、a が和集合の元ということの定義です。
難しそうですが、先ほどの 3 個の例で確認をすると内容が分かりやすいです。
上で述べた内容ですが、存在するといったときに、複数の可能性が起こることもありました。
8 は 2 の倍数でもあるので、
∃2 ∈ Λ such that 8 ∈ S2
この例だと、8 を含む集合が 2 つ存在しています。
添数集合 Λ と、それに対応する集合という発想は、選択公理の内容で、無限個の集合の直積の定義を理解するために必要になります。
選択公理の記事で、集合論の入門的な内容について、無限個の集合の直積について解説をしています。
また、代数学の二項演算を考える例として、トーラス（円環）という記事を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。