連立不等式 | 「かつ」や「または」についての論理と同値な書き換えについて解説【高校の数学内容】
" 連立不等式 “を解くときに、論理を使うことが多いです。
もちろん、数直線やグラフを使った方が解きやすい問題もあるのですが、そういった図形的なアプローチを使わずに、単純に論理を使えるようになりたいという方の悩みを解消することを目指して今回の記事を投稿しました。
高校の数学にもなると、「かつ」や「または」を使って、論理的に考えることや同値な内容で書き換えるということをするときがあります。
連立不等式の内容について、論理についての解説に焦点を当てて、その運用方法を解説します。
大学受験の問題でも、明らかに論理を使って解くことを主眼として作られた問題も見ますので、論理を用いた考察で、連立不等式を解くことを解説します。
連立不等式 :同値な内容で書き換える
連立不等式の内容を考えるときに、同値な内容で書き換えるという数学で頻繁に使う手について述べておきます。
この内容は、あらゆる単元でよく使われるので、早い学習段階から認識ができると、内容をしっかりと理解することの手助けとなってくれます。
「p ならば q」が成立し、なおかつ「q ならば p」も成立しているとき、p が成立することと、q が成立することは同値であるといいます。
条件 p と条件 q が同値であるとき、書き換えをすることができます。
条件 p を満たすということは、同値である条件 q を満たすということと同じと考えます。
そのため、「条件 p を満たす」ということを「条件 q を満たす」と書き換えるときがあります。
数学では、同値な条件を、この書き換えをすることで、状況に応じて扱いやすい方で議論を進めることができます。
一般論を述べましたが、具体的な不等式を用いて、同値な書き換えについての理解を深められるように説明をします。
文字 x についての連立不等式というものは、x についての複数の不等式が与えられているものです。
不等式を満たすということが、不等式が定めている条件を満たすということです。
こういったことから、必然的に「かつ」や「または」といった論理の運用が関連してきます。
さらに、同値な書き換えも使うので、「かつ」や「または」に先立って、同値な書き換えについて解説をします。
不等式を同値に書き換える
実数 x は、
x－3 > 2 … (1) を満たすとします。
この (1) によって表される x の範囲が、x についての条件 p です。
(1) の範囲である x についての条件を満たすということを、x についての条件で、条件 p について同値な条件で書き換えることができるという例について説明をします。
x > 5 … (2) を x についての条件 q とします。
このとき、条件 p と、条件 q が同値となります。
同値というのは、「実数 x が条件 p を満たす」ならば、「実数 x が条件 q を満たす」ということが成立し、さらに、その逆も成立するということです。
「実数 x が条件 p を満たす」ならば、「実数 x が条件 q を満たす」ということを成立させる根拠は、不等式の性質です。
不等式の両辺に同じ実数を加えても、不等号の向きが変わらないという不等式の性質があります。
そのため、
x－3 < 2 が成立しているとするならば、
両辺に 3 を加えると、
(x－3)+3 < 2+3 が成立するということになります。
左辺は、x と同じ値なので、
x < 5 が成立している（実数 x は、条件 q を満たす）ということになります。
「実数 x が条件 q を満たす」ならば、「実数 x が条件 p を満たす」という逆も、不等式の性質から成立します。
不等式の性質で、両辺から同じ数を引いても、不等号の向きが変わらないということを用います。
そのため、「実数 x が条件 q を満たす」ということが成立しているとき、
x < 5 の両辺から 3 を引くことで、
x－3 < 2 が成立しているということになります。
つまり、「実数 x が条件 p を満たす」ということです。
これで、条件 p と条件 q が同値（必要十分条件）ということが分かりました。
同値だと、
「実数 x が x－3 < 2 を満たす」ということを、
「実数 x が x < 5 を満たす」と書き換えることができます。
より複雑な計算であったとしても、同値な不等式で書き換えをするということを数学では、よく使います。
次に、「かつ」や「または」について説明をします。「かつ」は連立不等式の意味を表す論理なだけに、こちらから説明をします。
連立不等式 :「かつ」や「または」と不等式
実数 x が、
x < 6 …(1) かつ 4 < x …(2) を満たすというように、複数の不等式を同時に満たす範囲のことを連立不等式の解といいます。
実数 x が、(1) かつ (2) を満たすというと、(1) の不等式の範囲を満たし、(2) の不等式の範囲も満たしているということです。
「かつ」を使った不等式の記号の使い方ですが、
実数 x が、4 < x < 6 を満たすということが、(1) かつ (2) を満たすということを表します。
一般に、実数 a と b を定数とし、実数 a が、
不等式 a < x < b と表します。
これは、
a < x かつ x < b ということを意味しています。
不等式が表す範囲に「かつ」がつくと、それらの範囲をすべて満たすということになります。
「または」と以上・以下
一般に、p「または」q を満たすということは、次の三つの可能性を意味しています。
■ p を満たし q を満たさない
■ p を満たさないが q を満たす
■ p も q も両方とも満たす
二つの実数 a と b が与えられると、
a < b または a = b または a > b のいずれか一つのみを満たすということになります。
これを大学の数学で学習する実数の大小関係についての公理といいます。
「または」についての一般論では、23 = 8 通りの可能性があるわけですが、実数についての特別な大小関係についての性質ということで、「a < b, a = b, a > b のいずれか一つのみ」ということになります。
実数の大小関係を表す不等号なので、論理だけの一般論よりも言及された内容があるので、述べておきました。
「または」が絡むと、一般に分岐が複雑になりますが、「以上」と「以下」を表す不等号には、二つの可能性が示されているので、毎回、定義に基づいて判断をすることが大切になります。
x ≦ 3 というと、
「x < 3 または x = 3」ということを表しています。
「または」についての一般論で考えると、次の可能性があります。
■ x < 3 だが x = 3 でない
■ x < 3 でないが x = 3 である
■ x< 3 であり x = 3 でもある
ここで、実数の大小関係についての公理が効いてきます。
「x < 3, x = 3, x > 3 のいずれか一つのみ」が成立します。
この公理のもとで考えているので、
「x< 3 であり x = 3 でもある」という可能性が除外されます。
したがって、x ≦ 3 ということは、次の二つの可能性に絞られます。
■ x < 3 だが x = 3 でない
■ x < 3 でないが x = 3 である
この内容をまとめると、「x ≦ 3」ということは、
「x < 3」または「x = 3」であるということになります。
「x ≧ 3」についても、実数の大小関係についての公理が効いて、同様に、
「x > 3」または「x = 3」ということになります。
実は、不等式の両辺に同じ実数を加えても不等号の向きが変わらないということも実数についての大小関係の公理になります。
そのような公理を満たすという前提で、実数について議論することになります。
では、ここで、不等式についての命題が成立するかどうかを論理的に考える練習問題です。
連立不等式 :不等式についての命題も
【命題】
x を実数とする。
x が 4x－33 < x－15 を満たすことと、
x が x < 6 を満たすことは同値である。
＜証明＞
実数 x が、4x－33 < x－15 を満たしたとします。
不等式の性質から、両辺に 33 を加えても、不等号の向きは同じです。
そのため、x は、
4x < x+18 を満たすことになります。
さらに、両辺に 3x を加えると、
3x < 18 を実数 x は満たすことになります。
そして、両辺を 3 という正の実数で割っても、不等式の性質から、不等号の向きは同じです。
よって、実数 x は、
x < 6 を満たします。
これで、結論が導けました。
同値であることを示すために、逆についても示します。
実数 x が x < 6 を満たしたとします。
両辺に 3 という正の実数を掛けても、不等式の性質から、不等号の向きは同じです。
そのため、実数 x は、
3x < 18 を満たします。
さらに、両辺に x を加えると、
4x < x+18 を実数 x は満たすことになります。
そして、両辺から 33 を引くと、
実数 x は、
4x－33 < x－15 を満たすことになります。
これで、逆も示せたので、同値であることを示せました。 ■
一見すると、当たり前のことを正確に議論したのですが、こういった論理を正確に押さえることは、高校の数学を理解する上で大切になります。
例えば、数学２や数学Cで扱われる軌跡についてのアポロニウスの円に関して、逆の式の書き換えが成立するのかどうかということを確かめる際に、このような考察をすることになります。
今の命題は、一つの不等式の範囲についての書き換えでした。今度の練習問題は、連立不等式の問題です。
連立不等式の練習問題
【練習問題１】
実数 x が次の連立不等式を満たすとき、x の範囲を求めてください。
4x－33 < x－15 …(1)
4 < 2x …(2)
先ほど示した【命題】を使って、不等式を同値に書き換えます。
(1) を次の (3) に書き換えます。
x < 6 …(3)
このように、不等式を扱いやすい形に同値に書き換えることが大切になります。
(2) の不等式についても同値に書き換えます。
4 < 2x の両辺を 2 で割ると、
2 < x …(4) となります。
逆に、(4) を満たすと、両辺に 2 を掛けることで、
4 < 2x となります。
そのため、(2) と (4) は同値なので、
(2) を (4) に書き換えます。
すると、実数 x は、
x < 6 …(3) と、
2 < x …(4) を両方とも満たすことになります。
よって、実数 x は、
2 < x < 6 を満たすことになります。
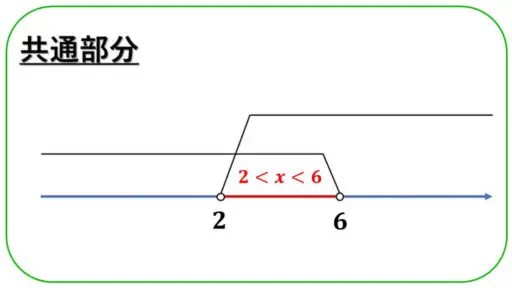
これで、【練習問題１】の答えとなる範囲が求まりました。
次の練習問題は場合分けが発生します。「かつ」と「または」を数学で定められている推論規則に基づいて議論を進めます。
連立不等式 :論理と場合分け
【論理の分配規則】
「pまたは(qかつr)」と「(pまたはq)かつ(pまたはr)」は書き換えることができる。
「pかつ(qまたはr)」と「(pかつq)または(pかつr)」は書き換えることができる。
この論理の規則は、「または」や「かつ」が分配できるということを意味しています。
a×(b+c) = a×b+a×c の要領で、「または」や「かつ」についての分配を行うことで、不等式を扱いやすい形に書き換えることも大切です。
「×」を「または」（もしくは「かつ」）と考えて、分配します。
この分配は、「または」と「かつ」が三つの条件において混じっているときに有効です。
※ 分配律という記事で、二項演算において n 個で成立するという一般の分配法則を帰納法を用いて証明をしています。
三つの条件について、すべて「または」のときや、すべて「かつ」のときは、論理の規則で結合律が認められているので、括弧のつけ方を替えることができます。
※ 結合律という記事で、二項演算についての一般の結合律を証明しています。大学の代数学の入門的な内容で扱われる基礎となる命題になります。
【論理の結合律】
「pまたは(qまたはr)」は「(pまたはq)またはr」と書き換えることができる。
「pかつ(qかつr)」は「(pかつq)かつr」と書き換えることができる。
この論理の結合律を、二項演算と同じように、使いこなせると、不等式の考察に強くなります。
では、場合分けが発生する連立不等式を、論理の規則に基づいて考察します。
場合分けをする連立不等式問題
【練習問題２】
実数 x が、次の連立不等式を満たすとき、x の範囲を求めてください。
4x－33 < x－15 …(1)
|x－2| > 3 …(2)
先ほどと同じように【命題】を使って、(1) を同値な次の (3) に書き換えます。
x < 6 …(3) を実数 x が満たすということと同値でした。
(2) は、絶対値の定義から、次の (4) と同値になります。
x－2 > 3 または －(x－2) > 3 …(4)
－(x－2) > 3 は、両辺に －1 を掛けることで、
(x－2) < －3 と同値です。
負の実数を両辺に掛けると、不等号の向きが逆になるというのも不等式の性質（実数の大小関係についての公理）になります。
そのため、(4) は (5) と同値になります。
x－2 > 3 または x－2 < －3 …(5)
これらの内容から、「実数 x が (1) かつ (2) を満たす」ということと、「実数 x が (3) かつ (5) を満たす」ということが同値になります。
さらに、同値なものを書き換えます。
(3) かつ (5) をさらに詳しく見てみます。
「x < 6 かつ（x－2 > 3 または x－2 < －3）」となっています。
三つの条件において、「または」と「かつ」が混ざっています。こういったときに、論理の分配規則を使って書き換えるチャンスです。
「x < 6 かつ x－2 > 3」または「x < 6 かつ x－2 < －3」…(6) と同値になります。
ゆえに、「実数 x が (1) かつ (2) を満たす」ということが、「実数 x が (6) を満たす」ということが同値に書き換えることができます。
さらに、(6) を不等式の性質に基づいて、書き換えます。
「x < 6 かつ x－2 > 3」は、
「x < 6 かつ x > 5」と同値です。
これは、不等号の表し方から、
「5 < x < 6」のことです。
ゆえに、(6) は、
「5 < x < 6 または (x < 6 かつ x－2 < －3)」…(7) と同値です。
x < 6 かつ x－2 < －3 も、不等式の性質を使って、書き換えます。
x < 6 かつ x < －1 と同値です。
これは、実数 x が x < －1 を満たすことと同値になります。
実数 x が 「x < 6 かつ x < －1」 を満たせば、実数 x が「x < －1」を満たします。
逆に、実数 x が「x < －1」を満たせば、実数 x が 「x < 6 かつ x < －1」 を満たします。
これで、(x < 6 かつ x－2 < －3) の部分を、
x < －1 に書き換えることができます。
よって、実数 x が (7) を満たすことは、
実数 x が、
「5 < x < 6 または x < －1」を満たすことが同値ということが分かりました。
以上をまとめると、
実数 x が (1) かつ (2) を満たすことと、
実数 x が 5 < x < 6 または x < －1 を満たすことが同値です。
これが、答えとなる x の範囲です。
連立不等式と場合分けが絡むと、「かつ」や「または」についての論理規則を使って、不等式を扱いやすい形に書き換えることが重要になるときがあります。
この記事では、論理を中心に書き換えを考えました。もちろん、計算による不等式の同値な書き換えも大切ですし、数直線やグラフを用いて、図形的に考察することが効くときもあります。
今の練習問題だと、
y = 3x－18 という一次関数の y の値が 0 未満となる x の範囲と、y = |x－2| という絶対値つきの関数の y の値が 3 より大きくなる x の範囲の共通部分が求める x の範囲となります。
※ 絶対値という記事で、絶対値の定義と関数の対応について、解説をしています。
論理と集合、計算による変形、図形的な情報を工夫して、高校の数学の不等式問題を考えるということになります。
連立不等式から、さらに必要や十分条件についての考察を使う二次方程式の解の存在範囲の問題があります。
中には記述答案に書かない条件も判断することがあります。
そういったときにも、やはり論理の規則が大切になります。
それでは、これで論理を中心に扱った今回の記事を終了します。
読んで頂き、ありがとうございました。