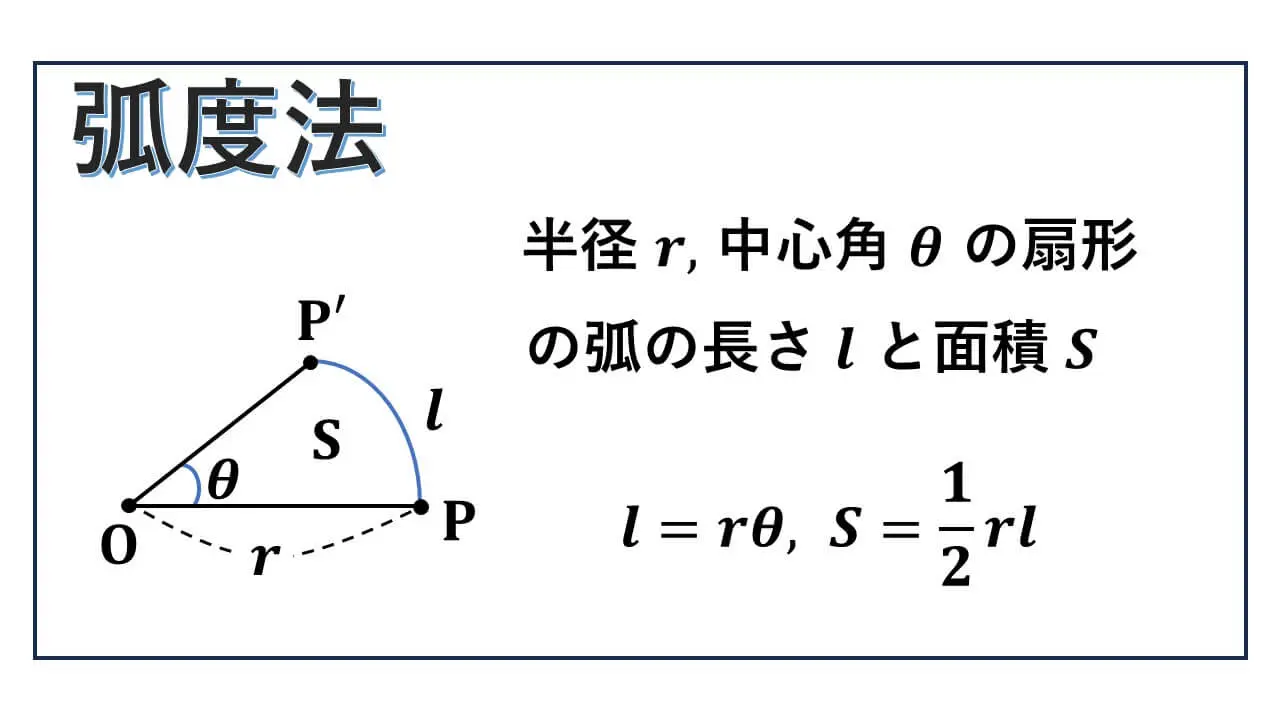
弧度法 ラジアン | 弧の長さが半径に等しいときを基準に中心角を決定する
" 弧度法 “で中心角の大きさを測るとき、弧の長さが半径に等しいときを基準にして、比例関係を使って角の大きさを求めます。
円の半径は、円によって様々ですが、「弧の長さが半径に等しくなったとき」をもとにして、比例の計算で中心角の大きさを決めます。
まさに算数や中学の数学で学習した単位当たりの量の考え方が、下支えになる数学IIの弧度法です。
1 ラジアン (radian) の定義の把握に、弧の長さが中心的な役割を果たします。
図を使いつつ、定義を押さえることで、公式を自分で導くことが大切になる単元内容になります。
この記事では、数学IIIでも使う「弧の長さと半径と中心角についての公式」や、「扇形の面積の公式」を導くことを主眼に解説をしています。
弧度法 :弧の長さから比例で
始線の上にある点 P が左回りに動いて点 P’ の位置まで来たときに、形成された扇形OPP’ の中心角は正の大きさの角度です。
（点 P が右回りに動いて、できた角の大きさは負の角度になります。）
左回りと右回りの違いは、角の大きさにマイナス「－」をつけて調整すれば良いので、この記事では正の大きさの角度に焦点を当てて解説をします。
大切になるのが、「弧の長さ」から 1 ラジアンという中心角の大きさを、どのように定義されているのかを押さえることになります。
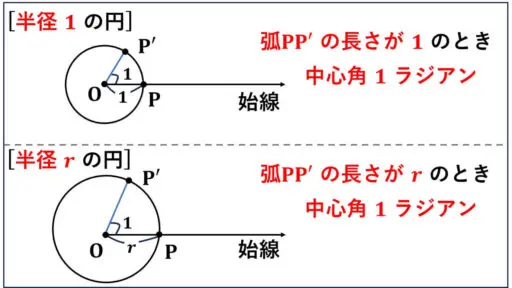
まず、円の半径が 1 という特殊な場合から説明します。
動く半径である動径 OP’ が、弧OP’ の長さが半径と同じ長さになったときに注目します。
弧OP’ の長さが半径と同じになったときに形成された扇形OPP’ の中心角の大きさを 1 ラジアンと定義します。
円の半径が 1 なので、
「弧の長さ 1 : 中心角 1 ラジアン」という関係になります。
弧の長さから、比例を用いて、中心角を計算します。
さらに OP’ が動いて、弧の長さが 2 となったとします。
このときに、中心角の大きさを x ラジアンとします。
比例の関係によって、
「弧の長さ 1 : 中心角 1 ラジアン」という関係から x の値を決めます。
1 : 1 = 2 : x として、
外項の積と内項の積が等しいということから、x の値を決定することになります。
そのため、
1 × x = 1 × 2 という等式を作ります。
すなわち、
x = 2 （ラジアン）と決まりました。
「弧の長さ 1 : 中心角 1 ラジアン」という関係をもとにして、弧の長さから中心角の大きさを確定させるということが基本となります。
弧の長さが 3 のときの中心角の大きさ y ラジアンだと、同じ様に比例の計算をもって定めます。
1 : 1 = 3 : y より
y = 3 となります。
動いた点 P’ の位置から弧PP’ の長さが与えられると、
中心角 ∠POP’ の大きさが
比例の関係から自動的に決定します。
今、半径 1 という特殊な円で考えていると、弧の長さがストレートに中心角の大きさとなっていました。
一般の半径 r の円で、どうなるのかまで押さえるためには、根本となる仕組みを押さえることが大切になります。
その仕組みが、やはり弧の長さから中心角の大きさを決めるということになります。
半径rの場合
【定義】
弧PP’ の長さが半径の長さ r に等しくなったとき、扇形OPP’ の中心角の大きさを 1 ラジアンと定義する。
この定義から出発して、比例の関係を使って、中心角の大きさを定義します。
「弧の長さ r : 中心角 1 ラジアン」という関係をもとにして、弧の長さから中心角の大きさを定めます。
半径 r の円において、定義から大元の比例の関係が「弧の長さ r と 1 ラジアン」という比率になります。
例えば、
弧PP’ の長さが 7 のとき、
∠POP’ の大きさを z ラジアンを定める比例の計算を考えます。
r : 1 = 7 : z より
r × z = 1 × 7 となります。
両辺を r で割ると、
z = 7 ÷ r となります。
これで定数である半径の長さ r を使って、中心角の大きさ z ラジアンを表すことができました。
弧の長さが半径の長さ r と等しくなったときに注目し、
「弧の長さ r : 中心角 1 ラジアン」という関係をもとにして比例の計算をすることで、中心角の大きさが決まります。
これで、一般の半径 r の扇形について、弧の長さから中心角の大きさを定義することができました。
ここで、度数を用いた角の大きさとラジアンについての関係も押さえたいところです。
30°といった度数法による角の大きさと、ラジアンを単位とする弧度法による角の大きさを自由に変換できるようにするために、円周率 π を利用します。
弧度法 :ラジアンと度数の変換
半径 r の円では、半円の弧の長さは、
(2 × r × π) ÷ 2 より、
πr となっています。
半円の中心角の大きさは 180°です。
弧の長さが πr なので、弧度法で 180°の大きさの中心角を表すことができます。
180°の大きさに対応する角の大きさを x ラジアンとして、比例の関係から x の値を定数を用いて表します。
「弧の長さ r : 中心角 1 ラジアン」という関係から、
r : 1 = πr : x です。
よって、rx = πr です。
半径 r > 0 より、両辺を r で割ると、
x = π （ラジアン）です。
これで度数法の 180°に対応するのが π ラジアン (rad) ということが分かりました。
度数法で、弧の長さは中心角の大きさに比例していて、弧度法で中心角の大きさは弧の長さに比例していました。
そこで、比例の関係から、1° に対応するのが何ラジアンかを計算することができます。
「180° : π rad」という関係なので、単位を外して実数の値にだけ注目します。
1°に対応するのが y ラジアンとして、比例の計算をします。
180 : π = 1 : y より
180y = π だから、
y = π ÷ 180 （rad）です。
これで、1° と (π ÷ 180) ラジアンが対応することが分かりました。
三角関数を考えるときに、角の大きさをラジアンで表し、単位は省略して実数の値だけを定義域の要素とします。
このときに、度数をラジアンに変換するのですが、求めた度数とラジアンの対応から、比例を使って計算できます。
度数をラジアンに変換する例
1 : (π ÷ 180) の関係から比例の計算をします。
30°をラジアンに変換するときだと、
対応するのが x ラジアンだとして、
1 : (π ÷ 180) = 30 : x から
x = 30 × (π ÷ 180) となります。
約分をすると、
x = π/6 と三角関数で、よく使う有名角についてのラジアンの形になります。
この要領で、90°に対応するのが x ラジアンだとすると、
x = 90 × (π ÷ 180)
= π/2 となります。
比例の関係を押さえておくと、自分で計算で値を求めることができるので役に立ちます。
ここまで弧の長さから中心角をラジアンで表す弧度法について述べてきました。
ここからは、基礎となる定義の内容を公式の形にまとめ、扇形の面積を表す公式を導くことを考えます。
弧度法 :扇形の面積の公式
半径 r の扇形について、弧の長さが半径 r と等しくなったときに、
「弧の長さ r : 中心角 1 ラジアン」という関係をもとにして、比例の関係で中心角の大きさをラジアンで表しました。
この関係から、比例の計算で、弧の長さが l のときに、中心角 θ ラジアンとの関係式を求めます。
r : 1 = l : θ より、
l = rθ という等式が得られます。
半径 r を定数として固定しておくと、弧の長さ l が 2 倍 3 倍となると中心角 θ も 2 倍 3 倍となる、つまり、「中心角の大きさが弧の長さに比例する」ということになります。
円周角の大きさは中心角の半分の大きさなので、「円周角の大きさも弧の長さに比例する」ということになります。
公式として、まとめておきます。
【公式１】
半径 r の扇形の弧の長さが l で、中心角が θ ラジアンであるとき、
l = rθ が成立する。
ここで、単位を省略している r, l, θ は、すべて実数となっていることにも注意です。
θ ラジアン ですが、扇形や円を考えているときに、動径が円の周上を一周すると、もとの始線の上にあった点 P の位置に戻ってきます。
そのため、360°に対応する 2π ラジアンの分だけズレても、同じ大きさの角を表すことになります。
そのため、n を整数として、
θ + 2πn や θ － 2πn は、
どちらも角の大きさは θ と等しいと考えます。
つまり、
角の大きさについて、
θ = θ ± 2πn ということになります。
では、もう一つの重要な公式である扇形の面積の公式を導きます。
先ほど導いた【公式１】から、弧の長さと扇形の面積が結びつきます。
変数と定数の観点から
半径 r の扇形が与えられたとき、中心を同じとする半径 r の円を考えます。
その円の面積は、πr2 です。
中心角の大きさに依存せずに、与えられた扇形の半径 r という定数と円周率 π という定数だけで円の面積が表されています。
ここで、円形のピザを中心角で等分したうちの一つという見方をします。
円の 360°のうちに、中心角 θ ラジアンが占める割合を考えます。
360°をラジアンに変換すると、2π ラジアンです。
2π ラジアンのうち、θ ラジアンの占める割合から扇形の面積を求めます。
ここで、扇形の中心角を θ という変数として、半径 r で中心角 θ ラジアンの扇形の面積 S を求めます。
中心を同じにする半径 r の円の面積 2π の中で、扇形の面積 S が占める割合を表す数字を計算します。
θ ÷ 2π が割合を表す実数となっています。
「円の面積 × 割合を表す数」が、「扇形の面積 S」となります。
S = πr2 × (θ ÷ 2π)
= 1/2 × r2θ となります。
これで、【公式２】として、扇形の面積を表す式が得られました。
ここで、扇形の弧の長さを l とすると、
【公式１】から、l = rθ でした。
面積の公式から、中心角 θ を消去して、弧の長さから一気に面積までジャンプした等式が得られます。
S = 1/2 × r × rθ
= 1/2 × r × l となります。
これで、三つ目の【公式３】が得られました。
ここまでの扇形についての公式をまとめます。
扇形や円は、高校一年の三角比の段階から、三角関数への土台として関わってきます。
このような三角比の内容を基礎として、三角関数の内容へと発展し、角の大きさの単位としてラジアンが使われます。
【関連する記事】
■ 正弦定理（三角比）
■ 三平方の定理（余弦定理へ拡張）
■ 和積変換公式（数II）
このような基礎となるラジアンという単位で角の大きさを測る弧度法について、この記事では弧の長さを用いた定義から扇形の面積の公式までの議論を解説しました。
この扇形の弧の長さについて導いた公式ですが、数学IIIの極限の単元でも重要な公式の導出に役立ちます。
はさみうちの定理という記事で、sin や cos についての極限に関する公式を解説しています。
大学の解析学の理論の証明は厳密ですが、その内容を高校の数学から少し見るということができるときもあります。
球の表面積という記事で、弧の長さに注目して微小な長方形を使って、曲面の面積に関わる内容に触れています。
厳密な証明はせずに、数学IIIの計算に留めることにして、曲面の面積についてのイメージについて気軽に述べています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。