無限次元ベクトル空間-例-実数列 | 抽象ベクトルに親しむ大学の内容【線形代数学】
" 無限次元ベクトル空間 – 例 – 実数列 “について、抽象的なベクトルについて解説をしています。
線形代数の公理を満たす集合の元を（抽象的な）ベクトルといいます。
高校の数学で学習した矢印でないものも抽象的なベクトルとなっているので、戸惑うかもしれませんが、公理を満たせばベクトルということに慣れないと先へ進みにくくなってしまいます。
はじめて水泳を学習するときに、いきなり千メートルを泳ぐということをせずに、まずは水に顔をつけるくらいのことから始めます。
大学の数学科の線形代数学や微分積分学を理解しようとするときに、高校の数学から、ゆっくりと歩き出すと、自然と親しめるかと思います。
大学受験の頻出内容で、数列について係数比較をして未知数を決定するという内容が出てきます。
しかし、その背景を理解するには、大学で扱う抽象的なベクトル空間についての理論が関わります。
そこで、抽象的なベクトルの一次独立に関わる内容を取り挙げています。
この記事では、自然数全体を N、実数全体を R として議論を進めます。
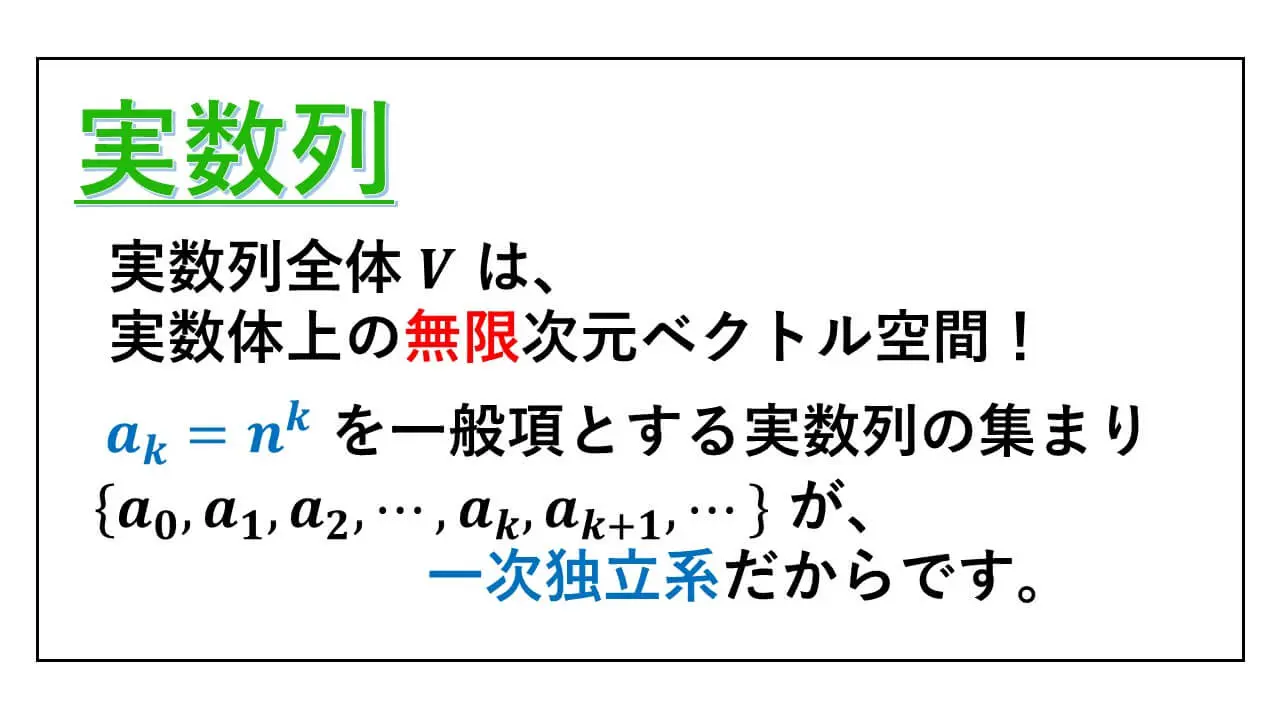
無限次元ベクトル空間 – 例 – 実数列
各自然数 n に対して、第 n 項の実数値 an が定められているとき、実数列 {an} が与えられていると高校の数学で学習します。
どの自然数 n についても、第 n 項の値が定められているということが大切になります。
さらに、実数列 {an}, {bn} が与えられたとき、二つの数列が等しいかどうかという相当関係を押さえておく必要があります。
等しいか等しくないかという基本を押さえることで、大学数学への理解が進みます。
「各自然数 n について、第 n 項に配置されている実数値 an と bn が同じ実数となっている」とき、数列 {an} と数列 {bn} が等しい実数列と定義されています。
ここまでの内容ですが、写像（関数）の対応の考え方で表すことができます。
各自然数 n に対して、第 n 項の実数値 an が定められているということは、自然数全体から成る集合 N に対して、an という実数を対応させているということになります。
実数全体を R とし、N → R という N を定義域とする写像（関数）が与えられたということになります。
そうすると、N を定義域とし、R の値を対応させるという写像 f, g についての写像の相等関係の定義が考えられます。
定義域 N のどの元 n についても、
f(n) = g(n) となっているとき、f と g が等しい写像であるというのが写像の相等関係です。
等しいときに、f = g と表します。
これが、先ほど述べた実数列 {an} と {bn} が等しいことの定義と照らし合わせてみます。
「各自然数 n について、第 n 項に配置されている実数値 an と bn が同じ実数となっている」とき、数列 {an} と数列 {bn} が等しい実数列ということでした。
これは、N から R への写像としての相等関係の内容となっています。
ここまでの内容を踏まえた上で、写像の対応の記号を使って、数列を表すことにします。
そうすると、抽象的なベクトルが見えてきます。
写像の記号で表す
各自然数 n に対して、第 n 項の実数値 an が定められているとき、実数列 {an} が与えられているという高校数学で見慣れた記号を、写像の記号で表します。
f : N → R で、
各 n∈N に対して f(n)∈R が定義されているということになります。
∈ は集合に含まれる元（要素）ということを表す記号になります。
この数列の記号を写像で表すという一歩を踏み出すことが最初のハードルです。
高校の数学IIIで、「数列の収束」と「関数の収束」という単元の区切りがあります。
ここで、表面的な言葉遊びで、数列は関数でないと早とちりをしてしまうと、実数列全体が R 上のベクトル空間（線形代数）となっていることが分からなくなってしまいます。
自然数全体 N が離散的であるのに対して、実数全体 R がつながっている（稠密である）ということで極限の定義が違っています。
イプシロンエヌ法とイプシロンデルタ論法という二つを大学の微分積分学で学習します。
この違いに関わってくる内容となります。
しかし、この内容と関係なく、関数（写像）の一対一対応ということが数学では考えられています。
有理数の稠密性の議論の前段階で、写像（関数）の対応は考えられていますので、安心して数列を写像（関数）として考えることに慣れるのが大切になります。
定義域である N の各元 n について、f(n) という実数が定義されているということが押さえるポイントになります。
これを高校の数学の数列の言葉で表すと、各自然数 n に対して、第 n 項に配置されている実数値が f(n) ということです。
では、実数列全体から成る集合 V が、R 上のベクトル空間となっているということを確認します。
そのためには、実数列どうしの加法と、R から実数列へのスカラー倍を定義するところから始めます。
無限次元ベクトル空間 – 実数列 :公理の確認
【実数列どうしの加法】
f, g を N から R への写像（実数列）とする。
このとき、
各 n∈N に対して、
f+g という N から R への一対一対応を次で定義する。
各 n∈N に対し、
(f+g)(n) を 実数 f(n) と 実数 g(n) の R における加法で定義する。
すなわち、
(f+g)(n) = f(n)+g(n) と定義する。
すると、この f+g は、N から R への写像となっている。
ここで、和を表している記号について補足しておきます。
各自然数 n について、
f(n)+g(n) は、実数 f(n) と実数 g(n) で、高校のときから計算をしている実数の加法を計算した値を表しています。
それに対して、f+g は、写像 f と写像 g の加法を表しています。
これも N から R への写像なので、
f+g : N → R ということです。
この実数列という写像についての加法の定義について、ベクトル空間の公理を満たすかを確認することになります。
正確には、さらに R から実数列へのスカラー倍を定義した上で、公理を確認することになります。
【R からのスカラー倍】
実数列 f : N → R と、r∈R が与えられたとき、rf という実数列を次のように定義する。
各 n∈N に対して、
(rf)(n) を実数 r と 実数 f(n) の乗法を計算した値と定義する。
すなわち、
(rf)(n) = rf(n) と定義する。
そして、この rf という実数列を、実数 r によって実数列 f をスカラー倍してできた実数列という。
rf(n) も実数なので、
rf(n)∈R です。
それゆえに、
rf : N → R となっています。
これで、実数列全体を V と表すと、
V×V → V という二項演算である加法と、
R×V → V という R から V へのスカラー倍が定義されました。
ここから、ベクトル空間の公理を確認します。
条件がたくさんあって、手間どりますが、全て確認します。
実数列の加法は結合的で交換的
実数全体 R における加法の結合法則と交換法則を頼りに、実数列どうしの加法について結合法則と交換法則が成立することを確かめます。
ここで、上で述べた二つの写像の相等関係の定義が関わってきます。
【加法の結合法則の確認】
f, g, h∈V について、
(f+g)+h と f+(g+h) が等しいということを示すことになります。
そこで、N → R という写像の相等関係を確認することになります。
各 n∈N について、
((f+g)+h)(n)
= (f+g)(n)+h(n)
= (f(n)+g(n))+h(n) …(1)
実数列の加法の定義に基づいて計算をしました。
大学の数学では、中括弧を使わなくて良いことにも注意です。
また、
(f+(g+h))(n)
= f(n)+(g+h)(n)
= f(n)+(g(n)+h(n)) …(2)
ここで、実数全体 R における加法の結合法則を使います。
(f(n)+g(n))+h(n)
= f(n)+(g(n)+h(n)) …(3)
(1), (2), (3) より、
((f+g)+h)(n) = (f+(g+h))(n)
よって、写像の相等関係の定義から、
(f+g)+h = f+(g+h) となっていることが確認できました。
数列の言葉では、
各自然数 n に対して、
実数列 (f+g)+h と f+(g+h) の第 n 項の値として、同じ実数が配置されていることが確認できました。
【加法の交換法則の確認】
f, g∈V に対して、
f+g = g+f を示します。
各 n∈N に対して、
R における加法の交換法則より
f(n)+g(n) = g(n)+f(n) となっています。
そのため、
(f+g)(n)
= f(n)+g(n)
= g(n)+f(n)
= (g+f)(n)
すなわち、f+g = g+f です。
まだ確認すべきベクトル空間の条件が残っています。
ここで、零とは何かということを意識する必要が出てきます。
実数列 :零写像が加法零元
実数全体 R における加法零元は、実数の 0 です。
しかし、実数列全体 V の加法零元は、実数の 0 ではありません。
次に定義する零写像という定数値関数が V の加法零元となります。
【零写像】
各 n∈N に対して、
z(n) = 0 ∈R と定義する。
z : N → R である。
どの自然数 n に対しても、実数の 0 を対応させるという写像を z と定めました。
確かに、z は N を定義域として、実数を対応させているので、実数値関数です。
そのため、z ∈V となっています。
この特別な写像 z が、V の加法零元となっていることを確認します。
つまり、各 f∈V に対して、
f+z = f ということを示します。
各 n∈N に対して、
(f+z)(n) = f(n)+z(n)
= f(n)+0 = f(n) です。
写像の相等関係より、
f+z = f となっています。
次に加法逆元の存在を示します。
ここで、実数からのスカラー倍が効果を発揮します。
f∈V に対して、－1 という実数からのスカラー倍を－f と表すことにします。
－f : N → R は、
各 n∈N に対して、
(－f)(n) = －1 × f(n) のことです。
－1 × f(n) は、実数 f(n) の符号を逆転させた－f(n) のことです。
やはり、各自然数に対して、
実数を対応させているので、
－f ∈V です。
－f が、f の加法逆元となっていることを確認します。
各自然数の動きを追う
各 n ∈N に対して、
(f+(－f))(n)
= f(n)+(－f)(n)
= f(n)+(－f(n))
= 0 = z(n)
写像の相等関係から、
f+(－f) = z となっています。
z が V の零元だったので、
－f は f の加法逆元となっています。
ここで、スカラー倍についての条件を確認しておきます。
1 ∈R という実数においての乗法単位元からのスカラー倍を考えます。
f ∈ V について、
各 n∈N に対し、
(1f)(n) = 1 × f(n) = f(n) です。
そのため、1f = f です。
1 で V の元をスカラー倍しても、同じ実数列のままとなっています。
さらに、r, s∈R と f ∈V について、
各 n∈N に対して、
((rs)f)(n) = (rs) × f(n)
= r × (s × f(n))
= r × (sf)(n)
= (r(sf))(n) です。
写像の相等関係から、
(rs)f = r(sf) となっています。
これは、実数の乗法についての結合法則が決め手になりました。
さらに、実数の乗法についての交換法則も考慮すると、次の相等関係が得られます。
r(sf) = (rs)f = (sr)f = s(rf) となっています。
後は、加法とスカラー倍の関係を示す条件についての確認だけが残っています。
実数についての分配法則が決め手になります。
加法とスカラー倍をつなぐ
f, g∈V, r∈R について、
各 n∈N に対して、
(r(f+g))(n)
= r × (f+g)(n)
= r × (f(n)+g(n))
= r × f(n)+r × g(n)
= (rf)(n)+(rg)(n)
= (rf+rg)(n) です。
写像の相等関係から、
r(f+g) = rf+rg となっています。
後、一つです。
r, s∈R と f ∈V について、
各 n∈N に対して、
((r+s)f)(n)
= (r+s) × f(n)
= r × f(n)+s × f(n)
= (rf)(n)+(sf)(n)
= (rf+sf)(n) です。
写像の相等関係から、
(r+s)f = rf+sf となっています。
これで、実数列全体 V が R 上のベクトル空間（線形代数）となっていることの確認が完了しました。
高校の数列では、初項 2、交差 3 の等差数列 {an} の第 n 項の値を一般項といいました。
an = 2+3×(n－1) = 3n－1 と表していました。
この記事で述べた写像の記号を使うと、
各 n∈N について、
f(n) = 3n－1 と写像を定め、
f : N → R だから f ∈V ということになります。
f(n) = 3n－1 といった形は、関数（写像）については、多項式関数といわれます。
この多項式関数について、無限個の元から成る一次独立系の存在について説明をします。
そのため、先ほどの実数列全体 V が、R 上の無限次元ベクトル空間となっていることが理解できます。
実数列 :無限次元の例
数列ということで、定義域を N としていました。
高校一年から使っている定義域が R となっている関数も考えることにします。
R から R への関数全体を W とすると、先ほどと同様の議論で W も R 上のベクトル空間となっていることが分かります。
各 0 以上の整数 n に対して、
fn : R → R を、
x ∈R に対して、
fn(x) = xn と定義します。
特に、整数 0 に対しては、
f0(x) = x0 = 1 という定数関数となっています。
n = 1 のときは、fn は 一次関数、
n = 2 のときは、fn は二次関数で高校の頃から使っている関数です。
※ f2 などは線形写像ではないので注意です。
高校の数学IIIで学習したように、各 fn は微分可能です。
それぞれの 1次導関数を fn と表すことにします。
ここで、
{f0, f1, … } という無限個の関数からなる W の部分集合を考えます。
実は、{f0, f1, … } は一次独立系となっています。
同じ記号ですが、零写像を z と表しておきます。
つまり、z : R → R は、
各 x ∈R に対し、z(x) = 0 です。
抽象的な一次独立
n を 0 以上の整数とする。
このとき、{f0, f1, … } は W の一次独立系である。
＜証明＞
n = 0 の場合から考えます。
r∈R について、rf0 = z とします。
零写像 z の定義から、
r = r×10 = (rf0)(1) = z(1) = 0 です。
ゆえに、{f0} は 一次独立系となっています。
次に n ≧ 1 のときに、
n = k について
{f0, f1, … , fk} が一次独立系なら
{f0, f1, … fk, fk+1} も一次独立系であることを示します。
ここで、
fk+1 が、{f0, f1, … , fk} の一次結合で表せたと仮定します。
つまり、
{f0, f1, … fk, fk+1} が一次従属系だと仮定したわけです。
すると、
ある実数 r0, … , rk が存在し、
fk+1 = r0f0+r1f1+…+rkfk と表すことができます。
等しい関数なので、1次導関数も等しくなっています。
そのため、
fk+1 = r0f0+r1f1+…+rkfk となっています。
x ∈R を定義域に含まれる任意の元とします。
0 ≦ i ≦ k+1 について、
rifi (x) = ri(i－1)xi－1 となっています。
i = 0 については、実数の 0 となって和から消えています。
1次導関数によって、x を移した値は次のようになります。
今、{f0, f1, … , fk} が一次独立という前提で議論をしていました。
これは矛盾です。
そのため、背理法から、
{f0, f1, … fk, fk+1} が一次独立系となります。
以上より、数学的帰納法から、
0 以上の整数 n について、
{f0, f1, … , fn} が一次独立ということを示すことができました。
線形代数学の一般論ですが、有限個の一次独立系から、有限個の元から成る空でない部分集合を選んだとき、その有限集合は一次独立系になります。
そのため、
{f0, f1, … } は W における無限個の元から成る一次独立系となっています。【証明完了】
一般に、有限次元ベクトル空間 U において、U における一次独立系を形成するベクトルの個数は、U の次元以下となります。
つまり、dim U が一次独立系を形成するベクトルの最大個数となるわけです。
今、示したことから、W には無限個の元から成る一次独立系が存在しました。
そのため、W の次元は有限ではありません。
つまり、W は無限次元のベクトル空間となっています。
ここで、{f0, f1, … } の各元 fi について、定義域を N に制限した関数を *fi と表すことにします。
*fi : N → R ですから、実数列です。
そのため、
{*f0, *f1, … } ⊂ V となっています。
同様の議論をすると、
{*f0, *f1, … } は V における無限個の元から成る一次独立系です。
そのため、実数列全体から成るベクトル空間 V は無限次元でなければなりません。
実数値の多項式関数全体を生成する基底の存在証明になる内容を述べました。
この一次独立ということが、高校の数学で使っていた数列についての係数比較の背景です。
係数比較と一次独立
数列 {an} と数列 {bn} が自然数全体において恒等的に等しいとします。
an = 3n2+2n+5,
bn = pn2+2n+5 をそれぞれの一般項とします。
このとき、実数 p の値を求めてください。
高校の数学では、恒等式の内容で、係数比較をしました。
二次の項について係数が等しいため、
p = 3 と値を決定したわけです。
この内容を多項式関数の一次独立系の内容で再考してみます。
数列 {an} と数列 {bn} が自然数全体において恒等的に等しいということは、各自然数 n について、第 n 項の値が等しくなっているということでした。
そして、{*f2, *f1, *f0} が一次独立系です。
数列 {an} を一次結合で表すと、
3*f2+2*f1+5*f0 です。
各自然数 n について、
第 n 項の値は、
3n2+2n+5 となっているわけです。
数列 {bn} を一次結合で表すと、
p*f2+2*f1+5*f0 です。
各自然数 n について、第 n 項の値が等しいということは、関数（写像）が等しいということでした。
そのため、
3*f2+2*f1+5*f0
= p*f2+2*f1+5*f0 です。
ここで、ベクトル空間 V における計算をします。
(p－3)*f2+(2－2)*f1+(5－5)*f0 = z です。
z は零写像で、V の加法零元でした。
一次独立だから、
p－3 = 2－2 = 5－5 = 0 です。
この p－3 = 0 の部分だけを取り出して、係数比較と高校の数学では言っていたということです。
これが、p = 3 という係数比較についての背後にある線形代数学の理論です。
関連する記事として、有限次元における線形写像についての記事も投稿しています。
退化次数という記事では、今回と違って、有限次元のベクトル空間についての内容となっています。
また、環論を見据え、
End(V)という線形変換の成す環についての記事も投稿しています。
大学の数学を学習するときに、写像についての基礎的な内容をよく使います。
全単射という記事で、集合論の入門的な内容を解説しています。
始集合と終集合に関連した内容については、写像による像と原像という記事を投稿しています。
これで、今回のタロウ岩井の記事を終了します。
読んで頂き、ありがとうございました。