群の公理 | 定義から各元についての逆元が、ただ一つであることなどを導く
" 群の公理 “から、数学で認められている論理の規則に基づき、基礎的な命題たちを導いています。
その一つの命題として、「群 G の各元についての逆元は、ただ一つである」という命題があります。
認められている公理系から、数学的推論をもって、命題たちを導くということについて、途中の過程を省略せずに、じっくりと解説をしています。
二項演算が定義されている空集合ではない集合 G が、群の公理である三つの条件を満たしているというところから議論を進め、基礎的な命題を導きます。
f : G × G → G が G における演算ですが、
任意の (g, h)∈G × G に対し、
f(g, h) のことを単に gh と表すことにします。
それでは、基礎的な命題を証明します。
群の公理 :単位元は唯一
【群の公理】
二項演算をもつ空集合ではない G が、次の三つの条件を満たすとき、G を群という。
[1] 結合律を満たす
[2] 左かつ右単位元 e が存在する
[3] G の各元には左かつ右逆元が存在する
[1] の結合律については、三つの元で成立すると、一般に n 個の元について括弧のつけ方に依らずに演算の値が一つに確定するということをリンク先の記事で証明しています。
[2] の単位元 e∈G は、正確には左単位元であり、かつ、右単位元ということです。
つまり、∀g∈G に対し、
eg = g, ge = g ということです。
この単位元 e ですが、群 G の単位元(左かつ右単位元)は、唯一であることを証明します。
証明の前に、[3] の逆元について説明しておきます。
g∈G に対して、
x∈G が xg = gx = e を満たすとき、x を g の左かつ右逆元といいます。
左逆元であり右逆元でもあるということを群の公理の条件の一つとしています。
この左かつ右逆元の存在も唯一になります。
これも公理から、すぐに導ける命題なので、後で証明をします。
それでは、G の単位元は、e の他には存在しないということを証明します。
条件を満たすと必ずe
h∈G が、任意の g∈G に対し、
hg = gh = g を満たしたとします。
この h が、e に一致しているということを示すと、G において左かつ右単位元となっている G の元が e しかないということになります。
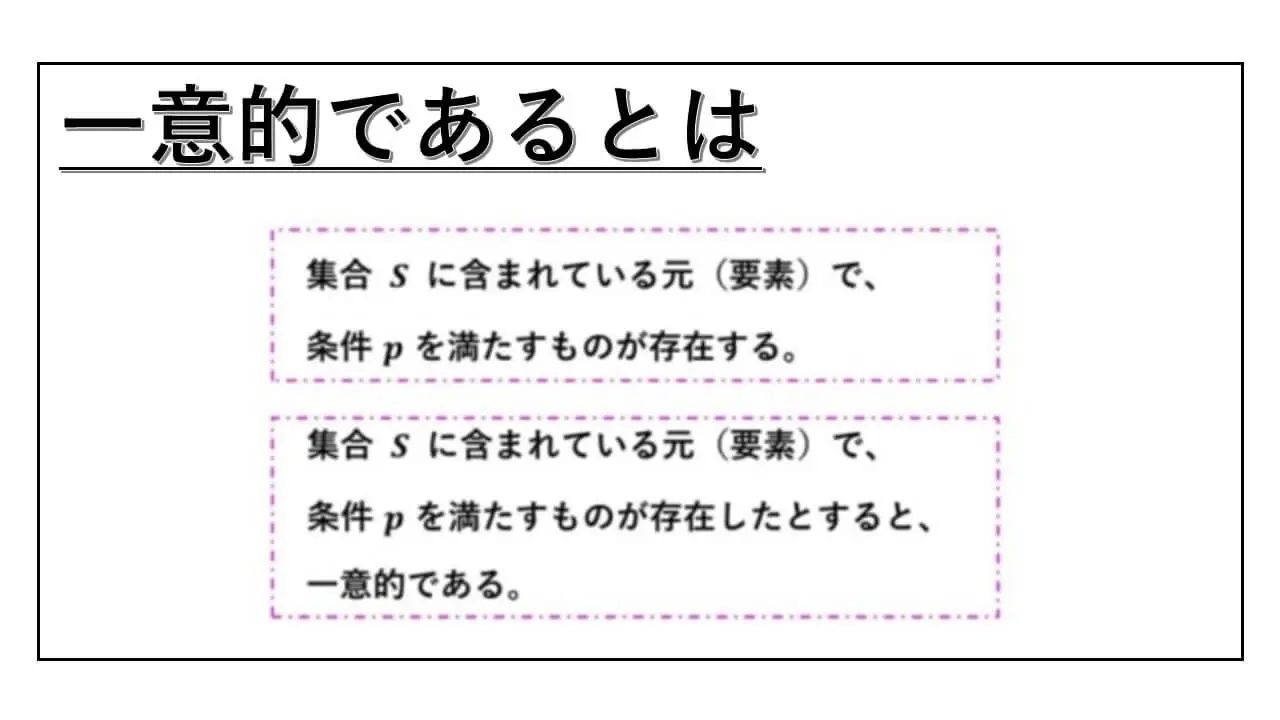
※ 一意という記事で、典型的な唯一性の証明について解説をしています。
g として、特に e∈G を考えます。
h は任意の G の元に対して、左かつ右単位元の条件を満たしているので、e について、次のようになります。
そのため、he = e です。
ここで、e は単位元なので、h の右単位元になっています。
よって、he = h です。
すなわち、
h = he = e となっています。
これは、h = e ということです。
これで、任意の G の元に対して、左かつ右単位元であるという条件を満たす G の元は、e に限るということを示すことができました。
次に、逆元の一意性を証明します。
群の公理 :各元の逆元は唯一
g∈G について、
x∈G が xg = gx = e を満たしたとします。
このような x が少なくとも一つ G の中に存在することは、群の公理の [3] によって保証されています。
ここで、y∈G も、
yg = gy = e を満たしたとします。
そうすると、x = y となることが結論づけられてしまいます。
実際に、このことを見てみます。
y = ye = y(gx) です。
この右辺に [1] 結合律 を適用します。
すると、
y(gx) = (yg)x = ex = x となります。
よって、
y = y(gx) = x となります。
これで、g の G における逆元は全て x に一致するということを示すことができました。
すなわち、g の逆元は、x しかあり得ないという唯一性の証明となります。
これで、各 g∈G について、g の逆元が唯一であることが示せたので、g の逆元を表す記号を導入することができます。
g の唯一の逆元のことを g-1 と表すことにします。
ここまでのまとめ

【命題1】における単位元のことを e と表し、【命題2】における g の逆元のことを g-1 と表します。
抽象的な群 G なので、g-1 という g のインバースは、複素数体における零でない元の逆数のように分数というわけではありません。
しかし、g と g-1 での二項演算を計算した値が、必ず単位元 e となるというもので、群論の学習を進めるときに、よく使う内容となります。
二つ命題を証明しましたが、これらの証明部分を眺めていると、群の公理から無駄な内容を省けることが分かります。
群であることを示すためには、公理に示されている三つの条件を全て満たすことを確認するのですが、確認すべき内容を少し省くことができるというわけです。
ここまで、左かつ右単位元とか、左かつ右逆元と述べてきましたが、どちらも右だけで確認しておけば、必然的に左の単位元と左の逆元になっているということが導かれます。
群の公理 :条件を軽くできる
【命題3】
二項演算が定義されている空でない集合 G が、次の三つの条件を満たせば、群の公理を満たす。
① 結合律を満たす
② 右単位元 a をもつ
③ G の各元には右逆元が存在する
(各 g∈G に対し、gy = a)
②と③が、左単位元と左逆元ということを省いた条件になっています。
右単位元と右逆元についてだけ考えると良いということなので、群の公理を確認するときに、役立ちます。
【命題3】のおかげで、左単位元ということと、左逆元であることが自動で導かれるというわけです。
では、どうして左の方が自動で導かれるアルゴリズムの部分となる証明を、これから述べます。
<証明>
a∈G が、任意の h∈G に対し、
ha = h を満たす、つまり a が条件②の右単位元だとします。
そして、各 g∈G が与えられたときに、条件③から、g の右逆元 y∈G が存在します。
つまり、gy = a …★
今、y = ya = y(gy) となっています。
さらに、①の結合律から、
y(gy) = (yg)y なので、
y = (yg)y …(1)
ここで、y∈G に対して、条件②から y の右逆元 z が存在します。
そのため、
y(za) = (yz)a
= aa = a …(2)
(1) の両辺について、za と二項演算を計算します。
すると、
y(za) = ((yg)y)(za) となります。
(2) から、左辺の値は a なので、
a = ((yg)y)(za) …(3)
右辺について、一般の結合律から、括弧のつけ方に依らずに値が一つに決まるということを利用します。
すると、
((yg)y)(za) = (yg)(y(za)) となります。
再び (2) から、
y(za) = a なので、
((yg)y)(za) = (yg)a
= yg となります。
これで (3) の右辺を置き換え、
a = yg を得ます。
★から、gy = a でした。
つまり、
yg = gy = a …■
さらに、a が左単位元となっていることを示すと、■から y が g の左かつ右逆元となっているということになります。
そこで、任意の h∈G に対して、ah の値を計算します。
■の g として、
この h を考えると、
yh = hy = a を満たす y∈G が存在します。
そのため、
ah = (hy)h = h(yh)
= ha となります。
a は G における右単位元だったので、ha の値は h です。
ゆえに、
ah = ha = h です。
これは、a が左単位元であることを示しています。
これで、■から y が左かつ右逆元ということにもなります。【証明完了】
この証明ですが、途中までで一つの結果を導いておき、その結果を再び用いています。
すべてを記述すると長くなるので、区切りをつけて結果を導いておき、何度も使うというのも数学の証明では、よく使う手となります。
いずれにせよ、【命題3】から、群の公理を確認するときに、右単位元と右逆元について確認しておくと、自動的に左単位元と左逆元もカバーしてくれるので、役立ちます。
具体的な例で、群の公理を確認してみます。
具体例で実践
M(2, C) を複素数を成分とする2行2列の正方行列全体とします。
A∈M(2, C) について、
|A| を A の行列式とします。
{A∈M(2, C) | |A| ≠ 0} を G と置くと、G は群の公理を満たします。
このことを確認してみます。
【命題3】から、右単位元と右逆元についてのみ確認すれば良いので、少し気分が楽になります。
行列の乗法について、結合律が成立するので、【命題3】の②右単位元と③右逆元について確認します。
E を 2 次単位行列とすると、
|E| = 1 ≠ 0 なので、
E ∈ G となっています。
任意の A ∈ G に対して、
AE = A なので、E は G における右単位元となっています。
また、B ∈ G とすると、
|B| ≠ 0 より、
B は可逆行列なので、
B-1 が存在します。
そして、|B-1| の値は、|B| という複素数の逆数になるので、0 ではありません。
そのため、B-1∈ G です。
よって、BB-1 = E なので、B-1 は B の右逆元となっています。
これで、【命題3】の三つの条件を満たしたので、群の公理を満たすということになります。
この G を2次の一般線形群といいます。
行列論についての内容を使ったので、あまり【命題3】のありがたみが分かりづらいですが、右だけを注意しておけば良いという雰囲気さえ持って頂ければと思います。
次の命題では、【命題3】から、スムーズに結論が導かれることが分かります。
ちょっとした命題を証明
【命題4】
群 G の元 g について、
(g-1)-1 = g である。
【証明】
群の右逆元と左逆元が一致しているので、
g-1g = e です。
これは、g が g-1 の右逆元ということを示しています。
G の各元について、【命題3】より、右逆元と左逆元は一致していて、ただ1つしか存在しないことになります。
よって、(g-1)-1 = g です。【証明完了】
群の公理というと難しそうな雰囲気ですが、実は中学一年のときから群を具体的に知っています。
実数全体を R とすると、通常の加法という演算について R は群となっています。
【関連する記事】
部分群については、部分群の判定方法という記事で定義と同値な書き換えについて解説をしています。
具体的な群については、3次対称群という記事で、群の公理を満たす群について、写像の性質を使う練習を解説しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。