べき零群 – 中心列 | 降中心列と昇中心列への理解を整えて理解する準備を整える

2023年8月23日

群論入門で" べき零群 “を学習するときに、" 中心列 “や降中心列と昇中心列が出てきます。

この中心列についての基礎的な内容を理解できると、ベキ零群についての学習が始められます。

群論入門の終盤のこの内容を、きっちりと押さえておくと、数学科の３年次の代数の講義の単位の取得が見えてくるかもしれません。

三つの種類の列を理解するためには、交換子についての基礎内容を使います。

まずは、降中心列から説明します。

べき零群 – 中心列 :降中心列の定義

群 G について、これから降中心列の定義をします。

その際に、H, K がともに G の正規部分群であるとき、
交換子群 [H, K] という G の正規部分群を使います。

※ 交換子群という記事で、これが正規部分群であることを解説。

これら H, K の部分に、部分群を帰納的に定義して、降中心列を定義します。

群 G について、C₁(G) = G と定めます。

そして、自然数 i について、
C_i+1(G) = [G, C_i(G)] と定義します。

すると、帰納法より、各自然数 n について、
C_n(G) は G の正規部分群となります。

先ほどの交換子群の H と K として、
G と C_i(G) を使い、帰納的に定義するわけです。

【命題１】

群 G について、任意の自然数 n に対して、
C_n(G) は G の正規部分群である。

＜証明＞

n = 1 のとき、C₁(G) = G は、G の正規部分群です。

n = i ≧ 2 について、
C_i(G) が G の正規部分群と仮定します。

すると、G と C_i(G) が G の正規部分群なので、
交換子群についての一般論から、
[G, C_i(G)] は G の正規部分群です。

つまり、C_i+1(G) = [G, C_i(G)] は G の正規部分群です。 ■

さらに、各自然数 n について、包含関係が成立しています。

降下する包含関係の証明

【命題２】

群 G と任意の自然数 n について、
C_n(G) ⊃ C_n+1(G) である。

＜証明＞

【n = 1 のとき】

C₁(G) = G なので、
C₁(G) ⊃ C₂(G) となり、成立しています。

【n = i のとき】

C_i(G) ⊃ C_i+1(G) であると仮定します。

すると、
C_i+2(G) = [G, C_i+1(G)]
⊂ [G, C_i(G)] = C_i+1(G) です。

つまり、C_i+1(G) ⊃ C_i+2(G) です。

以上より、任意の自然数 n に対して、
C_n(G) ⊃ C_n+1(G) です。 ■

これで、
G = C₁(G) ⊃ C₂(G) ⊃ … ということが分かりました。

そして、【命題１】から、
各 C_i(G) は G の正規部分群です。

この正規部分群の列のことを降中心列といいます。

【命題１】と【命題２】を合わせると、
C_i(G)/C_i+1(G) ⊂ Z(G/C_i+1(G)) となります。

任意の g∈G と h∈C_i(G) に対して、
ghg^-1h^-1 = [g, h]
∈[G, C_i(G)] = C_i+1(G) です。

そのため、次のようになります。

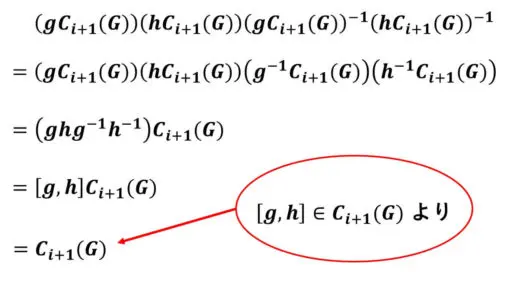
C_i+1(G) は G/C_i+1(G) の単位元なので、
(gC_i+1(G))(hC_i+1(G)) = (hC_i+1(G))(gC_i+1(G))

これは、hC_i+1(G) が G/C_i+1(G) の任意の元と可換であることを示しています。

よって、C_i(G)/C_i+1(G) ⊂ Z(G/C_i+1(G))

次に、昇中心列について説明します。

中心列 :昇中心列について

群 H があったときに、
{h∈H | hg = gh (∀g∈H)} = Z(H) を H の中心といいます。

H/N という剰余群についても、
Z(H/N) で、H/N の中心を表します。

ここから、昇中心列を定義するときに使うものたちの記号を定義します。

群 G が与えられたときに、
Z₀(G) = {e}, Z₁(G) = Z(G) と定義します。

※ e は群の単位元です。

そして、自然数 i に対し、
Z_i+1(G) = {g∈G | gZ_i(g)∈Z(G/Z_i(G))} と定義します。

例えば、Z₂(G) だと、G の元 g で、
gZ(G) が、剰余群 G/Z(G) の中心の元であるをすべて集めたものです。

Z₁(G) = Z(G) なので、
g∈Z₂(G) ということは、
gZ₁(G) が G/Z₁(G) の中心の元となっているということです。

このとき、
Z₂(G)/Z₁(G) は、Z(G/Z₁(G)) と一致しています。

また、Z₁(G) = Z(G) の各元を h とすると、
hZ₁(G) = Z₁(G) は、
G/Z₁(G) の単位元なので、
hZ₁(G)∈Z(G/Z₁(G)) となっています。

そのため、Z₂(G) の定め方から、
Z₁(G) ⊂ Z₂(G) となっています。

また、G の単位元 e は、G のどの元とも可換なので、
Z₀(G) = {e} ⊂ Z(G) = Z₁(G) です。

すなわち、
Z₀(G) ⊂ Z₁(G) ⊂ Z₂(G) となっています。

ここで、帰納的に Z_i(G) を定義したことから、帰納法で、次のような上昇列となっていることが分かります。

帰納的に上昇列を確認

【命題３】

群 G と任意の非負整数 n に対して、
Z_n(G) ⊂ Z_n+1(G) である。

＜証明＞

n = 0 のときに成立していることを既に確認しました。

n = i のときに、
Z_i(G) ⊂ Z_i+1(G) が成立していると仮定します。

すると、Z_i+1(G) の任意の元 h 対して、
hZ_i+1(G) = Z_i+1(G) は、
剰余群 G/Z_i+1(G) の単位元なので、
hZ_i+1(G)∈Z(G/Z_i+1(G)) です。

よって、Z_i+2(G) の定め方から、
h∈Z_i+2(G) です。

すなわち、Z_i+1(G) ⊂ Z_i+2(G) ■

これで、
{e} = Z₀(G) ⊂ Z₁(G) ⊂ Z₂(G) ⊂ … という上昇列ができていることが確認できました。

各 Z_i(G) が G の正規部分群となっていることを次に示します。

帰納的に順に確認

【命題４】

群 G と任意の非負整数 n に対して、
Z_n(G) は G の正規部分群である。

＜証明＞

n = 0 のとき、Z₀(G) = {e} は、G の正規部分群なので、成立しています。

n = i ≧ 0 のとき、
Z_i(G) が G の正規部分群だと仮定します。

x∈Z_i+1(G), g∈G を任意に取ります。

yZ_i(G)∈G/Z_i(G) を任意の元として、
(gxg^-1)Z_i(G) が、yZ_i(G) と可換であることを示します。

xZ_i(G) は G/Z_i(G) の中心の元なので、
xZ_i(G) は G/Z_i(G) の任意の元と可換であることを利用します。

(gxg^-1)Z_i(G)
= (gZ_i(G))(xZ_i(G))(g^-1Z_i(G))
= (xZ_i(G))(gZ_i(G))(g^-1Z_i(G))
= xZ_i(G) となっています。

よって、
((gxg^-1)Z_i(G))(yZ_i(G))
= (xZ_i(G))(yZ_i(G))
= (yZ_i(G))(xZ_i(G))
= (yZ_i(G))((gxg^-1)Z_i(G))

すなわち、
(gxg^-1)Z_i(G)∈Z(G/Z_i(G)) です。

(gxg^-1)Z_i(G) が G/Zi(G) の中心の元なので、
z_i+2(G) の定め方から、
gxg^-1∈Z_i+2(G) です。

したがって、
Z_i+2(G) も G の正規部分群です。

以上より、帰納法から、
群 G と任意の非負整数 n に対して、
Z_n(G) は G の正規部分群です。 ■

これで、
{e} = Z₀(G) ⊂ Z₁(G) ⊂ Z₂(G) ⊂ … という上昇列について、各 Z_i(G) が G の正規部分群となっていることが確認できました。

この上昇列を G の昇中心列といいます。

中心列 :三つの列の関係

群 G の正規部分群の列があったとします。

G = G₀ ⊃ G₁ ⊃ … ⊃ G_r = {e}

0 ≦ i ≦ r－1 のそれぞれについて、
G_i/G_i+1 ⊂ Z(G/G_i+1) であるとき、この列を G の中心列といいます。

このため、中心列は特別な正規列のことです。

G_i-1/G_i ⊂ Z(G/G_i) は、[G, G_i-1] ⊂ G_i と同値です。

同値であることを確かめます。

G_i-1/G_i ⊂ Z(G/G_i) とすると、
g∈G, h∈G_i-1 に対して、
(ghg^-1h^-1)G_i
= (gG_i)(hG_i)(gG_i)^-1(hG_i)^-1
= (hG_i)(gG_i)(gG_i)^-1(hG_i)^-1
= (hG_i)(hG_i)^-1 = G_i

そのため、ghg^-1h^-1∈G_i です。

つまり、[g,h]∈G_i となり、
[G, G_i-1] の生成元がすべて G_i に含まれているので、
[G, G_i-1] ⊂ G_i と分かります。

逆に、[G, G_i-1] ⊂ G_i とすると、
g∈G, h∈G_i-1 に対して、
ghg^-1h^-1∈G_i だから、
(ghg^-1h^-1)G_i = G_i です。

(gG_i)(hG_i)(gG_i)^-1(hG_i)^-1 = G_i だから、
両辺に右から (hG_i)(gG_i) を掛けると、
(gG_i)(hG_i) = (hG_i)(gG_i) となります。

つまり、hG_i は G/G_i の任意の元と可換なので、
hG_i∈Z(G/G_i) です。

ここまでで、降中心列と昇中心列と中心列という三つの列が出てきました。

降中心列だと、
各 C_i(G)/C_i+1(G) は Z(G/C_i+1(G)) に含まれるので、有限の長さで単位元に辿り着くと、中心列ということになります。

昇中心列については、
各 Z_i+1(G)/Z_i(G) が Z(G/Z_i(G)) に含まれるので、有限の長さで全体 G に辿り着くと中心列ということになります。

これら三つの列の関係についての定理を証明します。

降中心列と中心列

【定理１】

群 G の中心列を、
G = G₀ ⊃ G₁ ⊃ … ⊃ G_r = {e} とする。

このとき、0 ≦ i ≦ r について、
C_i+1(G) ⊂ G_i である。

＜証明＞

i = 0 のときは、
C₁(G) = G = G₀ より成立しています。

i = k ≦ r－1 のとき、
C_k+1(G) ⊂ G_k と仮定します。

C_k+2(G) = [G, C_k+1(G)]
⊂ [G, G_k]

また、中心列の定義から、
[G, G_k] ⊂ G_k+1 です。

すなわち、C_k+2(G) ⊂ G_k+1 となります。

このため、帰納的に、
0 ≦ i ≦ r のとき、
C_i+1(G) ⊂ G_i が示せました。 ■

この【定理１】から、群 G が中心列をもつと、
n ≧ r+1 について、
C_n(G) ⊂ C_r+1(G) ⊂ G_r = {e} となります。

このため、降中心列は、r+1 番目以降の項が確実にすべて単位群となっています。

つまり、群 G が中心列をもつならば、降中心列が有限の長さで単位群に到達するということです。

降中心列が有限の長さで単位群に到達するということは、降中心列が中心列の定義を満たすことになります。

よって、【定理１】から次の【定理１’】を得ます。

次は、昇中心列について、同じようなことを考えます。

昇中心列と中心列

【定理２】

群 G の中心列を、
G = G₀ ⊃ G₁ ⊃ … ⊃ G_r = {e} とする。

このとき、0 ≦ i ≦ r について、
G_r-i ⊂ Z_i(G) である。

＜証明＞

i = 0 のとき、
Z₀(G) = {e} なので、
G_r = {e} ⊂ Z₀(G) だから、成立しています。

i = k ≦ r－1 について、
G_r-k ⊂ Z_k(G) と仮定します。

中心列の定義から、
[G, G_r-k-1] ⊂ G_r-k です。

ゆえに、[G, G_r-k-1] ⊂ Z_k(G) となっています。

そのため、任意の h∈G_r-k-1, g∈G に対して、
(ghg^-1h^-1)Z_k(G) = Z_k(G) です。

よって、剰余群 G/Z_k(G) において、
(gZ_k(G))(hZ_k(G)) = (hZ_k(G))(gZ_k(G))

ゆえに、hZ_k(G) は G/Z_k(G) のすべての元と可換です。

つまり、
hZ_r-k(G)∈Z(G/Z_r-k(G)) です。

Z_k+1(G) の定め方より、
h∈Z_k+1(G) です。

つまり、
G_k+1 ⊂ Z_k+1(G) です。

以上より、帰納的に、
0 ≦ i ≦ r について、
G_r-i ⊂ Z_i(G) です。 ■

この【定理２】から、群 G が中心列をもてば、昇中心列が有限の長さで G に到達するということになります。

i = r のとき、
G = G₀ ⊂ Z_r(G) となるということです。

Z_r(G) ⊂ Z_r+1(G) ⊂ Z_r+2(G) ⊂ … なので、
r 以降の項は、すべて G と等しいです。

この昇中心列を次のように眺めます。

G = Z_r(G) ⊃ Z_r-1(G) ⊃ … Z₀(G) = {e} と、全体から単位群へという見方をします。

すると、それぞれの隣接する二項について、
Z_i(G)/Z_i+1(G) ⊂ Z(G/Z_i(G)) だったので、
昇中心列が中心列となっていることが分かります。

そのため、【定理２】から次の【定理２’】を得ます。

これで、【定理１’】と【定理２’】によって、中心列をもつことを有限の長さの降中心列や昇中心列で書き換えることができるということが分かりました。

ちなみに、群 G が中心列をもつとき、G を冪零べきれい群といいます。

関連記事として、可解群という記事も投稿しています。

これで今回の記事を終了します。

読んで頂き、ありがとうございました。