ブロック行列 積 | 区分行列を土台にするために

2022年1月6日

" ブロック行列 積 “に関して、ブロック分割された区分行列について、線形代数学の学習ですぐに使う定理を書いています。

その定理から、正方行列が逆行列をもつことと連立方程式が、どのように関連するのかということを解説します。

ブロック分割（区分行列）についての定理を使って、「正方行列が逆行列をもつこと」と「連立方程式」の関連を、線形代数学で学習します。

ブロック分割された行列の積を考えるときに、適切な分割が大切になります。

ブロック行列 :区分行列を認識

m × n 型行列 A = (a_ij) を図のように、図のように st 個のより小さいサイズの行列に分割して考えることをブロック分割といいます。

このブロック分割された行列 A のことを区分行列といいます。

たとえば、この図で、上から 2 番目で左から 1 番目の A₂₁ のことを、(2, 1) ブロックといいます。

より一般的に、上から i 番目で左から j 番目の (i, j) ブロックは、A_ij です。通常の行列の成分にあたるものがブロックになっています。

この区分行列を A = (A_ij) と表すことにします。

行列の成分と区別をするために、大文字と添え字で (i, j) ブロックを表すことが多いかと思います。

ここで、行列計算をするときに、(i, j) ブロックに使われている行列のサイズを押さえておく必要があります。

A₂₁ のサイズは、m₂ × n₁ 型行列となっています。

区分行列どおしで加法を計算するときに、各ブロックに使われている行列のサイズが然るべきサイズになっている必要があります。

ここから、ブロック分割された行列と加法について解説します。

区分行列どおしの加法

A = (A_ij) と B = (B_ij) という区分行列について、どの (i, j) ブロックについても、使われている行列 A_ij と B_ij が同じサイズのときに加法が計算されます。

つまり、A + B という行列もブロック分割され、(i, j) ブロックが A_ij と B_ij の和となります。

A + B = (A_ij + B_ij)

区分行列 A と区分行列 B で、あるブロック (p, q) について、A_pq と B_pq のサイズが異なっていたとします。

すると、A_pq + B_pq の値がエラーということになってしまいます。行列の加法は、同じサイズの行列どおしで定義されています。

これが、ブロック分割された区分行列どおしの加法についての定理です。

表現行列は、線形変換を表す行列です。

行列を調べることで、線形変換について分かることがあるので、行列を調べるときの手段の一つとして、ブロック分割を押さえておくと良いかと思います。

次に、証明が複雑になるけれども、線形代数学を学習するときに、よく出てくるブロック分割と乗法についての定理です。

ブロック行列 積 :区分行列どおしの乗法

【定理】
l × m 型行列 A, m × n 型行列 B に対して、それぞれのブロック分割について、次のようになっていたとします。

A_ij は l_i ×m_j 型行列、B_jk は m_j × n_k 型行列で、
l₁ + l₂ +・・・ + l_s = l,
m₁ + m₂ +・・・ + m_t = m,
n₁ + n₂ +・・・ + n_u = n とします。

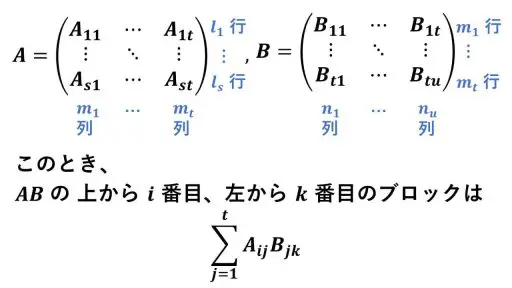
この結論の (i, k) ブロックの行列が、シグマを使った行列で表されています。

ちなみに、シグマ記号の上の自然数 t は、A のどの行についても、(*, l₁) から (*, l_t) ブロックまであるので、t です。

そして、この t は、B のどの列についても 、(m1, *) ブロックから (m_t, *) ブロックまであるので、t となっています。

これは、ブロック分割のそれぞれのブロックに配置されているのが行列です。

その状態で、通常の行列の成分であるかのように思って、乗法を計算できるというのが、この定理の良いところです。

ちなみに、行列の乗法が定義できるときには、サイズに条件がありました。

左の行列の列数と、右に行列の行数が同じになっていないといけませんでした。

この定理の仮定が、まさに、この条件を満たすように設定されています。

A_ij と B_jk について、列数と行数を定理の仮定に基づいて確かめてみます。

A_ij は l_i ×m_j 型行列だったので、列数は m_j です。一方、B_jk は m_j × n_k 型行列だったので、行数は m_j です。

これで、シグマ計算に現れる各項について、左の行列の列数と右の行列の行数が等しいので、確かに行列の乗法が計算できるということが確かめられました。

さらに、シグマ計算ですから、各項として現れる行列のサイズがすべて同じでなければ、加法が計算できません。

これについても確認をしておきます。

i と k を固定すると、1 以上 t 以下のどの自然数 j についても、A_ijB_jk のサイズは、m_i × n_k です。

よって、シグマの計算で使われる変数 j が 1 から t までの自然数を動くときに、現れる各項の行列のサイズはすべて、 m_i × n_k となっています。

これで、(i, k) ブロックにおいて、シグマ計算ができることが確認できました。

より明確に可視化するのも大切

この定理の結論が、文章になっているので、より見やすくするために、可視化しておきます。

この左辺の行列と、右辺の行列が一致しているというのが、定理の内容です。

右辺の各ブロックが定義できるように、分割の仕方に仮定がついているというわけです。

区分行列の乗法についての定理の証明

証明は、まず、左辺と右辺の行列のサイズが同じであることを確認します。

それから、左辺の (p, q) 成分が、右辺の (p,q) 成分と一致することを示せば、証明が完了します。
※ AB は l × n 型行列なので、p は 1 以上 l 以下の任意の自然数で、q は 1 以上 n 以下の任意の自然数で示すことになります。

まず、左辺の AB のサイズは、l × m 型行列と m × n 型の行列の乗法なので、l × n 型行列です。

次に、右辺のサイズを確認します。

A_1jB_j1 のサイズは l₁ × n₁ 型
・・・
A_sjB_j1 のサイズは ls × n₁ 型 となっています。

右辺の行列の (1, 1) ブロックから (s, 1) ブロックについて、成分についての行数は、仮定より、
l₁ + l₂+ ・・・ + l_s = l です。

左から 1 列目について行数をみましたが、左から u 列目までのどの列目についても、同じく行数は l となっています。

列数についても、同様に、
n₁ + n₂・・・ + n_u = n なので、右辺の行列の列数は n です。

これで、左辺と右辺が同じサイズの行列であることが確認できました。

AB の (p, q) 成分の値は、行列の乗法の定義から、
a_p1b_1q + a_p2b_2q + ・・・ + a_pmb_mq です。

※ 行列の基本的な計算については、対称行列と交代行列というブログで説明をしています。

また、左辺と右辺の行列のサイズは、(p, q) 成分は、右辺のある (i, k) ブロックの行列の中の成分です。

右辺の (i, k) ブロックは、
Σ_j=1t AijBjk です。

この A_i1B_1k+A_i2B_2k+…+A_itB_tk の
(p, q) 成分は、
Σ_j=1m(1) a_pjb_jq+Σ_j=m(1)+1m(2) a_pjb_jq+…+Σ_j=m(t-1)+1m(t) a_pjb_jq です。

仮定より、
m(1)+m(2)+…+m(t) = m だから、
a_p1b_1q + a_p2b_2q + ・・・ + a_pmb_mq となっています。

ゆえに、左辺と右辺の (p, q) 成分は、一致しました。

＜注意＞
A_i2B_2k について、シグマ記号の下が、j = m(2) から始まっていました。

これは、それぞれの行列のサイズを確認すると分かります。

A_i2 は l_i × m(2) 型で B_2k は m(2) × n_k 型です。

そのため、A_i2B_2k は l_i × n_k 型です。この A_i2B_2k の中の (x, y) 成分は、A_i2 の x 行目と B_2k の y 列目を使ったシグマ計算となります。

このときに、A_i2 の列数、もしくは B_2k の行数は、どちらも m(2) となっています。

行列 A の列数について、1 行目から m(1) 行目の次が、(m(1)+ 1) 行目で、順に m(2) 行目まで続いています。

このため、上で書いたシグマ記号の下が j = m(1)+ 1 で、シグマ記号の上が m(2) となっています。

そして、(x, y) 成分として、(p, q) 成分を考えているということから、シグマ計算で加法を計算する項を a_pjb_jq としています。

他のシグマ計算も A_itB_tk まで、同じ要領です。

ブロック分割と列ベクトル

行列 A を l × m 型行列とし、b₁, b₂, ・・・, b_n をそれぞれ m × 1 型行列（列ベクトル）とします。

ここで、(b₁, b₂, ・・・, b_n) というブロック分割を考えます。

(1, 1) ブロックは m × 1 型行列で、(1, 2) ブロックから順に (1, n) ブロックまで同様のサイズの列ベクトルが並んでいます。

よって、(b₁, b₂, ・・・, b_n) は、m × n 型行列となっています。

A 自身も、(1, 1) ブロックだけにブロック分割されていると考えます。

そうすると、A は l × m 型なので、行列の乗法が計算できます。

A(b₁, b₂, ・・・, b_n) は、l × n 型行列となっています。

ここで、1 以上 n 以下の 自然数 i について、A の列数と b_i の行数がどちらも同じことから、Ab_i という乗法が計算できます。

それぞれの列ベクトルについて、どの i についても、Ab_i は l × 1 型の行列になっています。

ここで、先ほどの区分行列の乗法についての定理を適用すると、次のようになります。

A(b₁, b₂, ・・・, b_n)
= (Ab₁, Ab₂, ・・・, Ab_n)

この等式は、線形代数学を学習するときに、よく使われるかと思います。

乗法を計算するときに、右の行列を列ベクトルたちでブロック分割をしておいて、左の行列 A をあたかもスカラーであるかのように変形しています。

この変形が、正方行列が逆行列をもつことから、連立方程式へとつなげるときに役立ちます。

ブロック分割 :逆行列をもつとき

ここで、使う記号を設定しておきます。自然数 n について、E_n を n 次の単位行列とします。

この単位行列は、対角成分といって、(1, 1) 成分、(2, 2) 成分 から順に (n, n) 成分が 1 で、これらの対角成分でない成分が 0 となっている行列です。

つまり、(i, j) 成分について、i = j のとき 1 で、i ≠ j のとき 0 という行列です。

1 以上 n 以下の自然数 k について、
e_k を n × 1 型行列で、(k, 1) 成分が 1 で、他の成分がすべて 0 である列ベクトルとします。

これら e₁, e₂, ・・・, e_n を使って、単位行列 E_n をブロック分割します。

E_n = (e₁, e₂, ・・・, e_n) となります。

n × n 型行列 A、つまり、n 次正方行列 A が正則であるとは、A が逆行列をもつことです。
※ 一般に A^－1 で A の逆行列を表します。

AX = E_n となるときに、この n 次正方行列 X を A の逆行列といいます。

ここで、A = (a_ij) とします。これは、 A の (i, j) 成分が a_ij ということです。

そして、逆行列 X =(x_ij) をブロック分割します。

y_k を X の k 列目を列ベクトルとしたものとします。

すなわち、y_k の (1, k) 成分が x_1k ,・・・, (n, k) 成分が x_nk です。

すると、AX = E_n は次のようになります。

A(y₁, y₂, ・・・, y_n)
= (e₁, e₂, ・・・, e_n)

ここで、左辺について、ブロック分割の乗法についての定理を適用すると、次のようになります。

(Ay₁, Ay₂, ・・・, Ay_n)
= (e₁, e₂, ・・・, e_n)

この左辺と右辺の行列の成分を比較すると、次の等式が得られます。

Ay₁ = e₁, Ay₂ = e₂, ・・・, Ay_n = e_n

連立方程式が見えてきました

A = (a_ij), y_k は X =(x_ij) の k 列目を列ベクトルとしたものということから、得られた n 個の行列について、左辺と右辺の成分を比較します。

各 k について、Ay_k の (p, 1) 成分は、

a_p1x₁₁ + a_p2x₂₁ + … + a_pnx_n1 となっています。

Ay_k = e_k ですから、(k, 1) 成分が 1 で、他の成分は 0 となっています。

よって、p = k のときには、

a_p1x₁₁ + a_p2x₂₁ + … + a_pnx_n1 = 1 です。
　
p ≠ k のときには、

a_p1x₁₁ + a_p2x₂₁ + … + a_pnx_n1 = 0 です。
　
k について、1 から n まであるので、連立方程式となっています。

これらの考察から、AX = E_n ということは、連立方程式が解をもつということになります。

逆に、

Ay₁ = e₁,
Ay₂ = e₂,
・・・
Ay_n = e_n

という連立方程式が解をもつと、上で書いた考察を逆に辿ります。

そして、(y₁, y₂, ・・・, y_n) という連立方程式の解を成分とする行列を X とすると、A の逆行列が得られるわけです。

ブロック分割の乗法についての定理で、

(Ay₁, Ay₂, … , Ay_n)
= (e₁, e₂, … , e_n)

と等号なので、逆に辿れることが効いています。

したがって、連立方程式が解けるということは、A の逆行列 X を作れるということになります。

連立方程式を解くために

n 次正方行列の逆行列が存在するということは、上で書いた連立方程式が解ければ良いということになります。

では、どうやって連立方程式を解くのかということですが、それには、行列の基本変形という操作を使います。この操作を使って、連立方程式から逆行列を作る方法が、掃き出し法という方法です。

ブロック分割を使って、なんで連立方程式を解くことが、行列の逆行列を求めることかということまで押さえておくと、線形代数学の理解が深まるかと思います。

もちろん、理論の部分は難しいので、まずは、とにかく掃き出し法を具体的に使えるように練習しておくのが良いかと思います。

そして、何度か抽象的な理論に向き合っていると、そのうち徐々に仕組みの部分が分かってくるかと思います。

このブロック分割の内容を使った理論の例として、行列の対角化があります。

ブロック分割をしてからの行列の乗法を理解していると、対角化についての理論の学習が分かりやすくなるかと思います。

また、線形写像に関する内容で、退化次数という値を求めるときにも、ブロック分割の内容を使っています。

これで、今回のブログ記事を終了します。

読んで頂き、ありがとうございました。