置換積分 | 公式の証明と理解しやすいような例題を用いての練習【数学III】

数学3の" 置換積分 “についての基本的な公式を導出することを解説しています。自分で公式を作れると、迷ったときに原点に立ち戻って考察を進められるので役立ちます。
x で微分すると、関数 f(x) となる関数のことを、f(x) の原始関数といいます。
f(x) の原始関数は、F(x) + C (C は定数) という形になっています。
これを f(x) の x についての不定積分といい、
∫ f(x) dx = F(x) + C と表します。
※ この C を積分定数といいます。
x について不定積分をしてから、x で微分をすると、もとの f(x) となるということを足掛かりにして、置換積分についての基本的な公式を導きます。
※ 目次の項目を選択すると該当箇所へ移動します。
置換積分 :置換積分法の公式の導出
置換積分についての基本となる公式を導くために必要な知識は、二つです。
① x で不定積分をしてから x で微分すると元の関数
② 合成関数の微分
合成関数の微分については、リンク先の記事で詳しく解説をしています。
原始関数と元の積分をされる被積分関数の関係に慣れるために、既に微分の単元で学習をした三角関数の微分を例にして述べておきます。
f(x) = cos x について、sin x を x で微分すると cos x となることから、f(x) の原始関数の一つが、sin x だと分かります。
定数の分だけズレることもできるので、不定積分をするときには、積分定数 C をつけます。
つまり、
∫ f(x) dx = ∫ cos x dx = sin x + C
よって、f(x) の原始関数の一つを F(x) と表すと、
F(x) = sin x で、
∫ f(x) dx = F(x) + C = sin x + C です。
よって、
d/dx(F(x)) = (sin x + C)’ = cos x = f(x) となっています。
この関係を基礎として議論を進めることになります。
dy/dt=dy/dx・dx/dt
合成関数の微分も使って、置換積分の公式を導出します。
x を使った式を t を使った文字で置換するため、x が t の関数という扱いになります。そうしたときに、合成関数の微分の考えが役立ちます。
では、ここまでの内容を使って、置換積分の公式を導きます。
関数 f(x) の原始関数の一つを F(x) とすると、
y = ∫ f(x) dx = F(x) + C となります。
この x が、微分可能である t の関数 g(t) を用いて表されているときに、置換積分の公式が導かれます。
x = g(t) で、g(t) が微分可能という設定で、以下の議論を進めます。
y は x の関数で、x は t の関数だから、合成関数の発想で、y が t の関数となっています。
そこで、y を t で微分します。
合成関数の微分の公式から、
dy/dt = dy/dx・dx/dt となります。
今、y = ∫ f(x) dx = F(x) + C なので、
dy/dx は、F(x) + C という f(x) の原始関数を x で微分したものです。
そのため、この記事の始めに述べた内容から、
dy/dx = (F(x) + C)’ = f(x) です。
また、x = g(t) という設定だったので、
dx/dt = g'(t) です。
これらを合成関数の微分の公式に代入すると、
dy/dt = dy/dx・dx/dt
= f(x)・g'(t) … ★ となります。
また、dy/dt という y を t で微分した導関数を t で不定積分すると、元の y に戻ります。
よって、★より
y = ∫ (dy/dt) dt = ∫ f(x)・g'(t) dt
さらに、x = g(t) だったので、
y = ∫ f(g(t))・g'(t) dt です。
y = ∫ f(x) dx だったので、左辺を書き換えると、
∫ f(x) dx = ∫ f(g(t))・g'(t) dt という置換積分の公式になります。
ここで、導いた置換積分の公式を使う簡単な例題で練習をすることにします。
置換積分 :例題で公式を使う練習
【例題1】
f(x) = x(x+3)1/2 を x について不定積分してください。
ルートをつけるということは、1/2 乗をするということになります。微分や積分をするときに、指数を分数で考えて計算をします。
先ほどの公式
「∫ f(x) dx = ∫ f(g(t))・g'(t) dt」で、何を f(x) と g(t) とするかによって、うまく計算できたり、計算できなかったりします。
自分で思考錯誤しながら、置換積分の式を作るつもりで計算に臨むように日頃から意識しておくと、大学受験レベルの置換積分も、できるようになってくるかと思います。
今回は、t = (x+3)1/2 と置いてみます。
ルートは正の平方根なので、その値は 0 以上の実数となっています。
そのため、今、t ≧ 0 です。
g(t) とは何か、そして f(g(t)) がどうなるのかを見定めて、置換積分の公式の通りに計算できれば完了です。
両辺を二乗することで、
t2 = x+3 となります。
よって、x = t2-3 となります。
これで、x = g(t) = t2-3 となりました。しかも、g(t) は t で微分可能な関数です。
微分すると、g'(t) = 2t … (1)
また、x = g(t) なので、これを f(x) に代入して、f(g(t)) を計算します。
f(g(t)) = (t2-3)(t2-3+3)1/2
= (t2-3)(t2)1/2 です。
t ≧ 0 だったので、(t2)1/2 = t となっています。
これより、
f(g(t)) = t(t2-3) = t3-3t … (2)
(1), (2) を代入することで、
∫ f(x) dx = ∫ f(g(t))・g'(t) dt の右辺が計算できます。
∫ f(x) dx = ∫ (t3-3t)・2t dt
= ∫ (2t4-6t2) dt
= 2/5t5-2t3+C
(ここで、C は積分定数です。)
t を元の (x+3)1/2 に戻します。ただ、スムーズに因数分解できるときは、因数分解をしたいので、t の状態で因数分解をした後で、t を x の式に戻すようにします。
t2 = x+3 を利用して、できるだけ 1/2 乗が絡まない計算を進めると楽です。
できるだけ整数係数で計算
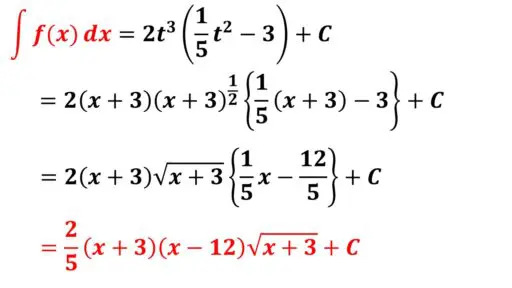
これで、求める不定積分を計算することができました。
できるだけ整数係数の式を因数とするようにすると、計算が楽になるときが多いです。
1/5 をくくり出して、
1/5x-12/5 = 1/5(x-12) とし、分数を先頭に掛ける形にしました。
また、t3 = (x+3)3/2 を指数法則で、
t3 = (x+3)(x+3)1/2 としました。
(x+3)1/2 が邪魔なので、掛け算をしたときに、右端に移動させました。
因数分解の仕方によって、見た目が違った式に見えることもあります。
ルートをつけることを 1/2 乗することとして計算することが多い数学3です。
高1のときの二重根号の外し方を、1/2 乗と考えて再び計算をしてみると、指数が分数のときの良い計算練習になるかと思います。
ここから、先ほど導いた置換積分の公式を書き換えることをします。
置換積分 :公式の書き換え
x の関数 f(x) について、x = g(t) としてから、
∫ f(x) dx = ∫ f(g(t))・g'(t) dt を導きました。
ここで、x に t を代入し、t に x を代入します。
t の関数 f(t) について、t = g(x) としてから、同様の議論をすることによって、
∫ f(t) dt = ∫ f(g(x))・g'(x) dx が導かれます。
左辺と右辺を入れ替えると、
∫ f(g(x))・g'(x) dx=∫ f(t) dt となります。
これが、書き換えをして作った置換積分の公式の変形版です。左辺から右辺へと計算を進めるときに使います。
今度は、この書き換えた方の公式を例題で練習してみます。
書き換えた公式の利用
【例題2】
∫ sin2xcos x dx を x について不定積分してください。
∫ f(g(x))・g'(x) dx=∫ f(t) dt の公式の形が、【例題2】の式を見たときに見えると、こちらを使うということが分かります。
f(t) が何か、g(x) はどうなっているのかということを調べてみます。
sin x を x で微分すると cos x となることから、
g(x) = sin x と考えると、
g'(x) = cos x です。
そうすると、f(g(x)) = sin2x ということから、
f(t) = t2 だと気づけます。
ある程度の合成関数についての慣れが必要になりますが、
t = g(x) = sin x と置くと、
f(t) = f(g(x)) = sin2x = t2 となっていることが分かります。
これで、書き換えて得られた方の公式が使えます。
∫ sin2xcos x dx
= ∫ f(g(x))・g'(x) dx
= ∫ f(t) dt = ∫ t2 dt
= 1/3t3+C
(ただし、C は積分定数)
t を元に戻すと、
∫ sin2xcos x dx = 1/3sin3x+C となります。
これで、答えが求まりました。
∫ f(g(x))・g'(x) dx=∫ f(t) dt の公式から、さらに数3でよく使う公式が導けます。
置換積分 :logが絡む公式
∫ f(g(x))・g'(x) dx=∫ f(t) dt … ■において、
f(t) = 1/t と置きます。
t = g(x) という実数を代入すると、
f(g(x)) = 1/g(x) です。
そのため、
f(g(x))・g'(x) = g'(x)/g(x) となります。
分子が g'(x) で、分母が g(x) となっています。
ここまでの内容を■に代入すると、次のようになります。
∫ f(g(x))・g'(x) dx = ∫ g'(x)/g(x) dx です。
また、∫ f(t) dt = ∫ 1/t dt = log|t|+C です。
(ただし、C は積分定数です。)
t = g(x) だったので、
∫ f(t) dt = log|g(x)|+C となっています。
■の公式から、
∫ f(g(x))・g'(x) dx = ∫ f(t) dt なので、
∫ g'(x)/g(x) dx = log|g(x)|+C を得ます。
この公式は、数3でよく使います。これを使った三角関数関連の有名な不定積分を例題として述べておきます。
∫tanx dxを計算する
【例題3】
∫ tan x dx を x について不定積分してください。
tan x = sin x/cos x = -(cos x)’/cos x です。
よって、g(x) = cos x とすると、
∫ tan x dx = -∫ g'(x)/g(x) dx
= -log|cos x|+C です。
(ただし、C は積分定数)
これで、∫ tan x dx = -log|cos x|+C と計算できました。
ここまで述べてきたように、置換積分を計算するときに、合成関数についての考え方が、よく使われています。そのため、合成関数についての定義や、合成関数の微分に慣れておくことが大切になります。
置換積分について述べてきましたが、部分積分についての記事も投稿しています。
数学3の積分で、置換積分と部分積分は基礎となる大切な内容になります。
微分の応用については、加速度ベクトルという記事を投稿しています。
この理論を基にして、
等速円運動という高校物理にも関連する内容とつながる内容を解説しています。
また、置換積分の公式から、
数2で学習した偶関数-奇関数についての定積分の公式が導けます。
これで今回の記事を終了します。
読んで頂き、ありがとうございました。