確率変数の独立 | 積についてE(XY)、和についてV(X+Y)の公式が独立だからこそ成立
" 確率変数の独立 “について、積に関しては、
E(XY) = E(X)E(Y) が成立します。
和に関しては、
V(X+Y) = V(X) + V(Y) となります。
X と Y が独立なときに成立する公式を押させることで、独立という状況が扱いやすくなります。
さらに独立と関係なく成立する公式と合わせて、
V(aX+bY) = a2V(X) + b2V(Y) も導きます。
記事の後半からは、事象の独立について解説をしています。
それでは、確率変数 X と Y が独立なときに、積 XY と和 X + Y に成立する公式について、解説します。
確率変数の独立 :積についてE(XY)
確率変数 X と Y について、X の取る値が a で、Y の取る値が b であるときに使う記号から説明します。
「X の値が a であり、かつ、Y の値が b となる確率」を表す記号を、
P(X =a, Y = b) と表します。
P(X = a) は、「X の取る値が a となる確率」で、
P(X = b) が、「Y の取る値が b となる確率」です。
確率変数 X と Y が互いに独立なとき、
P(X =a, Y = b)= P(X = a)P(X = b) となります。
P(X = a) と P(X = b) を掛け合わせるだけで良いので、独立なときは計算しやすくなります。
高校一年のときに、確率の単元で、二つの試行が独立ということを学習しました。片方の結果が、もう片方へ影響を及ぼさないことが試行の独立でした。
独立試行の確率について、確率どおしの積を計算しました。
同じ要領で、確率変数が独立なときは、
P(X = a) と P(X = b) を掛け合わせます。
確率変数 X と Y が独立なときに成立する公式について、確率変数の積 XY についての期待値に関する公式があります。
XYの値を論理的に観察
【X と Y が独立なとき】
確率変数 X が取る値が、x1, x2 だとします。
そして、それぞれが起こる確率が、
P(X = x1) = p1, P(X = x2) = p2 だとします。
確立変数 Y が取る値を y1, y2 とします。
そして、それぞれが起こる確率を、
P(Y = y1) = q1, P(Y = y2) = q2 とします。
X と Y が互いに独立なとき、期待値 E(XY) の値が、どうなっているのかを解説します。
X と Y について、それぞれの値が起こる確率が与えられている状況です。
そこで、X, Y の同時分布についての確率を考えます。
P(Y = y1) = q1 となるとき、次の場合が考えられます。
X = x1 の場合と X = x2 の場合が論理的に考えられます。
X と Y が互いに独立なので、
X = x1 かつ Y = y1 である確率は、
P(X = x1)P(Y = y1) = P(XY = x1y1) となっています。
P(X = x1) = p1, P(Y = y1) = q1 だったので、
XY の値が x1y1 である確率は、
P(XY = x1y1) = p1q1
Y = y1 のとき、X = x2 となる場合も考えられるので、XY の値が x2y1 となる確率も同様に計算できます。
P(XY = x2y1) =
P(X = x2)P(Y = y1) = p2q1
XY の期待値を求めるために、残りの可能性についても、起こる可能性を計算します。
Y = y2 のとき、
X = x1 または X = x2 です。
P(XY = x1y2) =
P(X = x1)P(Y = y2) = p1q2
Y = y1 かつ X = x2 のときも確率を計算します。
P(XY = x2y2) =
P(X = x2)P(Y = y2) = p2q2
これで、確率変数 XY が取る値と、それぞれの起こる確率を全て求めました。
ここまでの内容から、期待値を計算できます。
E(XY)を求める
XY の値が x1y1 となる確率は、
P(XY = x1y1) = p1q1 です。
XY の値が x2y1 となる確率は、
P(XY = x2y1) = p2q1
XY の値が x1y2 となる確率は、
P(XY = x1y2) = p1q2
XY の値が x2y2 となる確率は、
P(XY = x2y2) = p2q2
確率変数 XY の取る値と、その値となるときの確率を掛け合わせたものを全て足し合わせたものが、期待値の定義です。
したがって、
E(XY) = (x1p1+x2p2)(y1q1+y2q2)
= E(X)E(Y) となります。
このように、X と Y が互いに独立なとき、E(XY) は E(X) と E(Y) の積となっています。
【まとめ】
確率変数 X と Y が互いに独立なとき、
E(XY) = E(X)E(Y)
ちなみに、X と Y が独立であっても、独立でなくても、
E(X + Y) = E(X) + E(Y) となっています。
また、確率変数が X, Y, Z と三つあるときに、X, Y, Z が互いに独立であることの定義があります。
【定義】
確率変数 X, Y, Z について、X, Y, Z の取る任意の値をそれぞれ a, b, c とする。
P(X = a, Y = b, Z = c)
= P(X = a)P(Y = b)P(Z = c) が成立するとき、X, Y, Z が互いに独立であるという。
X, Y, Z が互いに独立であるときに、
期待値について、
E(XYZ) = E(X)E(Y)E(Z) が成立します。
それでは、X と Y が互いに独立であるとき、分散について役立つ公式を証明します。
確率変数の独立 :和についてV(X+Y)
【公式】
確率変数 X と Y が互いに独立なとき、
V(X + Y) = V(X) + V(Y)
この和についての分散の公式は、よく使います。
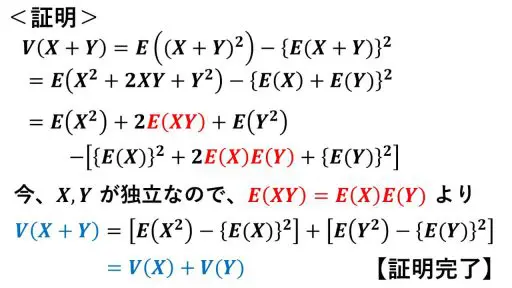
また、X と Y が独立であっても、独立でなくても、定数 t について、V(tX) = t2V(X) が成立します。
今、証明した公式と、V(tX) = t2V(X) を合わせると、次の公式が得られます。
V(aX+bY)の公式
【公式】
確率変数 X と Y が互いに独立であるとする。
a, b を定数とする。
このとき、
V(aX + bY) = a2V(X) + b2V(X)
＜証明＞
X と Y が独立なので、分散の和の公式から、
V(aX + bY) = V(aX) + V(bY)
さらに、V(aX) = a2V(X),
V(bY) = b2V(X) だから、
V(aX + bY) = a2V(X) + b2V(Y)【証明完了】
ちなみに、三つの確率変数 X, Y, Z が互いに独立なとき、定数 a, b, c について、
V(aX + bY + cZ) =
a2V(X) + b2V(Y) + c2V(Z) が成立します。
練習問題
【練習問題１】
表の出る確率が p (0 < p < 1) である百円玉を 2 回投げます。
1 回目に表が出たら X = 1,
1 回目に裏が出たら X = 0,
2 回目に表が出たら Y = 1,
2 回目に裏が出たら Y = 0
とすることにより、確率変数 X と Y を定義します。
a, b, c を p に無関係な定数とするとき、
Z = aX + bY + cXY という確率変数の期待値 E(Z) を求めてください。
＜解説と答え＞
1 × p + 0 × (1 － p) より、
E(X) = p, E(Y) = p です。
ここで、X と Y は独立だから、
E(Z) = E(aX + bY + cXY) =
aE(X) + bE(Y) + cE(XY)
さらに、X, Y が独立なので、
E(XY) = E(X)E(Y) より、
E(Z)= aE(X) + bE(Y) + cE(X)E(Y)
= ap + bp + cp2= cp2 + (a + b)p【答え】
もう一つ独立についての練習問題です。
【練習問題２】
X と Y が互いに独立な確率変数とします。
V(X) = 3, V(Y) = 4 のとき、
V(2X + 5Y) の値を求めてください。
＜解説と答え＞
X と Y が互いに独立なので、分散の和の公式から、
V(2X + 5Y) = 22V(X) + 52V(Y)
= 4×3 + 25×4 = 12 + 100 = 112【答え】
ここからは、よく似た名前ですが、内容が異なる数Bの確率の用語について説明をします。
事象の独立 :定義と記号
【定義１】
事象 A, B に対して、
P(A ∩ B) = P(A)P(B) が成立するとき、事象 A と事象 B が独立であると定義する。
A と B が独立でないときは、従属であると定義する。
つまり、
P(A ∩ B) ≠ P(A)P(B) のとき、A と B が従属であると定義する。
ここで、
P(A ∩ B) は、事象 A ∩ B が起こる確率を表しています。
P(A), P(B) についても、それぞれ事象 A, B が起こる確率を表す記号です。
P(A) ≠ 0, P(B) ≠ 0 のときは、
確率の乗法定義が成立するということです。
PA(B) = P(A)P(B),
PB(A) = P(B)P(A) = P(A)P(B) という条件付き確率で学習した内容です。
数学Bで学習するときには、条件付き確率の内容を理解していることを前提として議論が進みます。
ここで、ややこしいのが、確率変数を用いた内容が絡むことです。
日常語とのギャップ
独立ということについて、上で述べた確率変数の独立がありました。
高校数学の内容では、この二つは同値として扱われます。
同値ということは、書き換えが可能ということです。
そこで、二つの確率変数が独立ということの定義を見てみます。
【定義２】
ある試行において、確率変数 X と Y が取る値が、X が a で、かつ Y が b であるとする。
このとき、
P(X = a, Y = b) で X が a で、かつ Y が b である確率を表す。
そして、
a と b の値に関わらず、
P(x = a, Y = b)
= P(x = a)P(Y = b) となっているとき、二つの確率変数 X と Y が独立であると定義する。
「事象 A と事象 B が独立」ということと、「確率変数 X と Y が独立」ということが同値であると述べられることもあります。
「事象 A, B と対応する確率変数 X と Y の関係から」と、さらっとスルーされることが多いです。
この言い方ですが、分かったようで分かりにくい内容です。
この部分に、具体例を使って切り込みます。
「対応する」という意味が、はっきりと述べられていないために、納得しようにも納得できないという状況です。
そこで、
X = a となるときの事象を A, Y = b となるときの事象を B と置くことにした上で、a と b の値に関わらず、
P(A ∩ B) = P(A)P(B) が成立すると考えます。
すると、これは、
P(X = a, Y = b)
= P(X = a)P(Y = b) と同じことを表します。
a と b の値に関わらず成立するということは、a と b として起こり得る全ての値について、それぞれの等式が成立するということです。
確率の記号を用いて押さえておくと、具体的に事象の独立を確かめられるようになります。
この内容ですが、
X = a, Y = b のときに、
それぞれそうなるときの事象を Aa, Bb と添え字をつけて表しておくと、どんな a と b が取る値に対しても等式が成立するということが分かりやすいかと思います。
試行の独立については、後で説明します。
まずは、事象の独立と確率変数の独立について、トランプを用いて様子を見ることにします。
J（ジャック）は 11,
Q（クイーン）は 12,
K（キング）は 13 として議論を進めます。
なお、エースも 1 として表すことにし、ジョーカーを考えない 52 枚のトランプを使います。
事象の独立 :トランプで考察
【設定】
52枚のトランプから 1 枚のトランプを選ぶという試行について、考えます。
ハート、スペード、クローバ、ダイヤの 4 種類のそれぞれについて、1 から 13 まであるという設定で 52 枚です。
同じ数字でも、種類によって異なる 1 枚と認識するために、記号をつけておきます。
(ハ, 1) だと、ハートのエースの 1 です。
同じく (ス, 1), (ク, 1), (ダ, 1) というように記号をつけます。
これで、同じ 1 でも、4 種類が区別できます。
一般に、
(ハ, i) で i = 1, … , 13 というように考え、全部で 52 枚のトランプ全体を全事象 U としておきます。
次に、確率変数 X を定義します。
取り出したトランプがハートのとき、
X に対して、1 を対応させます。
ハートではないトランプのときは、
X に対して、0 を対応させます。
これで、確率変数 X が取る値は、1 か 0 のいずれかということになります。
そして、確率変数 Y を定義します。
取り出したトランプの数字を Y の取る値と定義します。
これで、1 から 13 の 13 個の値を Y が取ることになります。
先ほど述べた事象の独立と、確率変数の独立について考えます。
事象の独立の例
X = 1 となるときの事象を A1 とします。
すると、X = 1 ということは、ハートの種類のトランプを取り出すということと同じになります。
Y = 13 となるときの事象を B13 とします。
確率の乗法定理の等式が成立することを確認します。
P(A1) は、ハートのトランプを取る確率です。
そのため、
P(A1) = 13/52 = 1/4 です。
P(B13) という 13（キング）を取り出す確率も求めます。
(ハ, 13), (ス, 13),
(ク, 13), (ダ, 13) の 4 つが条件を満たすトランプになります。
そのため、
P(B13) = 4/52 = 1/13 です。
ゆえに、
P(A1)P(B13) = 1/4 × 1/13
= 1/52 …(1)
P(A1 ∩ B13) は、取り出したトランプがハートであり、かつ 13 であるという確率です。
(ハ, 13) しか、この条件を満たさないので、
P(A1 ∩ B13) = 1/52 …(2)
(1) と (2) から、
P(A1 ∩ B13) = P(A1)P(B13) が成立しています。
より、一般的に、
1 ≦ i ≦ 13 である自然数 i について、
取り出したトランプの数字が i であるという事象を Bi とします。
全く同じ議論で、
P(A1 ∩ Bi) = P(A1)P(Bi) が成立します。
まだ、事象の独立は確かめられていません。
確率変数 X と Y が取り得る全ての値について、確率の乗法定理の等式が成立することを確かめて、はじめて定義に当てはまるということになります。
残りの可能性も確認する
X = 0 となるときの事象を A0 と表すことにします。
X = 0 は、ハートではない種類のトランプを取り出すということでした。
そのため、
P(A0) = 39/52 = 3/4 です。
1 ≦ j ≦ 13 である自然数 j について、
取り出したトランプの数字が j であるという事象を Bj とします。
P(Bj) = 4/52 = 1/13 です。
ゆえに、
P(A0)P(Bj) = 3/4 × 1/13
= 3/52 …(3)
P(A0 ∩ Bj) は、取り出したトランプの種類がハートではなく、かつ数字が j ということです。
(ス, j), (ク, j), (ダ, j) の 3 つが該当する場合です。
そのため、
P(A0 ∩ Bj) = 3/53 …(4)
(3) と (4) より、
P(A0 ∩ Bj) = P(A0)P(Bj) です。
これで、確率変数 X と Y が取り得る全ての値について、確率の乗法定理の等式が成立していることが確認できました。
よって、事象の独立が確認できました。
はじめに述べて定義では、
X = a となるときの事象を A, Y = b となるときの事象を B と置き、a と b が、どの値のときでも確率の乗法定義が成立するときに事象が独立と定義しました。
先ほどは、添え字を用いてA0 や A1 や Bi などと表しました。
この右下に添え字が書かれていなだけで、「どの値のときでも成立する」ということが認識しづらくなるので注意です。
今度は、この同じトランプの設定において、確率変数 X と Y が独立であることを確認します。
確率変数も考慮
1 ≦ i ≦ 13 を満たす自然数を i とします。
P(Y = i) を求めます。
数字が i であるトランプの種類は 4 種類でした。
そのため、
P(Y = i) = 4/52 = 1/13 です。
次に、X = 1 となる確率を求めます。
これは、ハートを取り出すということです。
そのため、
P(X = 1) = 13/52 = 1/4 です。
ゆえに、
P(X = 1)P(Y = i)
= 1/4 × 1/13
= 1/52
一方、P(X =1, Y = i) は、取り出したトランプがハートであり、かつ数字が i である確率です。
該当するのは、(ハ, i) の 1 枚のみです。
よって、
P(X =1, Y = i) = 1/52
= P(X = 1)P(Y = i) です。
また、X = 0 のときは、ハート以外の種類のトランプを取り出すということでした。
そのため、
P(X = 0) = 39/52 = 3/4 です。
これより、
P(X = 0)P(Y = i)
= 3/4 × 1/13
= 3/52 です。
P(X = 0, Y = i) は、取り出したトランプがハートではない種類で、かつ数字が i という確率です。
(ス, i), (ク, i), (ダ, i) の 3 枚が条件に該当します。
そのため、
P(X = 0, Y = i) = 3/52 です。
よって、
P(X = 0, Y = i) = 3/52
= P(X = 0)P(Y = i) です。
これで、確率変数 X と Y が独立であることの定義が確認できました。
「事象が独立」ということと「確率変数が独立」が同値と述べられることもあるということについて、具体例を用いて考察しました。
確かに表面的な記号の使い方に注意すると、本質的に同じ議論をしています。
しかし、この記事で述べてきたことは、離散型の確率変数についてのことです。
連続型の確率変数もあり、大学の数学では、もっと複雑で難しい内容を扱うことになります。
高校の数学では、離散型のシンプルな設定で同値と思っておくくらいにしておき、練習問題や大学で過去に出題をされた問題を通じて、事象の独立と確率変数の独立には、これくらいの例で触れておくと良いかと思います。
なお、一般に、事象の独立が成立していても、試行の独立が成立するとは限りませんので注意です。
「事象が独立」ならば、「試行が独立」は、一般的に成立するとは限らないという事実だけを述べるに留めておきます。
関連するブログ記事
単元のつながりを考え、学習を進めながら理解する理論の幅を広げていくことが大切になります。
そうすると、反復試行の確率という高校一年の内容と、数学Bの二項分布が、確率変数の独立という観点からつながります。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。