運動方程式 -立て方|個々の物体に働く力で文字式が圧倒的な活躍
" 運動方程式 – 立て方 “について、高校の物理基礎で扱われる内容を解説しています。
個々の物体に働いている力を把握し、物理的に等しいと考えられる関係に注目します。
ma = F という式について説明した後、具体的な練習問題を使って運動方程式の立て方について説明をしています。
数字や文字式を使い、数学の計算法則から等しい書き換えをすることもありますし、物理の考え方から等式としたりすることもあります。
物理と数学のそれぞれの法則をうまく使いながら議論を進めることが大切になるかと思います。
運動方程式 : ma=Fという式について
力 F、質量 m、加速度 a について、
ma = F となる。
この内容について、簡単な例を使って説明します。
球を右に向かって、力 F で押すということを考えてみてください。
この球の質量が m です。
右に向かって動くということは、物体が移動するので加速度が発生します。
この加速度を a としたときに、
ma = F という関係の式が成立するということにイギリスのニュートンが気づきました。
そして、物理の基本となる法則として、高校の授業で学習します。
厳密なことを述べると、加速度 a と力 F はベクトルなので、向きも考慮にいれます。
どちら向きを正の向きとするのかということを考え、逆向きを負の符号をつけて考えたりもします。
あまり複雑な内容を述べると学習し始めにハードルが上がるので、この記事では、できるだけシンプルな内容にとどめて解説をするようにしています。
F = ma という式から、数学で学習した内容も使えます。
物体の質量 m が一定の定数の場合、
a = F÷m という関係から、
力 F が大きくなるほど加速度 a の値も大きくなるということになります。
※ 分母の m が一定なので、分子の F の値が大きいほど分数の値が大きいという数学の内容を使いました。
常識的に考えるとより大きな力で球を押すと、勢いよく加速度が上がって転がるということです。
このように、物理の法則から運動方程式を作れると、数学の考察と合わせて議論を進展させることもできるので、運動方程式は、とても基本となります。
ここまで、敢えてふせていましたが、単位についても述べておきます。
ニュートンという力の単位
ma = F には、質量 m [kg] の物体に力 F [N]を加えたときに発生する加速度 a [m/s2] という単位が使われています。
左辺を見ると ma なので、単位どうしの積となり、
kgm/s2 が左辺の式の単位となっています。
右辺の F は中学の理科で学習した ニュートン N が単位です。
左辺と右辺が等しいという式なので、
kgm/s2 を N という単位と同じと思って高校の物理基礎の学習を進めることになります。
具体的な数字を使うときには、単位のことも考えて計算をするので学習の始めに単位をしっかりと押さえた上で練習を積むと良いかと思います。
以前に投稿したアルキメデスの原理という記事では、浮力という中学で学習する力について、ニュートン N についても言及しています。
それでは、ここから具体的な練習問題を使って運動方程式を立てることについて解説をします。
次の練習問題は単位の書き換えは気にせず文字を使って気楽に計算できるようにしています。
運動方程式 : 立て方
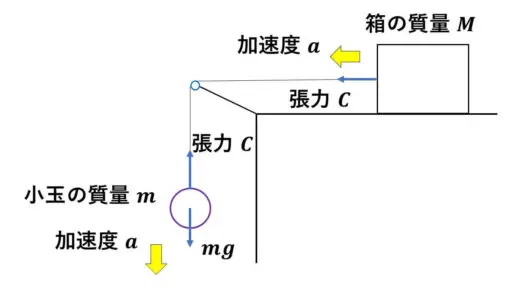
摩擦の無いなめらかな平面上に質量 M の箱があったとします。
この箱は定滑車を通して糸で質量 m の小玉につながっていて、今、下向きに小玉の加速度が a が発生しています。
※ 糸は水平面に対して平行であるとします。
重力加速度を g とし、糸の張力 C を M, m, a, g を用いて表してください。
<解答と解説>
運動方程式を立てるときに、個々の物体に働く力を考えます。
まず質量 M の箱について、運動方程式を考えます。
小玉が重力によって下向きに加速度 a ということなので、箱が糸で引っ張られることで発生する加速度も a です。
この糸が箱を引っ張る力が張力 C です。
箱の質量は M なので、運動方程式を立てることができます。
Ma = C … ① です。
これで C についての等式ができたのですが、M, m, a, g を用いて表すということから、さらに議論を進めます。
重力についても考える
重力によって小玉は下向きに落下します。
このときに、重力加速度が g です。
これは、重力に関連して発生した加速度です。
そのため、mg という質量と重力加速度の積の分の力が下向きに加えられていることになります。
そのため、質量 m の小玉についても運動方程式を立てることができます。
ただし、このときに小玉に働いている力をよく見てください。
糸でつながれていて、糸の張力によって上向きにも引っ張られています。
真逆の向きの下へは重力によって引っ張られています。
下向きに加速度 a が発生していることから、小玉に働いている力は下向きの力で、張力 C の分だけ力が減っています。
つまり、
ma = mg-C …② です。
小玉について加速度 a が発生したことについての運動方程式の力は、重力によって下向きに引かれる力から張力 C の分だけを減らしたものになっています。
上の図のように、小玉に働いている力をきっちりと押さえておくことが大切になります。
重力による下向きの力 mg と上向きに糸が小玉を引く張力 C ですが、向きが反対になっているため、加速度 a が発生したときの運動方程式②の右辺に注意です。
この②の等式を考えるときには、まさに物理的な考え方が効きました。
それでは、糸の張力 C を M, m, a, g を用いて表します。
ここで、数学の計算を使って新しい等式をつくります。
数学の計算も使用
Ma = C … ①
ma = mg-C …②
C を 表したいので、
①-②を計算します。
(M-m)a = -mg+2C です。
そのため、
2C-mg = (M-m)a より、
2C = (M-m)a+mg です。
したがって、
C = {(M-m)a+mg}÷2 となります。
これで、C を M, m, a, g を用いて表すことができました。
ただ、他にも表し方はあります。
数学では、途中の計算がちがうけれども、同じ内容になるということがあります。
こういうときに、他の式も得られるときがあります。
他の表し方について
Ma = C … ①
ma = mg-C …②
今度は異なる計算のアプローチをしてみます。
①+②で、いったん C を消去しておきます。
(M+m)a = mg となります。
a について解くと、
a = mg÷(M+m)
= mg/(M+m) …③
③を①に代入すると、
C = Ma
= M×mg/(M+m)
= Mmg/(M+m) です。
すなわち、
C = Mmg/(M+m) です。
先ほどの計算では、
C = {(M-m)a+mg}÷2 でした。
見た目の文字式は異なるように見えますが、どちらも同じ C ということになります。
今回の記事では、文字だけを使って、計算を進めましたが、実際に数字を使った問題では計算の進め方によって計算のしやすさが異なるので、やりやすい計算手順を考えた上で計算を進めるということも大切になります。
日頃から物理の練習問題を解くときに、計算を進める先を見た練習もしておくと良いかと思います。
物理基礎の内容について述べましたが、高校の理科について化学の内容についても投稿しています。
■ 原子量-分子量
理系の方の場合は、物理の内容が数学3Cでも出題されるかもしれません。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。