ウェダーバーンの小定理 斜体 | 位数有限だと可換であることの証明

2022年10月25日

" ウェダーバーンの小定理 “は、斜体 （可除環）が有限位数であるときに可換体であるということです。

有限群についての学習のはじめの方で出てきたり、情報系の分野で出てきたりと有名な定理です。

目立つのが、群論入門でよく扱われる類等式と、高校の数学の複素数平面の単元で学習する円分多項式です。

有限位数の斜体が可換体であることの証明の理解に困っている方のお役に立てれば幸いです。

このブログ記事では、零環を斜体としないと定義して議論を進めています。

環が加法についての零元 0 とは異なる乗法単位元 1 をもち、結合律が成立しているということを前提としています。

このような環について、零元と異なる任意の元が乗法逆元をもつときに、斜体（可除環）とします。

斜体が乗法について可換であるとき、その斜体のことを可換体とします。加法についての零元とは異なる乗法単位元ということを前提として考えているので、標数 1 は定義しないという設定で、以下の議論を進めています。

ウェダーバーンの小定理を証明しようとするときに、整数で割り切れるかどうかということを判断することが多いです。

そのときの根拠となってくる内容について、大学の 2 年くらいで学習する群論の入門的な知識をしばしば使います。

このブログ記事では、有限集合 S に含まれている元（要素）の個数を位数とよび、| S | と表すことにします。

ウェダーバーンの小定理 斜体 :必要な知識の準備

ラグランジュの定理は、使いやすくて、しかも役に立ちます。

「有限群 G と、その任意の部分群 H について、| H | は | G | の約数」ということが成立します。

| G | ÷ | H | = | G | / | H | が整数（自然数）であるという根拠にできます。

さらに、ウェダーバーンの小定理を証明するとき使う類等式について説明をします。

群論入門の知識

群 G が与えられたときに、G から G への作用として、共役作用を定義することができます。

(g, x) ∈ G × G に対して、
gxg^-1 ∈ G を対応させるのが共役作用です。

この g による作用で、x は gxg^-1 へと移されることになります。

x がこの作用で動いていないとすると、
gx = xg となります。

このため、g と x が群 G の積について可換であるということと、g の共役作用で x が動かないということが同値になります。
　
今は、x が g とだけ可換ということでしたが、G の中には、単位元があるので、任意の G の元と可換な元が少なくとも 1 つは存在します。

{x ∈ G | gx = xg (∀g ∈ G)} を G の中心といいます。Z(G) と表すことにします。

この G の任意の元と可換な G の元全体は、G の部分群となります。G がアーベル群（可換群）のときには、Z(G) は G に一致します。

Z(G) は、G から G への共役作用について、共役作用で動かない元をすべて集めたものという見方ができます。

また、G が有限群のときには、ラグランジュの定理から、| Z(G) | は | G | の約数となります。

また、u ∈ G に対して、
{g ∈ G | gu = ug} は、u と可換な G の元をすべて集めたものです。

これも G の部分群となっています。u の固定部分群といわれます。G_u と表すことにします。

ラグランジュの定理から、| G_u | は | G | の約数となっています。

以下で、 G を有限群として、類等式を使います。

【類等式】

|Z(G)| + Σ (|G|÷|G_u(i)|)= |G|

ここで、各 i について、
|G| ÷ |G_u(i)| = |O_i| となっています。

次に、高校数学の複素数平面で学習した内容を発展させた内容についてです。斜体についての主定理を証明するときに使う定理を紹介します。

1のn乗根について

多項式 xⁿ － 1 に代入すると 0 になる複素数を 1 の n 乗根といいます。

そして、その数自身は 1 でなく、n 乗したときに初めて 1 となる数を 1 の原始 n 乗根といいます。

1 の原始 n 乗根の 1 つは、ド・モアブルの定理から、極形式を使って、
cos (2π/n) + i sin (2π/n)
= _nt と表されます。

この複素数 _nt に対応する複素数平面上の点は、原点を中心とする半径 1 の円周上にあります。

偏角が 2π を n 等分したものなので、n 乗すると円周上をまわって 偏角 0 = 2π となります。

そのため、 _nt が原始 n 乗根となっています。

_nt¹, _nt², … , _nt^n-1, _ntⁿ = 1 は相異なる n 個の複素数で、n 乗すると 1 となることから、
xⁿ － 1 のすべての複素数根です。

自然数 n と指数の自然数 k の最大公約数が 1 のときに、_nt^k は 1 の原始 n 乗根となります。

※ このブログ記事では、以後、二つの自然数 a と b の最大公約数のことを gcd(a, b) と表すことにします。

_nt^k の偏角は 2π × k/n なので、それ自身は 1 ではなく、gcd(k, n) = 1 ということから、n 乗したときに初めて 1 となるわけです。

1 以上 n 以下の n の約数 m について、m についての円分多項式 f_m(x) というものを考えます。

この円分多項式たちの積として xⁿ － 1 を表すことができるという次の定理も、ウェダーバーンの小定理を証明するときに使います。

【円分多項式の定理】

自然数 m についての円分多項式を
f_m(x) = Π (x – _mt^k) とする。

ここで、1 ≦ k ≦ m で、
gcd(k, m) = 1 という条件を満たして k が動く。

このとき、任意の自然数 m に対して、
xⁿ – 1 = Π f_m(x)
（m | n を満たす m が走る）

各 m について、gcd(k, m) = 1 ということから、_mt^k は 1 の原始 m 乗根となっています。

1 以上 n 以下の範囲にある n の約数が、
m₁, … , m_r のとき、m₁ についての円分多項式から m_r についての円分多項式までを全て掛け合わせると、xⁿ － 1 になるということを表している定理です。

n 個の 1 の n 乗根がすべて 1 個ずつ現れるため、xⁿ － 1 に等しくなっています。

そのため、この定理の証明ができます。実は、どの円分多項式も、整数係数の多項式となっていることが分かっていて、今回の証明で使います。

※ 整数係数となっていることの証明は、リンク先のブログ記事に書いています。

では、類等式と円分多項式の定理を利用して、ウェダーバーンの小定理を証明しにいきます。

証明の前に、斜体の位数が有限だと、どのような状態になっているのかを確認しておきます。

ウェダーバーンの小定理 :証明

H を位数が有限な斜体とします。そして、0_H を加法的単位元（零元）とし、1_H を乗法的単位元とします（ただし、0_H ≠ 1_H です）。

{g ∈ H | gh = hg (∀h ∈ H)} を Z(H) と表し、斜体 H の中心ということにします。Z(H) の中に、0_H と 1_H が含まれていることが分かります。

さらに考察を進めると、Z(H) は可換体となっています。そのため、Z(H) = H ということが示せれば、有限位数の斜体 H が可換体であることを示したことになります。

今、H が有限集合なので、Z(H) ⊂ H だから、Z(H) も有限集合です。そのため、Z(H) は有限体ということになります。

有限体については、「標数が、ある素数 p で、位数が p のベキ乗となっている」ということが証明されています。※この詳しい証明は、リンク先のブログ記事で解説をしています。

このため、
| Z(H) | = p^k (p は素数で k は自然数) と置くことができます。

Z(H) は可換体なので、ベクトル空間にスカラー作用をさせることを考えます。

Z(H) × H の元 (g, h) に対して、gh という H における乗法の積を対応させることで、Z(H) から H への作用が定義できます。

この作用と、H の加法について、H は 可換体 Z(H) 上のベクトル空間となります。

このベクトル空間 H が有限集合なので、Zorn の補題を用いることなく、H の基底の存在が示されます。

H が有限集合なので、基底を構成するベクトルの個数は有限個です。H の次元を n と置いておきます。

H の任意の元は、基底の一次結合で一意的に表されます。この一次結合でスカラー倍の部分に使われるのが可換体 Z(H) の元です。

| Z(H) | = p^k だったので、(p^k)ⁿ = p^kn 通りの H の元が生成されることになります。

よって、| H | = p^kn

これで、H の位数も素数ベキということが示されました。そして、この素数 p は H の標数になっています。

ここで、各 u ∈ H に対して、
Z_u(H) = {g ∈ H | gu = ug} という H の部分集合を定義します。

この Z_u(H) には 0_H と 1_H が含まれていて、H の加法について、H の加法部分群となっています。

Z(H) の各元は H の乗法について、H のどの元とも可換なので、特に u ∈ H について、u とも可換です。

そのため、部分集合の定義から、
Z(H) ⊂ Z_u(H) です。

H の加法について、Z(H) は Z_u(H) の部分群になっています。

よって、先ほどと同様に、Z(H) から Z_u(H) へのスカラー倍を H の積によって定義することで、Z_u(H) は可換体 Z(H) 上の有限次元ベクトル空間となります。

Z_u(H) の次元を d(u) と置くと、
| Z(H) | = p^k の d(u) 乗が、位数 | Z_u(H) | になります。

よって、
| Z_u(H) | =(p^k)^d(u) = p^kd(u)

さらに、Z_u(H) は加法群として H の部分群なので、d(u) ≦ n となっています。そして、部分斜体にもなっています。

ここで、p^k = q と置くことにします。

すると、| H | = (p^k)ⁿ = qⁿ であり、
| Z_u(H) | = q^d(u) です。

もし、u が Z(H) に含まれていない場合だとすると、u と可換ではない H の元が存在することから、Z_u(H) は H に一致しません。

したがって、位数について、
| H/Z_u(H) | = q^n-d(u) ≧ 2

g ∈ Z_u(H) から x + Z_u(H) ∈H/Z_u(H) への作用を
g(x + Z_u(H)) = (gx) + Z_u(H) と定義します。

すると、H/Z_u(H) を斜体 Z_u(H) 上のベクトル空間（自由加群）にできます。

位数有限なので、
有限個の元からなる基底を 1 つ取れます。この基底を構成する元の個数を e と置くと、
(q^d(u))^e = | Z_u(H) I^e
= | H/Z_u(H) | = q^{n – d(u)}

※ スカラー倍の部分に配置できる Z_u(H) の元が、q^d(u) 通りだからです。斜体上の加群にも基底が存在して、基底の濃度が一定ということを使いました。

このため、ed(u) = n － d(u) となり、
n = (e + 1)d(u) だから、d(u) が n の正の約数となります。
※ ただし、Z_u(H) ≠ H という前提のもとなので、d(u) ≠ n です。

それでは、ここまでで分かったことと、定義した記号をそのまま使って、ウェダーバーンの小定理を証明します。

定理の証明

【定理】

位数が有限である斜体は、可換体である。

＜証明＞

有限位数の斜体 H の中心を Z(H) とし、
| Z(H) | = q = p^k (p は素数) とします。

H を可換体 Z(H) 上の n 次元ベクトル空間と考え、| H | = qⁿ です。

各 u ∈ H に対して、Z_u(H) も Z(H) 上のベクトル空間と考え、その次元を d(u) とすると、
| Z_u(H) | = q^d(u) でした。

ここから、H の乗法群 H* = H － {0_H} について、| H* | は | H | － 1 なので、
| H* | = qⁿ － 1

H* から H* への共役作用を考えます。

H* が可換でないと仮定して、矛盾を導きます。この仮定のもとでは、H ≠ Z(H) なので、ベクトル空間の次元について、n ≧ 2 となっています。

共役作用についての H* の軌道分解を考えたとき、2 個以上の元からなる軌道が存在するので、それらを O_i (i = 1, … , α) とし、各 O_i から元 u(i) を取ることができます。

各 u(i) ∈ H* (⊂ H) の 固定部分群 H*_u(i) は、
H*_u(i) = {g ∈ H* | gu(i) = u(i)g}
= {g ∈ H | gu(i) = u(i)g} － {0_H}
= Z_u(i)(H) － {0_H}

Z_u(i)(H) を可換体 Z(H) 上のベクトル空間と考えたときの次元を d_i と置くと、
| Z_u(i)(H) | = q^d_i だったので、
固定部分群の位数は、
| H*_u(i) | = q^d_i － 1

さらに、H* が非可換という仮定から、u(i) として、Z(H) に入っていない元を取ったので、
d_i は n の約数で d_i < n となっています。

※ 先ほどの H/Z_u(i)(H) を斜体 Z_u(i)(H) 上のベクトル空間(自由加群)と考える議論によります。

よって、類等式から、
|H*| =
|Z(H*)| + Σ_i |H*|/|H*_u(i)|

つまり、
qⁿ － 1 =
q － 1 + Σ_i (qⁿ － 1)/(q^d_i － 1)

各 i について、d_i は n の正の約数、かつ d_i ≠ n です。

ここで、x を変数とする複素係数多項式についての【円分多項式の定理】を使います。

(xⁿ － 1) ÷ (x^d_i － 1) について、約分をします。

※ 円分多項式が整数係数の多項式になっているという内容を使っています。

ゆえに、整数 f_n(q) は (qⁿ － 1) も割り切るので、類等式から、q － 1 も割り切ってしまうことになります。

そのため、f_n(q) が q － 1 の約数なので、
| f_n(q) | ≦ q － 1

f_n(x) の定数項に現れている複素数は 1 の n 乗根なので、複素数平面上で対応する点はすべて原点中心の単位円周上の点です。

複素数 β と γ について、| β － γ | は、複素数平面上における 2 点間距離です。

そして、q は素数ベキなので、対応する点は実軸上で 2 + 0i に対応する点に一致しているか、それよりも右側にあります。

そのため、今、n ≧ 2 なので、f_n(x) に現れる 1 の原始 n 乗根 _nt と q との距離 | _nt － q | は 1 よりも大きくなります。

したがって、
| f_n(x) | ≧ | _nt － q | > 1

これは、| f_n(q) | ≦ q － 1 に矛盾です。

よって、背理法から、H は可換で、可換体 Z(H) 上のベクトル空間 H の次元は 1 でなければならないということになります。【証明終了】

図で確認

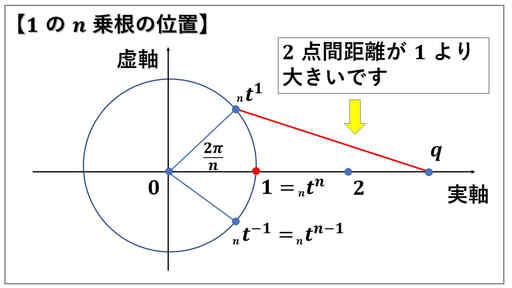
先ほどの証明の最後に使った内容です。

1 の原始 n 乗根 _nt は 1 ではなく、n 乗をしたときに初めて 1 になる複素数です。

単位円周上の点で、q = 2 だと 1 = _ntⁿ との距離が 1 となります。

しかし、1 の原始 n 乗根は 1 ではないので、たとえ q = 2 だったとしても、2 点間距離が 1 よりも大きくなります。

n についての円分多項式 f_n(x) には、
(x －_nt ) があり、
図から | q － _nt | > 1 です。

複素数 α と β について、
| αβ | = | α | | β | となることも使い、
| f_n(q) | > 1 としています。

最後の内容と関連する高校の数学の記事として、ド・モアブルの定理について解説をしています。

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。