補集合 ド・モルガンの法則【差集合の考え方も解説】
高校数学の集合の単元で、「 補集合 (complement) 」を学習します。
ベン図を見ると、すぐに理解できる感じがするかもしれません。
しかし、補集合の定義に使われている必要なパーツを、論理が見える形で確認をすることは大切です。
そうすると、差集合についても、合わせて理解できてきます。
必要なパーツが何かということを正確に押さえておくことで、他の単元への応用を円滑にできます。
敢えて細かいところまで押さえておくと良いのが、補集合です。
定義を正しく把握し、記号を適切に運用することで、理解がしやすくなり、自分の答案を作成する表現力にもなるかと思います。
まずは、記号の使い方から説明します。
全体集合 S の要素は、S の部分集合 A に含まれるか、含まれないかのいずれかになるということを表した図です。
補集合 :表記から
補集合を表す記号ですが、上にバーをつける表し方があります。
もう一つ右上に c をつける表し方もあります。
この記事では、右上に c をつけて、Ac のように、集合 A の補集合を表すことにします。
議論している大枠となる一番大きい集合を全体集合といいます。
具体的に説明していくために、今回は、全体集合 U を次のように設定します。
U = {1, 2, 3, 4, 5} を全体集合とします。
この全体集合 U の部分集合を A = {1, 2} とします。
※ 要素(元)というブログ記事で、部分集合について説明をしています。
この集合 A の全体集合 U における補集合を表す記号が、Ac です。
a∈A とすると、a は 1 か 2 のどちらかということになります。
ここで、集合 A の補集合とは、「全体集合 U の要素であり、なおかつ、A に含まれていない要素をすべて集めてできる集合」です。
そのため、U の要素 x が、A に含まれていないということは、x が A の補集合に含まれているということになります。
この例ですと、3 ∈ U は、A に含まれていない U の要素なので、Ac に含まれているということになります。
さらに理解を広げて
補集合を定義するためには、全体集合と、その部分集合を意識しておくことが必要になります。
そして、集合に要素が含まれているということと、集合に含まれていない要素ということを前もって理解しておくことも大切になります。
a ∈ A ⊂ U
集合 A と、その補集合で和集合をとると、全体集合 U となります。
ベン図を見ると明らかですが、論理的に考えると、全体集合 U の要素は、「A に含まれているか、A に含まれていないか」のどちらかに必ずなるということです。
そして、A と A の補集合の共通部分は、空集合なので、全体集合 U は、A と A の補集合に、2分割されるということになります。
※ A に含まれていて、かつ A に含まれていない U の要素が存在しないからです。
U = {1, 2, 3, 4, 5} において、
A = {1, 2},
Ac = {3, 4, 5} という状況なので、
A ∪ Ac = U となります。
和集合の理解と、共通部分の理解があると、ここまで理解を広げることができます。
補集合 ; 注釈
空集合とは、要素が 1 つもない集合のことです。
Φ (ファイ)というギリシャ文字を使って表されることが多いです。
数学では、空集合の補集合は全体集合、全体集合の補集合は空集合となっています。
ちなみに、確率の単元を学習するときには、全体集合のことを全事象といい、全体集合の部分集合のことを単に事象といいます。
そして、2 つの事象 A と B について、
A ∩ B が空集合となっているときに、A と B は互いに排反といいます。
既に学習した内容が、今後の学習の中で使われることが数学では多いです。
集合の単元は、どの単元でも、直接・間接に関わってくるので、しっかりと理解を固めておくと良いかと思います。
補集合 :ド・モルガン
補集合で集合に含まれないという否定を学習すると、その流れでド・モルガンもまとめて押さえておくと良いかと思います。
数学の論理規則で、ド・モルガン律というものがあります。
覚えやすいルールで、「かつ」や「または」の否定に関連します。
「かつ」や「または」の否定
「かつ」が否定されると「または」
「p かつ q」を否定すると、「pでない または qでない」となります。
今度は、「または」が絡む否定についてのド・モルガン律です。
「p または q」を否定すると、「pでない かつ qでない」となります。
「または」を否定すると「かつ」
「かつ」を否定すると「または」になり、「または」を否定する「かつ」になるということを押さえておくと覚えやすいです。
数学の論理規則の一つになりますので、あらゆる単元で使用されます。
ド・モルガン律
先ほどのド・モルガンと補集合に関連する集合版です。
「かつ」は共通部分、「または」は和集合です。
集合の記号では、「∩」の否定が「∪」です。
また、「∪」の否定は「∩」となります。先ほどの論理規則では、「pでない」というように書いていた部分が、集合の補集合(complement)で表されます。
【集合で表す】
(A ∩ B)c = Ac ∪ Bc,
(A ∪ B)c = Ac ∩ Bc
左辺も右辺も、どちらも同じ内容を表しているので、状況に応じて使いやすい方を使うということになります。
数学の問題文に書かれている表現は、大抵の場合は使いにくい方が書かれているときが多いのです。
ド・モルガンを使って試してみると良いかと思います。
問題文に書かれている通りで上手くいくのならそのままで。
ド・モルガンを使って書き換えた方が扱いやすい場合は、書き換えて議論を進めるということになります。
補集合の表し方ですが、右上に「c」の文字を小さくつける表記で述べてきました。
(A ∩ B)c = Ac ∪ Bc と、全体を否定したときに、「かつ」が「または」に変わり、それぞれの集合を補集合にするという表し方を論理と一緒に押さえると強力です。
ここからは、有限個の元から成る集合に含まれている要素(元)の個数を表す記号も使います。使うときに、その記号を新しく導入しますので、ご注意ください。
集合の右上に c を書く補集合の表し方を使って、有限集合どおしの和集合に含まれている要素の個数についての定理を表せます。
全体集合 U の部分集合 A について、その補集合は、Ac です。
この補集合も全体集合の部分集合となっています。
そして、A ∪ Ac = U となっていて、しかも、A ∩ Ac は空集合です。
※ 全体集合の二分割です。
全体集合 U の部分集合 A, B について、和集合や共通部分も U の部分集合になります。
補集合 :集合と差集合
補集合とよく似た定義のものに、差集合があります。
高校数学では、あまり馴染みがないかと思いますが、大学数学を学習するときには、よく出てきます。先ほどの三つの個数定理でも少し使いました。
補集合を差集合を使って表すこともできますし、一つの集合からいくつかの要素(元)を除外したいときに便利なのが差集合です。
集合 A={1, 2, 3} とします。
この集合 A から 2 という元だけを除いた集合を対象として議論をしたいときに、差集合の記号は、便利です。
「集合 A から 2 という元を除いた残りの要素を集めてできる集合」と文章で書くと長いです。
しかし、差集合(difference set)の記号を使うと、
A - {2} と端的に内容を表現できます。
※ 差集合の表記として、バックスラッシュを使うときもあります。
他の差集合の使い方として、集合 A から 集合 B に含まれている元を除くことを表現があります。
記号で表すと、A - B となります。
これは、集合 A から、集合 B との共通部分を除くということです。
差集合の具体例
A = {1, 2, 3, 4}, B = {2, 3, 6} とします。
集合 A から、集合 B に含まれている元 2 と 3 を除きます。
A - B = {1, 4}
これで、共通部分に含まれていた 2 と 3 を除くことができました。
もう少し練習してみます。
今度は、集合 B から集合 A に含まれている元を除きます。
B - A = {6} となります。
2 と 3 が除かれて、残りの6だけから成る集合 {6} となりました。慣れると使いがってが良い数学の記号です。
差集合で補集合を表す
高校数学で補集合を学習します。
全体集合が明確に指定されているときには、補集合を使って差集合 (difference set) を表すことができます。
全体集合 U の部分集合 A と部分集合 B について、「A から B に含まれている要素を除く」ということは、「A と Bに含まれていない全体集合 U の要素との共通部分」ということになります。
この内容を記号で表すと、
A ∩ Bc です。
ここで、Bc は、全体集合 U における B の補集合を表しています。
この補集合 Bc には、B に含まれていない U の元をすべて集めた集合です。
この Bc という補集合を差集合の記号で表すと、(U - B) ということになります。
つまり、集合 A に含まれている元であり、なおかつ B に含まれていない全体集合 U の元をすべて集めた集合が、A ∩ (U - B) です。
A ∩ Bc = A ∩ (U - B) と、補集合と差集合がつながりました。
さらにつきつめると、 集合 A に含まれている元です。
なおかつ B に含まれていない全体集合 U の元をすべて集めた集合ということですから、
A - B ということになります。
A ∩ Bc = A - B について、図を使ったイメージは、次のようになります。
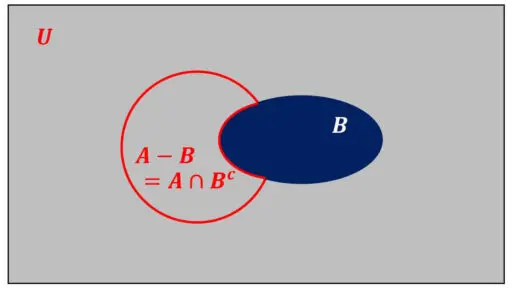
集合の記号を用いた一般的な内容を述べました。
既にしっている具体例を使って、差集合を見てみます。
U を四角形全体とします。
また、長方形全体を A とし、ひし形全体を B とします。
このときに、A-B という差集合の要素は、長方形だけれどもひし形ではない四角形ということになります。
ひし形の定義は次です。
【ひし形の定義】
4辺の長さがすべて等しい四角形をひし形という。
ブログひし形より
この定義を満たさないわけですから、ひし形でない四角形は、4つの辺の長さがすべて等しくない四角形です。
このことから、
A-B に含まれている長方形は、4つの辺の長さがすべて等しくない長方形ということになります。
例えば、縦 4cm, 横 5cm の長方形が
差集合 A-B の要素の1つです。
抽象的な集合の記号と論理ですが、よく知っている例を通して見てみると、だんだんと理解が深まるかと思います。
【論理や確率の記事】
長方形については、長方形-定義という記事で中学で学習した内容を使って高校の論理と集合について解説をしています。
差集合 (difference set) は、集合から一部の元を除くということを端的に表現でき、役に立ちます。
また、関連する記事として、反復試行の確率という記事を投稿しています。
確率の単元では、事象という集合について、全事象における余事象が補集合のことで、補集合の発想が背後で効いています。
それでは、今回のブログ記事をこれで終了します。
読んで頂き、ありがとうございました。