正十二面体 正二十面体 | 合同変換群の個数を求める【双対から群同型写像】

2023年9月3日

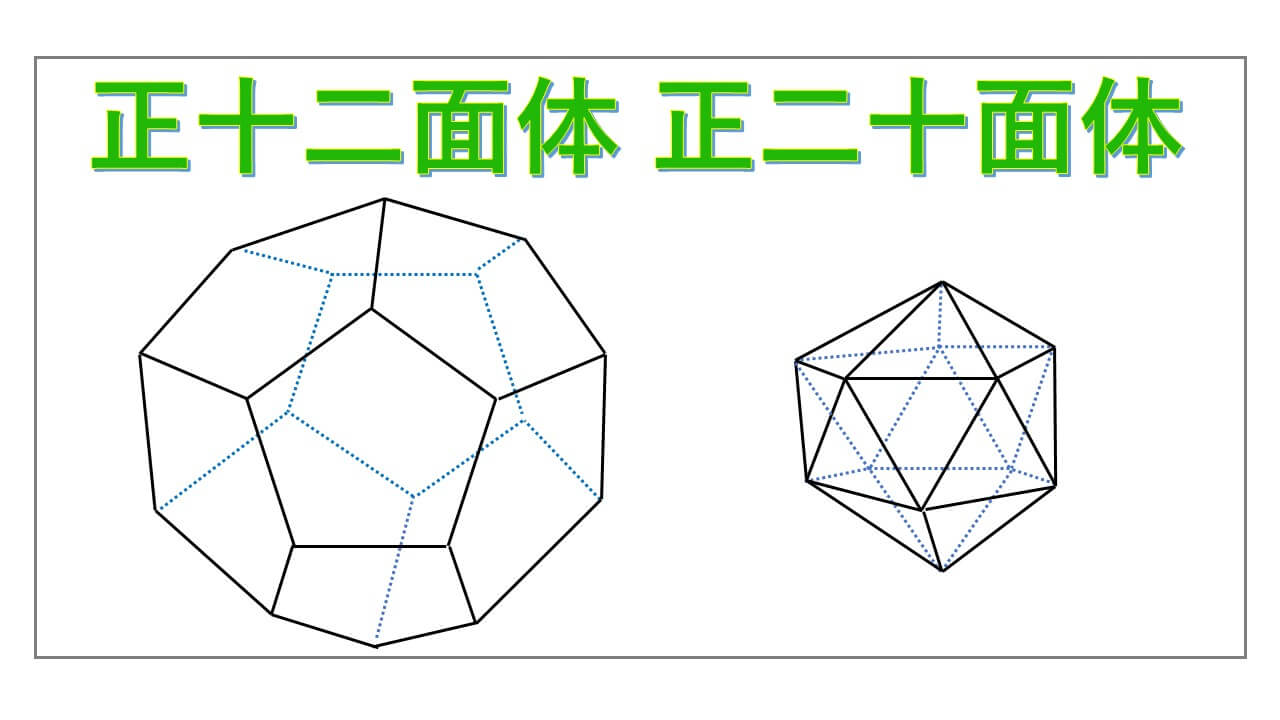
「 正十二面体 正二十面体 」のそれぞれの合同変換群の位数を求めています。

三次元のユークリッド空間において、二点間の距離を変えない変換を合同変換といいます。

正多面体をそれ自身に移す合同変換全体が、その正多面体の合同変換群です。

置換群（対称群）についての入門的な内容を使って、正十二面体の合同変換群の位数と、正二十面体の合同変換群の位数を求めます。

合同変換の積は、写像の合成で定義しています。

正十二面体 正十二面体 :置換群の発想

正十二面体を正十二面体に移す合同変換を考えます。

正十二面体を合同変換で動かすと、十二個の頂点が、置換されることになります。

そのため、正十二面体の頂点の動きに焦点を当てると、異なる 20 個の頂点の置換（入れ替え）と考えることができます。

そこで、正十二面体の合同変換を 20 個の頂点全体 Ω に制限することにより、Ω上の対称群（置換群）の部分集合と考えることができます。

ただし、十二個の面をバラバラにして入れ替えてから、つなぎ合わせるということは合同変換とは考えません。

あくまで正十二面体の回転移動のような形を変えない変換について考えています。

そのため、Ω上の置換は 20! 個ありますが、合同変換であるために、頂点の置換には制約がつきます。

また、正十二面体を全く動かさないという恒等変換も合同変換の一つと定義しています。

g, h を正十二面体の合同変換とすると、h で正十二面体をそれ自身に移してから g で再び正十二面体をそれ自身に移すと、結局は正十二面体をそれ自身に移したということになります。

そのため、正十二面体の合同変換を二つで合成写像を考えると、その合成写像も正十二面体の合同変換ということになります。

そこで、写像の合成で二項演算を定義すると、G における二項演算は結合律を満たします。

また、合同変換によって、Ω にもたらされる頂点の置換について、その逆置換で頂点を移すと、合同変換を施される前の状態に戻せます。

ということは、このもとに戻す操作で、正十二面体の形を変えずに正十二面体を正十二面体に移していることになります。

そのため、この逆置換も正十二面体の合同変換として考えます。

これで、恒等変換を単位元とし、Ωの置換群が得られました。

正十二面体の合同変換群を、Ωという 20 個の頂点から成る集合の置換群（20次対称群の部分群）とみなして、議論を進めます。

正二十面体についても、同様に 12 個の頂点の置換群（12次対称群の部分群）として考えます。

正多面体の双対

【頂点と辺の個数】

◆ 正十二面体の頂点と辺の個数は、それぞれ 20, 30 である。

◆ 正二十面体の頂点と辺の個数は、それぞれ 12, 30 である。

オイラーの多面体定理より

ここで、正十二面体と正二十面体の双対が有名です。

正十二面体は、一つの面が正五角形です。合同な正五角形 12 個から 12 個の面を持っています。

これらの正五角形の重心を、線で結びます。すると、正十二面体に、12 個の頂点から成る空間図形が内接していることになります。

そして、その内接している多角形の辺の長さは、どれも同じ長さになっています。

1 つの重心から、5 本の線を引いたので、
5 × 12 = 60 です。

しかし、この計算だと、同じ線を 2 回数えているので、2 で割ります。

(5 × 12) ÷ 2 = 30 が、正十二面体に内接している空間図形の辺の個数です。

頂点が 12 個で、辺が 30 本あり、どの辺も同じ長さなので、内接している空間図形は、正二十面体ということになります。

同様に、正二十面体のそれぞれの面である正三角形の重心たちを線で結びます。

20 個の頂点で同じ長さの辺から成る空間図形が内接しています。

1 つの重心から 3 本の線分を引いています。重複も考慮すると、同じく辺の本数が求まります。

辺の個数は、
(20 × 3) ÷ 2 = 30 です。

20 個の頂点で、辺の本数 30 で、どの辺も同じ長さの空間図形が内接しています。この空間図形は、正十二面体です。

以上の内容をまとめます。

◆ 正十二面体には、正二十面体が内接

◆ 正二十面体には、正十二面体が内接

ここから、置換を考えるときに、よく使う手を使います。

正十二面体 正二十面体 :誘導される置換

ここで、正十二面体の合同変換群（正十二面体群）に含まれる元の個数（位数）を求めることを考えます。

そのために、正二十面体の合同変換群（正二十面体群）との関係を考えます。

正十二面体を合同変換で動かすと、内接している正二十面体も動かすことになります。（ただし、恒等変換では動かさないという置換がなされています。）

すると、正十二面体の合同変換は、内接する正二十面体の 12 個の頂点を置換することになります。

そのため、正十二面体の 20 個の頂点全体Ω を表す置換は、内接する正二十面体の 12 個の頂点全体から成る集合の置換となります。

そのため、正十二面体の合同変換を20次対称群の置換と考えていたわけですが、その置換から、12 個の頂点の置換が得られることになります。

そのため、正十二面体の合同変換群は、正二十面体の合同変換群に埋め込まれます。

逆に、正二十面体の合同変換群は、内接する正十二面体の合同変換群に埋め込まれます。

どちらも 20次や 12次の対称群の部分群だったので、有限群です。

ここまでの内容を群準同型写像の記号を使って整理します。

正十二面体の合同変換群を G とし、正二十面体の合同変換群を H とし、G から H への埋め込みを φ, H から G への埋め込みを Ψ と表すことにします。

G ≅ φ(G) ⊂ H なので、
|G| = |φ(G)| ≦ |H| … (1)

一方、H ≅ Ψ(H) ⊂ G なので、
|H| = |Ψ(H)| ≦ |G| … (2)

(1), (2) より、
|G| = |H| となっています。

すなわち、
|φ(G)| = |G| = |H| なので、
φ は全射になっています。

よって、φ(G) = H となり、
G と H は群同型ということになります。

同型なので、特に位数が同じなので、正十二面体の合同変換群（正十二面体群）の位数と正十二面体の合同変換群（正二十面体群）の位数が同じになっています。

有限群の位数のように、群同型写像で保存される性質については、扱いやすい方で議論して調べることができます。

今回の記事では、正十二面体群の位数を求めるために、正二十面体群の位数を求めることにします。

十二個の頂点の置換を考える

正二十面体の合同変換で、十二個の頂点が置換されます。

まず、この正二十面体群の置換が、十二個の頂点の頂点から、どの二つの頂点を取ってきても、置換で移り合うことを示します。

a₁, … , a₁₂ を正二十面体の頂点とし、これら 12 個の頂点全体から成る集合を X とします。

a_i は恒等置換で a_i に移ると考えるため、
異なる頂点が、移り合うことを示します。

正二十面体群を H とし、
{h(a₁) | h∈H} という軌道を考えます。

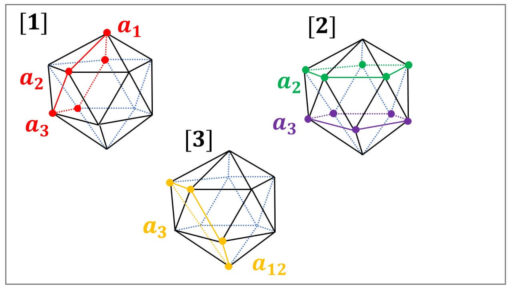
[1] で、赤色の正五角形を重心を中心に 72°回転させるという合同変換を f∈H とします。

f と f の合成を f²∈H です。

a₂ = f(a₁)∈{h(a₁) | h∈H},
a₃ = f²(a₁)∈{h(a₁) | h∈H} です。

[2] で、緑色の正五角形の中心角 72°の回転を s, 紫色の正五角形の中心角 72°の回転を t とします。

sⁱ, t^j (1, j = 1, … , 5) は H の元です。

sⁱf, t^jf という合成も H の元です。

そのため、
sⁱ(a₂) = (sⁱf)(a₁),
t^j(a₃) = (t^jf)(a₁) は、
{h(a₁) | h∈H} に含まれています。

つまり、{h(a₁) | h∈H} に緑色や紫色の頂点が、全て含まれることになります。

最後に、[3] で、オレンジ色の正五角形の中心角 72°の回転を k とします。

kf²∈H です。

そのため、
a₁₂ = k(a₃) = (kf²)(a₁) は、
{h(a₁) | h∈H} に含まれています。

これで、{h(a₁) | h∈H} に十二個の頂点が全て含まれることが分かりました。

逆置換も合わせると、
{h(a₁) | h∈H} に含まれている任意の二点は、合同変換による置換で移り合うということになります。

{h(a₁) | h∈H} = X というように、群の置換作用を受ける集合の任意の二点が移り合うとき、群の置換作用が推移的であるといいます。

transitive とこのことを英語で言います。

ここで、作用について、軌道に含まれている元の個数についての性質を使います。

一つの軌道内の元の個数

【定理】

有限群 G が有限集合 X に（置換）作用をしているとし、X の元 a を含む軌道を O(a), a の固定部分群を G(a) とする。

このとき、
|G| = |O(a)| × |G(a)| である。

群の作用より

この G(a) という固定部分群は、a を動かさない G の元たちです。

先ほどの図を用いた内容では、置換作用をする群が H で、有限集合 X の元 a₁ を含む軌道を考えました。

H の置換作用は推移的で、a₁ を含む軌道は X に一致していました。

そのため、
|O(a₁)| = |X| = 12 です。

次に、
H(a₁) = {h∈H | h(a₁) = a₁} という固定部分群の位数が分かれば、H の位数が計算で求まることになります。

h∈H(a₁) とすると、h は十二個の頂点の置換であり、かつ頂点 a₁ を動かさない置換です。

そうすると、頂点 a₁ と辺で結ばれている五個の頂点の h による像の位置が絞られます。

頂点 a₁ と辺で結ばれている正五角形の頂点を x₁, x₂, x₃, x₄, x₅ とします。

正十二面体の形を変えない合同変換ですから、
1 ≦ i ≦ 5 について、
h(x_i) は h(a₁) = a₁ と辺で結ばれていることになります。

そのため、h は、正五角形の置換と考えられます。

正五角形x₁x₂x₃x₄x₅ の隣接関係を変えることはできません。

そのため、h は、これら五個の頂点の巡回置換 σ または、そのベキ乗（逆置換であるマイナス乗も含む）となります。

つまり、
σ = (x₁, x₂, x₃, x₄, x₅),
または σ^r (r は整数) です。

σ^-1 = σ4 なので、h は、
σ⁰, σ¹, σ², σ³, σ⁴ の 5 個のいずれかになります。（σ⁰ は恒等置換のことです。）

これで、H(a₁) の位数が 5 と分かりました。

よって、
|H| = |O(a₁)| × |H(a₁)|
= 12 × 5 = 60

以上より、正二十面体群の位数が 60 と分かりました。

上述のように、正十二面体群の位数が等しかったことから、正十二面体群の位数も同じ 60 です。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。