極大部分群 | 有限生成な群の極大部分群の存在を考える

群 G の " 極大部分群 " M とは、M が G の真部分群であって、M を真に含む G の真部分群が存在しないということです。
例えば、5 次交代群は 5 次対称群の極大部分群となっています。有限群で位数が明確に分かっていて、この例だと包含関係に極大と、すぐに分かります。
気分を楽にする例を押さえておきつつ、位数が有限とは限らない有限生成な群について考えます。
全体 G が単位群という自明な場合を除いて、有限生成な群 G には、極大部分群が存在します。
この存在証明を、ツォルンの補題を使って行います。
集合論の入門内容で学習したツォルンの補題を使う練習に、群論の入門内容です。
極大部分群 :包含関係で順序を定義
有限生成な群(単位群ではない)に、極大部分群が存在することを証明するにあたって、準備となる命題を一つ示します。
群 G の部分群で、条件を満たすものをすべて集めた集合たちの集まりを T としたときに、T において集合の包含関係を用いて半順序を定義します。
この命題の証明で、ツォルンの補題を使います。
【命題】
群 G と、G の元 g が与えられたとする。そして、H を g を含まない G の部分群とする。
このとき、H を含み、g を含まない G の部分群の中で、極大なものが存在する。
<証明>
H を含み、g を含まない G の部分集合をすべて集めたものを T と置きます。
H∈T なので、T は空ではありません。
ツォルンの補題を使うために、T が帰納的であることを示します。
T から全順序となっている集合系を任意に取り、それを S とします。
このとき、S に含まれている G の部分群すべてで和集合を考えます。
K* = ∪K∈S K と置きます。
K* が G の部分群であり、H を含むが g を含まないということを示すと、K* が T に含まれていることになります。
包含関係について、K* は、S に含まれる任意の G の部分群を含んでいます。
そのため、K*∈T が示せると、
K* が S の一つの上界ということになります。
そうすると、任意に取った全順序部分集合系 S が上に有界ということで、ツォルンの補題から、極大な部分群が存在することになります。
これで、証明の方針が確定しましたので、
K*∈T ということを示します。
集合系に集合が含まれるためには
ここで、T をどのように定めていたのかを確認しておきます。
G の部分群で、H を含むが、g を含まないものを全て集めた集合系が T でした。
そこで、次の三点をチェックします。
① H を含む
② g を含まない
③ G の部分群となっている
それでは、①から確認します。
K* = ∪K∈S K でした。
和集合に現れる各 K は、
K∈S ⊂ T となっています。
そのため、各 K∈S は、H を含んでいます。
そのため、
H ⊂ ∪K∈S K = K* となっています。
これで、①が確認できました。
次に②の確認です。
各 K∈S は T の元なので、T の定め方から、K は g を含んでいません。
そのため、g∈K* = ∪K∈S K だとすると、和集合の定義から、
ある K0∈S が g を含むことになり、矛盾します。
よって、K* は g を含まないということが分かりました。
いよいよ③の確認です。K* が H を含み、g を含まないことは分かりましたが、K* が G の部分群でなければ、すべてが水泡に帰してしまいます。
③の確認が大切なわけですが、そのときに、部分群であることの判定方法を使います。
本当に部分群なのかの確認
K* = ∪K∈S K が G の部分群であることを示すと、目指していた K* が T であることを示したことになります。
ここで、部分群の判定方法を使います。
これを示すと部分群となることは、リンク先の記事で解説をしています。
x, y∈K* = ∪K∈S K を任意に選び、
xy-1∈K* であることを示すと、K* が G の部分群ということを示したことになります。
和集合の定義から、ある S の元 K1, K2 が存在し、
x∈K1, y∈K2 となっています。
S は全順序なので、
K1 ⊂ K2 か K2 ⊂ K1 です。
K1 ⊂ K2 の場合、K2 が G の部分群なので、
x, y∈K2 だから、
xy-1∈K2 ⊂ ∪K∈S K = K* です。
K2 ⊂ K1 の場合も、同様に、
xy-1∈K1 ⊂ ∪K∈S K = K* となります。
これで、K* が G の部分群であることが確認できました。
上述のように、ツォルンの補題から、
T には極大元 M が存在します。【証明完了】
この【命題】を使って、次の【定理】を証明します。極大部分群の存在を示したいのですが、より一般的なものを証明する方が証明しやすいので、まず一般化したものを証明します。
極大部分群 :より一般的な状況を証明
【定理1】
群 G は有限生成であるとし、
H を G の真部分群であるとする。
(G は単位群ではないとする。)
このとき、H を含む G の真部分群の中で、包含関係について極大な M が存在する。
<証明>
g1, … , gn をという有限個の元で G が生成されているとします。
H は G の真部分群だから、g1, … , gn の中に、H に含まれないものが少なくとも 1 つ存在します。
(g1, … , gn が、すべて H に含まれると、G を生成し、G と H が一致してしまいます。すると、H が G の真部分群であることに反します。)
g1, … , gn のうち、H に含まれないものを一つ取り、gj とします。
そして、g1, … , gn のうち、H に含まれないものの個数を a 個とします。
先ほど示した【命題】から、H を含み gj を含まない G の部分群をすべて集めると、その中に極大な K1 が存在します。
そこで、K1∪{gj} によって生成される G の部分群を H1 と置きます。
今、H1 = G または H1 ≠ G の場合が考えられます。
H1 = G の場合には、K1 が H を含む G の真部分群の中で極大なものになります。
実際、K1 を真に含む G の真部分群 L が存在したとすると、矛盾が生じます。
gj が L に含まれていないとすると、
H ⊂ K1 ⊂ L なので、K1 が H を含み gj を含まない G の部分群の中で極大であることに反します。
そのため、gj∈ L となります。
すると、K1∪{gj} ⊂ L となり、H1 の生成元がすべて L に含まれることから、
H1 ⊂ L となります。
H1 = G の場合を考えていたので、
G ⊂ L となり、L が G の真部分群であることに矛盾します。
よって、K1 を真に含む G の真部分群 L が存在しないことになり、K1 が H を含む G の真部分群の中で極大ということになります。
つまり、H1 = G の場合は、示したい結論が成立するということです。
そこで、H1 ≠ G の場合を考えます。
H1 ≠ G より、g1, … , gn の中に、H1 に含まれないものが少なくとも 1 つ存在します。
g1, … , gn の中から、H1 に含まれていないものを一つ取り、gj’ とします。
gj∈H ⊂ H1 なので、g1, … , gn のうち、H に含まれないものの個数 は、
(a-1) 個以下となっています。
【命題】より、H を含み gj’ を含まない G の部分群の中で、極大な K2 が存在します。
K2∪{gj’} によって生成される G の部分群を H2 とします。
H2 = G の場合は、先ほどと同様にして、K2 が求める極大な部分群です。
H2 ≠ G の場合は、上述のような操作を繰り返します。
つまり、Hi ≠ G のとき、
g1, … , gn の中に、Hi に含まれないものが少なくとも 1 つ存在するため、Hi に含まれない生成元 gs(i) を一つ選び、Hi∪{gs(i)} で生成される部分群を Hi+1 とします。
そして、【命題】から、
Hi+1 を含み、gs(i) を含まない極大な部分群 Ki+1 を取ることができます。
すると、g1, … , gn は有限個しかないので、有限回の操作で終了します。
つまり、3 以上の自然数 β が存在し、
i+1 = β のとき、
Hβ = G となり、Kβ が求める極大な部分群となります。【証明完了】
この【定理1】の H として、単位群 {e} とすると、有限生成な群 G には、極大部分群が存在することになります。
特に極大部分群が存在
【定理2】
群 G が有限生成であるとする。ただし、G は単位群ではないとする。
このとき、G の真部分群の中に、極大な部分群が存在する。
<証明>
単位群 {e} は G の真部分群なので、G には真部分群が少なくとも一つ存在することになります。
有限生成な G の真部分群は、部分群の定義から、どれも単位群 {e} を含みます。
よって、【定理1】より、単位群 {e} を含む真部分群の中で極大なものが存在します。【証明完了】
この【定理2】の結論で存在が示された部分群が、G の極大部分群です。
この【定理2】から、G が位数 2 以上の有限群だと、G は有限生成なので、必ず極大部分群が G の中に存在することになります。
有限な冪零群について、極大部分群に関する命題が出てきますが、その存在は、この【定理2】によって保証されています。
最後に、冪零性と極大性についての【系】を示しておきます。
極大部分群 :冪零との関連について
【系1】
群 G が冪零であり、G に極大部分群 H が存在したとする。
このとき、H は G の正規部分群である。
<証明>
G が冪零なので、G が中心列をもつことから、G の昇中心列は有限の長さで全体 G に到達します。
※ G が冪零であることと昇中心列が有限の長さで全体 G に到達することが同値になります。
{e} = Z0(G) ⊂ … Zn(G) = G を G の昇中心列とします。
ここで、
{i | 0 ≦ i ≦ n} という昇中心列に現れる項たちの添え字全体を M と置きます。
Z0(G) ⊂ H なので、i∈M で、
Zi(G) ⊂ H を満たすものが少なくとも一つ存在します。
M が有限集合なので、
Zi(G) ⊂ H を満たす添え字の中で最大のものが存在します。
それを j と置きます。
H は G の極大部分群なので、真部分群です。
そのため、j < n です。
よって、M の元について、
j < j+1 ≦ n となっています。
j の最大性から、
Zj+1(G) は H に含まれません。
j については、
Zj(G) ⊂ H です。
ゆえに、H に含まれていないある y∈Zj+1(G) が存在します。
(部分集合の定義の否定です。)
ここで、交換子群を考えます。
[H, Zj+1(G)]
⊂ [G, Zj+1(G)]
⊂ Zj(G) ⊂ H
つまり、[H, Zj+1(G)] ⊂ H です。
よって、交換子群の性質から、
H の G における正規化群を NG(H) と置くと、
Zj+1(G) ⊂ NG(H) となります。
※ 交換子群という記事で、この正規化群についての内容を証明しています。
よって、H に含まれていない y は、
y∈Zj+1(G) ⊂ NG(H) となっています。
H は部分群なので、
H ⊂ NG(H) ですが、
y∈NG(H) は H に含まれていないため、
H は NG(H) の真部分群となっています。
したがって、H が極大部分群であることから、
NG(H) = G です。
これは、H が G の正規部分群であることを示しています。【証明完了】
証明で考えた論理と集合のイメージです。
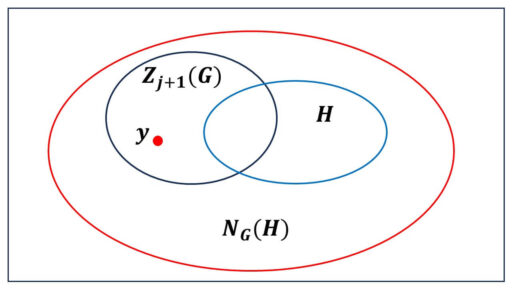
y∈Zj+1(G) は H に含まれていないけれでも、NG(H) に含まれていました。
H ⊂ NG(H) ですが、
y∈NG(H) なので、
H は NG(H) に真に含まれていることになります。
図をイメージしつつ、押さえるべきところを論理的に確定することが大切になります。
G が冪零な有限群であるときは、G の位数が 2 以上のときに、必ず極大部分群が存在します。そのため、【系1】から次の【系2】が即座に導かれます。
有限群が冪零のときに必ず成立すること
【系2】
有限群 G が冪零であるとする。ただし、G の位数は 2 以上とする。
このとき、G の極大部分群 H は正規部分群であり、H の G における指数は素数である。
<証明>
【系1】より、H は G の正規部分群です。
剰余群 G/H の位数が合成数だと仮定して矛盾を導きます。
G/H の位数が合成数だと、
シローの定理から、G/H には単位群でも G/H でもない真部分群が存在します。
その真部分群を K/H とすると、
KH は H を真に含みます。
すると、H の極大性から、
KH = G となり、
G/H = KH/H = K/H となります。
これは、K/H が G/H でないことに矛盾します。
そのため、G/H の位数は素数でなければなりません。
つまり、H の G における指数は素数です。【証明完了】
それでは、これで、今回の記事を終了します。
読んで頂き、ありがとうございました。