基底変換行列 | 基底を取り替えるときに使う遷移行列の理論の解説

2023年5月2日

" 基底変換行列 “は、線形空間の基底を取り替えることを表す行列になります。

一つの基底で、線形空間の各元を一次結合で表すことで、その元を列ベクトルを使って成分表示することができます。

他の基底でも、列ベクトルの成分表示をするとします。

このときの列ベクトルの成分の変更を基底変換行列を用いて表します。

線形写像の行列表示の理論と合わせて、基底変換行列について押さえておくと良いかと思います。

有限次元の線形空間についての線形写像の対応を、列ベクトルに行列を掛けることで表します。

体 K の元を成分とする m 行 1 列の m 次列ベクトル全体を K^m と表すことにします。

K^m は K 上の m 次元線形空間となっています。

基底変換行列 :線形写像を行列で

V を体 K 上の m 次元ベクトル空間とし、W を体 K 上の n 次元ベクトル空間とします。

{v₁, … , v_m} を V の基底とし、
{w₁, … , w_n} を W の基底とします。

そして、f : V → W を、V から W への線形写像とします。

この f を行列の乗法を用いて表すことを考えます。

x ∈ V を任意にとってきたときに、x を V の基底の一次結合で表しておきます。

そして、v₁ から v_m のそれぞれについて、f による対応先である f(v₁) から f(v_n) を、W の基底の一次結合でも表しておきます。

x = Σ_j x_jv_j と、x を v₁から v_m の一次結合で表しました。j は 1 から m までの自然数を動きます。

※ この一次結合によって、x と m 次列ベクトル (x_j) が対応しています。(x_j) は j 行 1 列の成分が x_j となっている列ベクトルのことです。

各 j (j = 1, … , m) について、
f(v_j) = Σ_i k_ijw_i とします。

ここで、i は 1 から n まで動きます。W における基底の一次結合で f(v_j) を表しました。

つまり、V の基底を構成している各ベクトルの f による像を、W における基底の一次結合で表しています。

Kⁿ において、(k_ij) という n 行 1 列の列ベクトルが、f(v_j) に対応しています。

※ (k_ij) は i 行 1 列の成分が k_ij となっている列ベクトルです。

ここまでの内容から、x ∈ V の f による像を、W における基底の一次結合で表せます。

f(x) = Σ_j x_jf(v_j)
= Σ_j x_j(Σ_i k_ijw_i) = Σ_i (Σ_j k_ijx_j)w_i

f は線形写像なので、f(x) は、f(v₁) から f(v_n) の一次結合となりますが、この各 f(j) を W の基底の一次結合で表しておきます。

f(x) に対応する列ベクトルは、
(Σ_j k_ijx_j) です。

これの i 行 1 列の成分が、
Σ_j k_ijx_j となっています。

こうすることで、x に対応する列ベクトルと、f(x) に対応する列ベクトルを基底の一次結合に現れたスカラー倍たちで作れます。

では、線形写像 f を行列の乗法を使って表します。

fを表す行列

x ∈ V と (x_j) ∈ K^m が対応し、
f(x) ∈ W と (Σ_j k_ijx_j) ∈ Kⁿ が対応しています。

A = (kij) と置きます。A は n 行 m 列の行列となっています。
（1 ≦ i ≦ n, 1 ≦ j ≦ m）

ここで、(x_j) ∈ K^m に左から行列 A を掛けると、
(Σ_j k_ijx_j) ∈ Kⁿ となります。

つまり、
A(x_j) = (Σ_j k_ijx_j)

左から A を掛けるということが、
K^m から Kⁿ への線形写像となっています。

(x_j) → (Σ_j k_ijx_j) が、f : V → W に対応する線形写像です。

ここまでの内容は、有限階数の自由加群についても成立します。

その際は、体 K を環 R として、同じ議論をすることで、加群準同型写像の行列表示になります。

線形写像の行列表示に、さらに基底変換の内容を加味することもあります。

ここからは、基底を取り替えることについて説明します。

基底変換行列 :基底を取り替える

体 K 上の m 次元ベクトル空間の基底を
{b₁, … , b_m} とします。

先ほどは、{v₁, … , v_m} を V の基底としていました。

ここで、{b₁, … , b_m} を基底として、線形写像 f を行列表示するよりも、
{v₁, … , v_m} を V の基底として f を行列表示した方が、何らかの都合が良かったとします。

この基底を取り替えるということは、K^m から K^m への線形変換を引き起こします。

次で、このことを説明します。

列ベクトルの成分の変更

体 K 上の m 次元ベクトル空間 V の基底を
{b₁, … , b_m} とします。

f : V → W という線形写像を、この基底ではなく、はじめに述べた {v₁, … , v_m} を使って行列表示をすることを考えます。

このときに、基底の取り替えをします。

x ∈ V が、
x = Σ_i s_ib_i … (1) と、
{b₁, … , b_m} の一次結合で表されていたとします。

先ほどは、
x = Σ_j x_jv_j … (2) と、
{v₁, … , v_m} の一次結合で表されていました。

このとき、K^m から K^m へ、次のようにして、線形変換が引き起こされます。

x に (s_i) ∈ K^m という m 行 1 列の列ベクトルが対応しています。

(1) の一次結合に使ったスカラー倍の部分が、列ベクトルの各成分として使われています。

一方、(2) から、
x に (x_j) ∈ K^m という m 行 1 列の列ベクトルが対応しています。

そのため、(s_i) → (x_j)

という K^m から K^m への対応を考えることができます。

つまり、{b₁, … , b_m} の一次結合で使ったスカラー倍を利用して作った列ベクトルに、
{v₁, … , v_m} の一次結合を利用して作った列ベクトルを対応させるということです。

この K^m から K^m への写像を φ とすると、φ は線形変換の定義を満たします。

実際、k ∈ K とすると、
kx =k(Σ_i s_ib_i) = Σ_i (ks_i)b_i

また、{v₁, … , v_m} の一次結合についても、
kx = k(Σ_j x_jv_j)
= Σ_j (kx_j)v_j

よって、φ の定義から、
φ((ks_i)) = (kx_j)

列ベクトルの各行が一斉に k 倍されているので、スカラー倍 k を外に出すと、
(kx_j) = k(x_j) = kφ(s_i)

そのため、
φ((ks_i)) = kφ(s_i)

確かにスカラー倍を保存しています。

y = Σ_i t_ib_i = Σ_j y_jv_j となっているときに、
φ(s_i + t_i) = φ(s_i) + φ(t_i) も同様にして確かめられます。

逆に、{v₁, … , v_m} から
{b₁, … , b_m} へと基底を取り替えると、φ の逆対応になっています。

つまり、φ には逆写像が存在するということになります。

線形写像（変換）の逆写像も線形写像（変換）なので、φ を m 次正方行列 C で表すと、可逆行列ということになります。

※ 可逆行列 C なので、C の行列式は 0 でないということと同値になっています。

行列を掛けることで、φ を表しておきます。

列ベクトルの対応と行列

(s_i) → (x_j) という K^m から K^m への線形変換 φ を表す行列が C です。

よって、C(s_i) = (x_j)

m×m 行列 C と m×1 行列 (s_i) の積は、
m×1 の列ベクトルです。

この行列 C を左から掛けることによって、
基底 {b₁, … , b_m} で作られた列ベクトルを、
基底 {v₁, … , v_m} で作られた列ベクトルへと変更されます。

そうすると、f : V → W を表す先ほどの行列 A を使って、K^m から Kⁿ へと移すことができます。

f を表すのに適した基底へと変更をしておいてから、行列表示するということを、行列 C を用いて考えました。

C を左から掛けることによって、
K^m → K^m, (s_i) → (x_j)

これで、基底 {v₁, … , v_m} で作られた列ベクトルへと変更をしておき、さらに、A を左から掛けることで、K^m から Kⁿ へ移しました。

K^m → K^m, (x_j) → (Σ_j k_ijx_j)

この (Σ_j k_ijx_j) は、f(x) ∈ W に対応する列ベクトルでした。

ここまでの内容を可換図式でまとめておきます。

基底変換行列 :可換図式

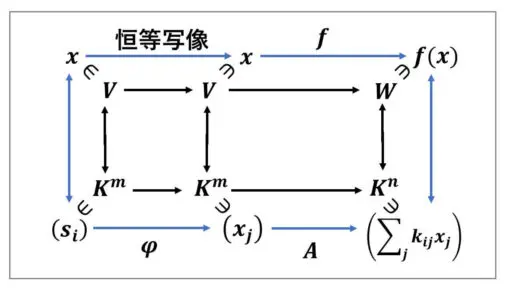
x ∈ V を列ベクトルで表示することについて、φ によって列ベクトル表示を変更しました。

先ほどの記号だと、φ を表しているのが行列 C でした。

まず、基底を取り替えたことで、
(s_i) → (x_j) と列ベクトルを変更しました。

この (s_i) に左から行列 C 乗じることで、(x_j) になります。

その後で、線形写像 f を表す行列 A を掛けます。

すると、A(x_j) = (Σ_j k_ijx_j) となりました。

この (Σ_j k_ijx_j) が f(x) に対応する列ベクトルです。

合成写像での行き先が、どの始集合の元についても等しくなる図式が可換図式です。

V → V → W という恒等写像と線形写像の合成に対応して、列ベクトルの対応が行列を左から掛けることによって表されています。

K^m → K^m → Kⁿ は、左から行列 C を掛けて、その後、さらに左から行列 A を掛けるというものです。

行列の式で表すと、
AC(s_i) = A(x_j) = (Σ_j k_ijx_j) です。

【関連する記事】

■ End(V)

■ 退化次数

ここで今回の記事を終了します。

読んで頂き、ありがとうございました。