重根 – 重解 | 形式的な多項式微分を用いて書き換える

" 重根 – 重解 “を持つかどうかについて、多項式の形式的な微分を考えるときがあります。
Fp 上の多項式についての多項式の書き換えと合わせて、よく使う方法を紹介します。
その一つの実践として、整数環上の既約多項式にも少し触れています。
それでは、よく使う性質たちを示します。
重根 – 重解 :形式的な微分などについての性質
【命題 1】
K を可換体とする。
f(x) ∈ K[x] が a ∈ K を重根にもち、
f(x) = (x - a)2g(x) (g(x) ∈ K[x]) という形であることの必要十分条件は、
f と d/dx(f(x)) = f'(x) が両方とも
(x - a) で割り切れることである。
<証明>
x = a が重根だとすると、微分すると次のようになります。
d/dx(f(x)) = f'(x)
= 2(x - a)2g(x) + (x - a)g'(x)
= (x - a){2(x - a)g(x) + g'(x)}
この右辺は (x - a) を因数にもつので、
(x - a) | f'(x)
逆に、(x - a) で f(x) と f'(x) の両方が割り切れるとすると、
f'(x) = (x - a)h(x) (h(x) ∈ K[x]) と表せます。
微分すると、
f'(x) = h(x) + (x - a)h'(x)
f'(x) が (x - a) で割り切れるという仮定から、
h(x) も (x - a) で割り切れます。
そのため、h(x) は (x - a) を因数にもつことになります。
f(x) = (x - a)h(x) だったので、
(x - a)2 はf(x) の因数です。
よって、
f(x) = (x - a)2g(x) (g(x) ∈ K[x]) という形になります。【証明完了】
次に、有限体 Fp 上の多項式について、よく使われる書き換えを証明します。
Fp上の多項式の書き換え
p を素数とし、Fp を p 個の元からなる有限体とします。
このとき、
乗法群 F×の位数が p-1 より、
x ∈ Fp を加法的零元ではない任意の元とすると、xp-1 がFp の乗法単位元になります。
そのため、xp = x
※ x が加法的零元だとしても、零元の p 乗は零元なので、
xp = x が成立します。
また、素数 p について、
自然数 r が、1 ≦ r ≦ p - 1 となっているとき、
pCr は p の倍数です。
Fp においては、p の倍数個の乗法単位元で和を取ると、加法的零元になります。
そのため、二項展開をすると、
(x + y)p = xp + yp = x + y
この内容から、次の命題が導かれます。
【命題 2】
f(x) = anxn+…+a1x1+a0 という Fp[x] 上の多項式について、
f(xp) = (f(x))p
<証明>
各 ai∈Fpに対して、
aip = ai ということを使い、f(x) の次数についての帰納法で示します。
[n = 1 のとき]
(f(x))p = (a1x+a0)p
= a1pxp+a0p
= a1xp+a0 = f(xp)
よって、n = 1 のときには、命題が成立しています。
[n ≧ 2 のとき]
n - 1 以下のすべての自然数について、命題が成立しているとして、n についての命題も成立することを示します。
g(x) = an-1xn-1+…+a1x1+a0 と置くと
f(x) = anxn+g(x)
帰納法より、
g(xp) = (g(x))p となっています。
よって、次のようになります。
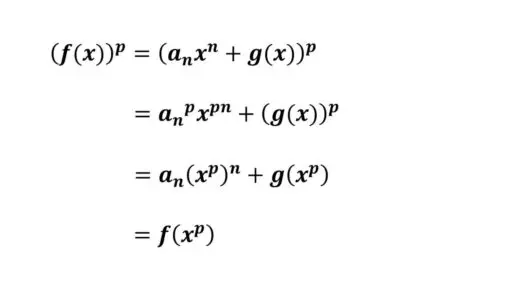
以上より、任意の自然数 n について、命題が成立していることが示せました。【証明完了】
【命題2】は、有限体 Fp 上の多項式 f(x) について、
x = xp を代入することと、f(x) を p 乗することが同じということを示しています。
Z[x]からFp[x]への環準同型
素数 p に対して、剰余環 Z/pZ は、イデアル pZ が極大イデアルであることから、可換体となっています。
位数が p で、標数も p となっています。
z ∈ Z に対して、z + pZ ∈ Z/pZ を対応させる写像は、全射な環準同型写像です。
今後、
z + pZ のことを *z と表し、
Fp = Z/pZ と置くことにします。
さらに、この環準同型写像で、
Z[x] から Fp[x] への環準同型写像を次のように定義します。
f(x) = anxn + a1x1 + a0 ∈ Z[x] に対し、
*anxn + *a1x1 + *a0 ∈ Fp[x] を対応させます。
この対応は、Z[x] から Fp[x] への環準同型写像となっています。
記号ですが、
f(x) ∈ Z[x] に対応する Fp[x] の元を *f(x) と表します。
重根 – 重解 :もう少し練習
この記事では、
多項式 h(x) の次数を
deg h(x) と表し、
h(x) と s(x) の最大公約多項式を
gcd(h(x), s(x)) と表しています。
整数 x と y の最大公約数も、
gcd(x, y) と表しています。
t を根とする Z[x] の多項式の中で、最も次数が小さい多項式を、t についての最小多項式といいます。
f(x) ∈ Z[x] が t についての最小多項式だとすると、Z 上の既約多項式となっています。
f(x) が可約だとすると、1 次以上の多項式 h1(x) と h2(x) の積として、
f(x) = h1(x)h2(x) となってしまいます。
そうすると、0 = f(t) = h1(t)h2(t) となり、Z が整域であることから、
h1(t) または h2(t) が 0 となります。
deg h1(x), deg h2(x) < deg f(x) なので、
f(x) が t を根とする最小次数の多項式であったことに矛盾。
よって、t を根とする最小多項式 f(x) は、
Z[x] における既約多項式です。
ここで、最小多項式について、よく使う命題を紹介します。
よく使う命題
【命題 3】
複素数 α ∈ C を根とする Z[x] における最小多項式を s(x) とする。
このとき、
α を根とする任意の Z[x] の多項式 h(x) は、
s(x) で割り切れる。
<証明>
もし、h(x) が s(x) を割り切らなかったとします。
h(x) を s(x) で割ったときの商を q(x) とし、余りを r(x) と表すことにします。
今、h(x) が s(x) で割り切れないので、r(x) は 0 ではありません。
剰余の定理から、
h(x) = s(x)q(x) + r(x)
0 ≦ deg r(x) < deg s(x)
両辺に α を代入すると、
0 = 0 × q(α) + r(α) = r(α)
deg r(x) < deg s(x) なので、これは、α を根とする Z[x] における最小多項式が s(x) であったことに矛盾します。
そのため、
s(x) | h(x) となります。【証明完了】
有限体という記事も投稿していまして、そこで使った命題の証明を補足として述べます。
話が変わりますが、その記事の命題1-2の証明です。
他の記事で使う証明
m∈Z について、
f(m) = m1F という元の記事の記号通りです。
「有限体 F の標数 s が 2 以上のとき、s は素数」ということを示します。
f(s) = s1F = 0F なので、
ker f の定義から、
s ∈ ker f ⊂ Z
このため、ker f は零イデアルではない整数環のイデアルです。
Z は単項イデアル整域なので、ker f に含まれる 最小の正の整数を t とすると、
ker f = tZ です。
このことから、Z/tZ と Im f が環として同型になります。
さらに、標数 s ≧ 2 なので、
f(1) = 1 1F ≠ 0 です。
そのため、1 は ker f に含まれないので、
ker f ≠ Z
t = 1 とすると、ker f = tZ = Z となってしまい、
ker f ≠ Z に矛盾します。
したがって、t ≧ 2
また、2 ≦ t < s とすると、
t = t × 1 ∈ tZ = ker f より、
t1F = f(t) = 0F となり、標数 s の最小性に矛盾します。
したがって、s = t で、
ker f = tZ = sZ
もし、s = 2 とすると、2 は素数なので、体 F の標数 s は素数だったということになります。
s ≧ 3 のときも、標数 s が合成数だとして、次のように矛盾を導きます。
t = s なので、
Z/ sZ が Im f と環として同型です。
準同型定理によって得られる環同型写像は、
φ : Z/sZ → Im f を a + sZ (a ∈ Z) に対して、
φ(a) = f(a) と定義していました。
s が合成数なので、
2 以上 s - 1 以下のある自然数 x と y が存在して、
s = xy となります。
標数 s の定義から、x と y はどちらも ker f に含まれません。
※ x ∈ ker f とすると、x1F = f(x) = 0F となり、標数 s の最小性に矛盾します。
Z/sZ において、
(x + sZ)(y + sZ)
= (xy) + sZ
= s + sZ = 0 + sZ
よって、
0(F) = f(0) = φ(0 + sZ)
= φ((x + sZ)(y + sZ))
= φ(x + sZ)φ(y + sZ)
= f(x)f(y)
x と y はどちらも ker f に含まれていませんでした。
そのため、
f(x) ≠ 0F, f(y) ≠ 0F です。
F の零元でなければ、
乗法逆元 (f(y))-1 が存在します。
これを 0(F) = f(x)f(y) の両辺に乗じると、
0F(f(y))-1 = f(x)f(y)(f(y))-1
つまり、0F = f(x)
これは、x が ker f に含まれていることを示しています。
しかし、x は ker f に含まれていなかったので、矛盾です。
よって、背理法から s は素数となります。
以上より、F の標数 s が 2 以上のとき、s は素数です。【証明完了】
ちなみに |F| < ∞ なので、F の標数が 0 でないということも示しておきます。
0でない理由
F の中には、有限個の元しかないので、
1 + 1, 1 + 1 + 1, … と続けていくと、
ある自然数 m と n について、
m < n だけれども、
m1F = n1F ということが起きてしまいます。
S = {n1F | n は正の整数} とおくと、
S ⊂ F で、F の位数が有限なことから、
S は有限集合です。
そこで、m11F, … , mk1F (ただし、各 mi は正の整数)を S に含まれるすべての元だとします。
max {m1, … , mk} = t と置き、
n = t + 1 と置くと、
n1F ∈ S なので、
mi1F = n1F となる mi が m1 から mk までの中に存在します。
mi < n なので、
0 < n - mi で、
0F = (n - mi)1F となり、
F の標数が 0 でないということになります。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。