超限帰納法 | 高校生のときに習う間接証明の一つを一般化した証明論法!
" 超限帰納法 “は、高校の数学で学習する数学的帰納法を一般化したものです。
整列集合についての命題について、適用することができます。
自然数全体は、整列集合になっています。数学の証明をするときに、高校で学習した帰納法と同じような要領で使えます。
超限帰納法を知ることで、通常の帰納法への理解もさらに深まるかと思います。
この数学の証明の論証方法を使いこなす上で、自然数 n を変数とする命題 P(n) というものを捉えておくことが大切になります。
まずは、高校の数学で学習する帰納法から説明しつつ、超限帰納法へと話を進めます。
超限帰納法 :数学的帰納法の復習から
【命題 P(n)】
自然数 n に対して、
1 + 2 + 3 + … + n = n(n + 1)/2 が成立する。
これが、自然数 n に対応する命題 P(n) です。
1 つ自然数が与えられたときに、その自然数に応じて命題が 1 つあり、その命題の真偽が数学的に確定するものを考えます。
この命題のように、命題に使われている変数 n との対応関係を認識することから、高校数学や大学数学で使われる数学的帰納法の学習のスタートです。
このような自然数についての命題が、どの自然数に対しても成立しているということを証明するときに、数学では、数学的帰納法という推論規則が認められています。
では、ここから、数学的帰納法という「どの自然数 n に対しても、命題 P(n) が成立する」ことを証明するときに適用する法則の適用手順について説明をします。
帰納法という推論規則
(数学的)帰納法を適用するときには、次の二つの内容に当てはまるかどうかを確認します。
[I] P(1) が真である。
[II] どの自然数 k に対しても、「P(k) が真ならば、P(k+1) も真」である。
[I] と [II] の両方ともが成立していることを確認しなければなりません。
片方しか確かめていないと、数学的帰納法を適用することができないので、注意です。
これについては、ドミノ倒しのイメージで、[II] だけだと、「P(k) が真ならば、P(k + 1) も真」の P(k) の部分が本当に成立しているのかが、不明ということになります。
P(k) が真かどうかは、あくまでも仮定の話です。
そこで、重要なのが、[I] になります。この [I] は仮定の話ではなく、[I] に当てはまるということは、P(1) は確かに真であるということになります。
二つの内容を組み合わせると次のようになります。
[I] より、P(1) が真ということです。さらに、[II] から、P(1) が真なので、P(2) も真ということになります。
そして、今の P(2) が真ということから、再び [II] より、P(3) も真となります。
この [II] は、エクセルVBA やプログラミングで出てくる繰り返し処理の部分になります。
もっと繰り返すと、P(3) が真なので、再び [II] より、P(4) も真となります。
5 以上の自然数についても、永遠にこのドミノ倒しが続いていきます。
自然数は無限個あり、無限なので終わりがありません。
しかし、[I] と [II] が両方とも成立しているときに、どんな自然数 n についても P(n) が成立するということにするというものです。
命題の成立に関するルールの 1 つが、数学的帰納法です。
永遠のドミノ倒しで、すべてのドミノが倒れる、すなわち、どの自然数 n についても命題 P(n) が真であるということを保証する数学的推論のルールが、数学的帰納法になります。
[I] と [II] の両方が確認され次第、「数学的帰納法より、どの自然数 n に対しても、命題 P(n) が真とすれば良い」というように考えておくと、気持ちが楽かと思います。
帰納法を適用する練習
【命題 P(n)】
自然数 n に対して、
1+2+3+…+n
= n(n+1)/2 が成立する。
※ シグマ記号を用いて表すと、
高校の数学で使うΣk=1k の公式です。
では、数学的帰納法を使って証明をします。
まず、[1] の確認です。
自然数 1 について、P(1) の左辺の値は 1 です。
P(1) の右辺の値も求めます。
1・(1 + 1) ÷ 2 = 1 なので、
P(1) の右辺の値も 1 です。
よって、直接の計算から、P(1) の左辺と右辺の値が、どちらも 1 なので、P(1) は真ということになります。
これで、[I] について確認できました。
[II] についても確認ができると、数学的帰納法という推論規則によって、どの自然数 n についても命題 P(n) が成立することが示せたことになります。
n = k (k は自然数) について、P(k) が真であると仮定します。
このとき、
1+ 2 + 3 + ・・・ + k
= k(k + 1)/2 となっています。
この等式の両辺に (k + 1) を加えても、等式が成立するので、
1 + 2 + 3 + ・・・ + k + (k + 1)
= k(k +1)/2 + (k + 1)
この右辺を通分します。
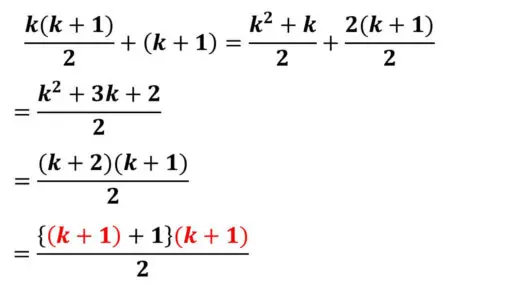
よって、
1 + 2 + … + k + (k + 1)
= {(k + 1) + 1}(k + 1)/2
先ほどの右辺に (k + 1)を加えた式から計算をしています。
通分をして、分子どおしの加法を計算してから因数分解の公式を使うと、真ん中の式と等しくなります。
n = k + 1 のときについて考えています。
そのため、敢えて赤色で真ん中に書いている式で、
n に (k + 1) を代入したことを強調するようにしています。
この式は、まさに、P(k + 1) の右辺の式です。
したがって、P(k + 1) について、確かに等式となったことを最後の行に書いています。
右辺が赤色の等式です。
これで、P(k) が真だと仮定すると、P(k + 1) も真ということが確認できたので、[II] に当てはまりました。
以上、[I] と [II] から、数学的帰納法より、どの自然数 n に対しても、命題 P(n) が成立することが示せたことになります。
[I] と [II] が両方とも成立すれば、数学的帰納法から、「どの自然数 n に対しても命題 P(n) が成立する」ということになります。
実は、帰納法には、変形版がいくつかあって、それらは、ここまで使った帰納法から、正しい証明方法として導かれます。その 1 つを後で示します。
この変形版の帰納法を使って、自然数全体が、整列集合になっているということが証明できます。
ここからは、整列集合についての内容も使って話を進めます。
超限帰納法 :大学の数学内容
ここから、大学で扱う数学の内容を説明します。
大学の数学では、様々な順序が出てくるのですが、一般に順序を ≦ の記号を使って表します。
【全順序集合の定義】
空集合ではない集合 A が ≦ について順序集合となっているとする。
このとき、任意の a, b∈A に対し、
必ず「a ≦ b または b ≦ a」のいずれかが成立するときに、A を全順序集合という。
順序集合において、二つの元 a と b について、「 a ≦ b または b ≦ a 」のどちらでもないということが起こり得ます。
しかし、全順序集合では、
「 a ≦ b または b ≦ a 」のいずれかが成立して、a と b が比較可能ということになります。
【整列集合の定義】
空集合ではない順序集合 A について、任意の空集合ではない部分集合が必ずその中に A の順序についての最小元をもつとき、A を整列集合という。
整列集合だと、必ず全順序集合になっています。それは、次のように証明できます。
順序集合 A が整列集合だとします。
このとき、任意の a, b ∈ A について、
{a, b} という A の部分集合を考えます。
{a, b} は 空集合ではないので、
最小限 min{a, b} が存在します。
min{a, b} = a のときは、a ≦ b です。
min{a, b} = b とのきは、b ≦ a です。
※ max-min というブログで、max-min の他の分野での使用について述べています。
よって、いずれの場合にも、
「a ≦ b または b ≦ a 」が成立するので、A は全順序集合となっています。
ここで、記号ですが、a ≦ b で、a ≠ b のときに、a < b と表すことにします。
超限帰納法という証明論法を導くために、整列集合についての切片を定義します。
超限帰納法という証明論法を導く
【切片の定義】
S を整列集合とする。
a ∈ S に対して、
{x ∈ S | x < a} という S の部分集合を a による S の切片といい、S<a> と表す。
この切片を利用して超限帰納法という証明論法を導きます。
高校数学の帰納法のときと同じ要領で、整列集合 S の各元 a について、a を用いた命題 P が真か偽かを議論できるときに、P を整列集合 S についての命題といいます。
【超限帰納法】
整列集合 S についての命題 P があったとする。
P について、次の【★】が示されたとすると、どの S の元についても、命題 P が成立する。
【★】
任意の a ∈ S に対して、x < a である A の各元 x について P が成立しているならば、a についても P が成立する。
<証明>
{b ∈ S | b について命題 P が成立する} という S の部分集合を A と置きます。
すると、【★】は、次の【★’】に書き換えることができます。
【★’】S<a> ⊂ A ならば a ∈ A
S = A ということが示せれば、どんな S の元についても、命題 P が成立するということになります。
そのため、S ≠ A として、背理法で示します。
もし、S ≠ A だとすると、
差集合 S - A ≠ Φ
S が整列集合なので、S - A には最小元が存在します。
そのため、a = min (S - A) と置きます。
任意の x ∈ S<a> について、x < a より、
x は min (S - A) に含まれていません。
x ∈ S - A だとすると、x < a なので、
a が S - A の部分集合であることに反します。
そのため、
x ∈ S - (S - A) = A
よって、S<a> ⊂ A となります。
すると、【★’】より、
a ∈ A となります。
a は S - A の最小元だったので、これは矛盾です。
ゆえに、背理法から、S = A となり、S のどの元に対しても P が成立するということになります。【証明完了】
超限帰納法は、a についての切片 S<a> のどの元についても命題 P が成立しているとすると、a についても命題 P が成立していることになるということが効いています。
この発想を利用して、高校数学で学習した帰納法を根拠として、有限回の操作を繰り返して、次の帰納法の変形版を示します。
帰納法の変形版
【帰納法の変形版】
自然数 n についての命題 P(n) について、次の [I] と [II] がともに成立しているとき、どんな自然数 m についても、命題 P(m) が成立する。
[I] n = 1 のときに P(1) が成立。
[II] n-1 以下のどの自然数についても命題が成立していると仮定すると、P(n) も成立。
<証明>
n = 1 のとき、P(1) が成立しています。
n = k (k ≧ 2) のときに P(k) が成立しているとして、
n = k + 1 のときにも命題 P(k + 1) が成立することを示します。
P(1) が成立しているので、[II] より、P(2) も成立します。
P(1) と P(2) が成立しているので、[II] より、P(3) も成立しています。
この議論を有限回繰り返すことで、
P(1) から P(k - 1) まで成立していることになります。
また、帰納法の仮定から、P(k) も成立しています。
よって、1 以上 k 以下のすべての自然数について、命題が成立していることになります。
そのため、[II] より、P(k + 1) も成立します。
したがって、帰納法から、
どの自然数 m についても命題 P(m) が成立していることが示せました。【証明完了】
先ほどの切片の部分を使った【★’】の部分を、有限回の操作を繰り返すということで確認しました。
ここから、自然数の性質として、任意の空集合ではない部分集合には、必ず最小元が存在するということを、変形版の帰納法で証明します。
つまり、自然数全体 N は、整列集合です。
自然数全体が整列集合ということを示せば、自然数についての命題の証明で、超限帰納法が使えるというわけです。
超限帰納法 :自然数の性質を証明
【自然数の性質】
自然数全体を N とする。
任意の空集合でない N の部分集合には、最小元(最小値)が存在する。
具体例を使って、この内容を説明します。
{99, 15, 4} ⊂ N は、空集合ではない N の部分集合です。
この部分集合の中には、その部分集合内のどの要素(元)と大小関係を比較しても最小である数が存在しています。
4 が、{99, 15, 4} の集合内の最小元(最小値)です。
このように、N のどの空ではない部分集合にも最小限が存在するというのが、自然数の性質です。
それでは、数学的帰納法を用いて、証明します。以下、空集合を表す記号として、Φ を使います。
部分集合の記号を使って
【自然数の性質】
自然数全体を N とし、
M ⊂ N を空でない部分集合とする。
このとき、M には最小元が存在する。
<証明>
M ⊂ N, M ≠ Φ とします。
1 ∈ M のとき、1 は最小の自然数なので、
1 = min M です。
N の部分集合で、n 以下の自然数を 1 つでも含めば、その部分集合が最小元をもつと仮定します。
そして、n + 1 以下のある自然数を M が含むときにも、M が最小元をもつことを示します。
M が n 以下の自然数を含んだとすると、帰納法より、M に最小元が存在することになります。
よって、M には、n 以下の自然数が 1 つも含まれていないときを考えます。
すると、n + 1 ∈ M なので、M に含まれているどの元も、n + 1 以上の自然数ということになります。
したがって、n + 1 が M の最小元となっています。
以上より、
M にどんな自然数 n が含まれていても、
M には最小元が存在することが示せました。【証明完了】
この自然数についての性質を利用して、無限降下法という証明論法も導かれます。
これで、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。