恒等式とは | 方程式との違い【関数の考え方で】

恒等式とは 「変数 x にどんな数を代入しても成立する等式」が定義と思うと早とちりになります。方程式との違いは定義を正確につかむことで理解できます。
シンプルな具体例を使って恒等式と方程式の違いを認識しておくと、高校の数学が楽になるかと思います。
実は中学で学習した関数の考え方から、恒等式というものの定義が分かります。
定義の早とちりからの主観的判断は、難し目の問題を解くときに足元をすくわれかねないので、根本からの理解が大切になります。
二つの関数が等しいということの定義を知り、そこから恒等式へと理解を広げます。
恒等式の定義に、二つの関数が等しいということが使われます。
そのために、二つの関数が等しいということの定義を先に述べます。
二つの関数が等しいことの定義の後で、恒等式の定義を説明します。
恒等式とは :定義を着実に
【関数が等しいことの定義】
定義域 S から実数全体 R への関数を f と g とする。
定義域 S のどの要素 x についても、f(x) と g(x) が必ず等しくなっているときに、関数 f と関数 g が等しいという。
中学の数学で学習した関数を使って、この関数が等しいことの定義を確認してみます。
【例】
定義域 S を自然数全体から成る集合とします。
x ∈ S に対して、一対一に対応する値を
f(x) = 2x, g(x) = 2x + 3 - 3 とします。
どんな自然数 x についても、
g(x) = 2x + 3 - 3 = 2x = f(x) となります。
3 – 3 は 0 なので、f と g で対応する値が同じになっているということです。
定義域のどの要素 x についても、f(x) と g(x) が同じ値になっているので、二つの関数 f と g は同じ関数ということになります。
関数が等しいことに慣れるために、二つの関数が異なる例も述べておきます。
関数が異なる例
定義域 S を自然数全体とします。
x ∈ S に対して、
f(x) = 2x, h(x) = 3x とします。
関数が等しいことの定義に当てはまらないことが分かります。
1 という自然数について、f(1) = 2 です。
しかし、g(1) = 3 で、f(1) ≠ g(1)
1 ∈ S について、同じ値ではないので、関数 f と関数 h は異なる関数ということになります。
ここまで、二つの関数が等しい例と、等しくない例を述べました。
実は、高校の数学で学習する恒等式とは、二つの関数が等しいということを表しています。
それでは、恒等式の正確な定義です。
恒等式の定義
定義域 S から実数全体 R への関数を f と g とする。
どの x ∈ S に対しても、f(x) と g(x) の値が必ず等しくなっているとき、関数 f と関数 g は S において恒等的に等しいという。
恒等式の定義を学習し始めたときに、「変数 x にどんな数を代入しても成立する式」と早合点してしまうと、混乱してしまいます。
変数 x といったときには、変数 x に代入する範囲を決めておかなければなりません。
この定義は、難しい問題だと突かれることがあります。関数の定義域の範囲が自然数全体であったり、実数全体と問題文に書かれていることがあります。
関数 f と g が自然数全体において恒等的に等しいという設定なのに、2/3 という有理数に対応する値が異なるなどと混乱してしまわないように注意です。
定義域が「どこか」ということを意識して恒等式に取り組むことが必要になります。
ちょっとだけ大学の数学に踏み込んで、深く二つの関数が恒等的に等しいということについて調べてみます。
恒等式とは :関数を定める式
関数とは、定義域 S の各要素に対して値をただ一つ対応させます。この関数の対応を表す式のことを定義式といいます。
文で述べると難しそうですが、中学の頃から使っている内容になります。
【例】
実数 x に対して 2x を対応させる関数を f とします。
この f は、定義域 S を実数全体とし、
各 x ∈ S に対して、2x という値を対応させる関数です。
2x という文字式によって、x に対して x を 2 倍した数を対応させるということを表しています。
ここで、注意点ですが、定義式が異なっていても、関数として恒等的に等しくなるときがあります。
この内容をシンプルな例を通して確認しておきます。
代入する範囲に注意
関数 f と関数 g の定義式が、
f(x) = 2x, g(x) = 2x2 という文字式だとします。
2x と 2x2 ですから、異なる文字式です。
しかし、定義域によっては、関数 f と関数 g が恒等的に等しいということが起こります。
f と g の定義域 S を S = {0, 1} とします。
f(0) = 2 × 0 = 0 = 2 × 02 = g(0)
ですから、f(0) = g(0)
さらに、
f(1) = 2 × 1 = 2 × 12 = g(1) なので、
f(1) = g(1) です。
よって、定義域 S = {0, 1} のどの要素 x についても、f(x) と g(x) が等しいことから、S において関数 f と g が恒等的に等しいということになります。
これが、恒等式を「変数 x にどんな数を代入しても成立する等式」と思うのは早とちりという例です。
定義式が異なっていても、定義域という代入する範囲次第で、恒等的に等しいかどうかという結果が異なるときもあり、注意です。
※ 定義域 S が実数全体だとすると、中学の数学で学習したように、f(x) = 2x と g(x) = x2 は異なる関数です。
3 という実数について、
f(3) = 6, g(3) = 18 ですから、f(3) と g(3) が異なる値です。
よって、恒等式の定義から、関数 f と関数 g は実数全体において恒等的に等しくないということになります。
定義式が異なるときは、定義域に依るということを述べました。
では、どんなときに、二つの関数が確実に恒等的に等しいと断定できるのかということが気になるところです。
単純なパターンですが、定義式が全く同じだと、二つの関数が恒等的に等しくなります。
例で確認してみます。
恒等式の例
定義域 S を実数全体とします。
定義式は、
f(x) = x2 - 1,
g(x) = (x + 1)(x - 1) だとします。
実数全体 S において、関数 f と g は恒等的に等しくなります。
理由は、
f(x) = x2 - 1 = (x + 1)(x - 1) = g(x) と定義式が同じ式だからです。
そのため、変数 x にどんな実数 a を代入しても、f(a) = a2 - 1 = (a + 1)(a - 1) = g(a) となります。
定義域である実数全体 S のどの要素 a についても f(a) と g(a) の値が等しいことから、関数 f と g は S において恒等的に等しいということになります。
式を変形して一致していることが確かめられる、つまり、同じ定義式というときには、恒等的に等しくなります。
しかし、高校の数学IIで学習する数値代入法には注意です。数値代入法で係数比較をしたときに、逆を確認することが必要になります。
これは、「定義式が異なっているけれども、その定義域においては恒等的に等しくなっている」ということが背後に絡みます。
数値代入法で、係数を決めたときに、定義式として同じかどうかは不明です。
そこで、確実に定義域のどの要素についても同じ値になっていることを示すことが、必要になります。
数値代入法については、このブログ記事の最後に解説します。
その前に、恒等式と方程式の違いについて解説をします。
恒等式とは :方程式との違い
恒等式という定義式で対応を定められた二つの関数 f と g は、その定義域の各要素について同じ値をとるということでした。
では、方程式とは何かということですが、定義式だけを見ても恒等式なのか方程式なのかは区別がつきません。
やはり、方程式とは何かということを理解しておくことが大切になります。
【方程式の定義】
着目している文字について、ある値を代入したときに左辺と右辺が一致する式を方程式という。
文章だと、難しそうに感じますが、シンプルな例を通して確認すると明確に理解ができるかと思います。
f(x) = x + 3, g(x) = 7 という定義式で、変数 x に代数する範囲である定義域は実数全体とします。
g(x) = 7 というのは、どんな実数 x に対しても 7 を対応させるという関数です。
数学IIIでは、定数関数と用語で呼ばれますが、中学で学習したグラフが横軸に平行になっている関数です。
f と g は、実数全体について、恒等的に等しくなっていません。
f(1) = 4 ですが、g(1) = 7 なので、定義域の要素 1 について、値が異なるために、恒等的に等しいことの定義に当てはまりません。
x + 3 = 7 は、x についての方程式です。
「着目している文字 x について、ある値を代入したときに左辺と右辺が一致する式」という方程式の定義をグラフで眺めてみます。
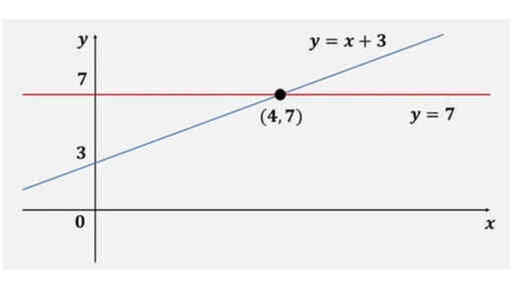
様々な実数 x に対して、左辺と右辺の定義式から定まる関数で対応する値が異なっています。
ただ、x = 4 という特別な実数に対応する値である 7 のみが、同じ値になっています。
この 4 が、「ある値を代入したときに左辺と右辺が一致する」という定義の「ある値」です。この値のことを方程式の解といいます。
グラフを用いると、内容が分かりやすくなるときもあります。
等差数列は一次関数として考えるということもでき、直線のグラフに慣れておくと、様々な単元で理解の助けになるかと思います。
今の例では、左辺と右辺が同じ値となる「ある値」が一つのみでしたが、複数あるときがあります。
たとえば、二個ある場合が、二次方程式です。
着目する文字
【練習問題】
兄が a 個のビー玉を持っています。兄の持っているビー玉の個数に 4 個のビー玉を加え、その個数を 4 倍すると、弟の持っているビー玉の個数の 2 倍となります。
弟の持っているビー玉の個数を a を用いて表してください。
弟の持っているビー玉の個数を x 個として、方程式を作ります。
2x = (a + 4) × 4
つまり、2x = 4a + 16 ・・・(2)
x と a と二つの文字があります。この a が定数です。
どんな値かは不明ですが、とにかく一定の値です。それに対して、着目している文字は x です。
「着目している文字について、ある値を代入したときに左辺と右辺が一致する式を方程式」と定義しました。
方程式の解を求めるために、後から自分で設定した文字 x と違って、a は最初から与えられていた定数になります。
(4a + 16) ÷ 4 より、x = a + 4 が、(2) に代入したときに左辺と右辺が一致する値となります。
今回の例では、着目している文字が x で、(2) は x についての方程式ということになります。
これで、恒等式と方程式について、区別をしながら解説をしてきました。
関数を定義している式が二つあって、定義域のどの要素についても二つの関数が対応させる値が等しいときに、その定義式が恒等式です。
定義式が異なっていても、定義域次第で、恒等的に等しくなるときがあります。
先ほどの内容を踏まえつつ、数値代入法で未知の係数を求めたときには、逆も確認が必要になるということについて解説をします。
これを理解するためには、必要条件と十分条件についての理解が大切になります。
恒等式とは :数値代入法について
【練習問題】
実数 a, b, c は定数です。次の等式 ★ が、どんな実数 x についても成立しています。
3x2 - 1 = a(x + 1)2 + bx + c … ★
このとき、定数 a, b, c の値を求めてください。
どんな実数 x についても、★が成立しているということは、実数全体を定義域とする関数として等しいということです。
f(x) = 3x2 - 1 という関数と、
g(x) = a(x + 1)2 + bx + c が等しいということです。
f(x) は二次関数ですから、g(x) も二次関数となっていることが分かります。
このときに、係数として関わってくる a, b, c という三つの実数を求める問題です。
ここで、数値代入法という求め方について説明をします。
どんな実数 x についても★が成立すると問題文に書いていますので、具体的な実数を x として設定します。
どんな実数についても★が成立するので、
x = 0 についても★が成立します。
よって、-1 = a + c … (1) となります。
このように、x に具体的な実数を代入して、a, b, c を使った等式を作ります。
それらを等式の性質を使って同値変形をして、a と b と c の値を決定するのが数値代入法です。
x = -1 について、
2 = -b + c … (2)
x = 1 について、
2 = 4a + b + c … (3)
(2) と (3) の左辺と右辺はどちらも同じ実数ですから、中学一年のときに学習をした等式の性質が使えます。
左辺どおしの和と、右辺どおしの和は、同じ実数です。
よって、(2) + (3) より、
4 = 4a + 2c,
つまり、2 = 2a + c … (4)
等式の性質より、(4) - (1) から、3 = a となります。
a の値が 3 と分かったので、(4) に代入をすると、2 = 6 + c となり、c = -4 と値が決まります。
c = -4 を (2) に代入すると、2 = -b -4 です。
これで、b = -6 と分かりました。
ここまでは、既に学習した通りで、スムーズに値が求まりました。
しかし、ここで疑問点が出てきます。
「数値代入法」を使って a, b, c を求めたときには、逆も成立することを確かめるように高校の数学で学習します。
なぜ、逆を確かめないといけないかという疑問について、これから解説をします。
求めたのは必要条件でした
今、数値代入法を使って、a, b, c の値を求めました。
この一連のプログラムは、次のようになっています。
★が実数全体における恒等式ならば、
a = 3, b = -6, c = -4
数学で、「p ならば q」が正しいときに、p の部分を十分条件といい、q の部分を必要条件といいます。
上で計算した数値代入法は必要条件を求めたということになります。
ここで、自然な疑問が起こります。
「a = 3, b = -6, c = -4」というのは、「x = 0, x = -1, x = 1」という限定された実数についてのときだけの話でした。
実数全体における恒等式は、どんな実数を代入しても、両辺の値が成立しなければなりません。
このことを確認しなければという疑問が残っています。
「a = 3, b = -6, c = -4」のときに、x に π(円周率)などを代入したときに、左辺と右辺が等しいのかという疑問です。
しかも、π だけではなく、実数は無限個存在します。
このように考えると、数値代入法を使ったときに、逆も成立するのかということを考えるのが必要だという感じがしてきます。
恒等的に等しいとするならば、
「a = 3, b = -6, c = -4」であるということを示しました。
よって、
結論部分の「a = 3, b = -6, c = -4」は必要条件です。
十分条件に本当になっているのかの確認をこれから行います。
十分性の確認
【逆】
a, b, c を実数とし、
a = 3, b = -6, c = -4 となっていたとします。
このとき、どんな実数 x についても次の★が成立します。
3x2 - 1 = 3(x + 1)2 - 6x - 4 … ★
実数は無限個あります。
それなら、どんな実数についても成立する計算規則を証明の根拠として考えます。
3(x+1)2 - 6x - 4
= 3(x2+2x+1) -6x -4
= 3x2+6x+3 - 6x - 4
= 3x2 - 1
すなわち、
3x2 - 1 = 3(x+1)2 - 6x - 4
これで、★が成立していることが分かりました。
今回は、二つの関数を定めている定義式は同じ多項式になっていたわけです。
定義式が同じときは、恒等式になっていました。
数値代入法で係数たちを求めると、恒等的に等しいことの必要条件を求めた状態です。
そこから十分条件にもなっていることを示さないといけないので、注意です。
恒等式の練習として、数II の内容で、
定点を通る直線という問題があります。
念のための注意ですが、大学の数学で、多項式環を学習します。
多項式環において、二つの多項式が等しいということについて、等しいということの定義があります。
複二次式というブログ記事の後半で、二変数の多項式が等しいということを解説しています。
高校数学で、難しい大学で狙われるかもしれないので、恒等式との区別に記事にしました。
今回のブログ記事で扱った内容は、多項式関数が等しいということで、関数が等しいということについて扱っています。
同じ等しいということについて、定義が異なることがあるので、学習をするときには注意です。
それでは、これで今回のブログ記事を終了します。
読んで頂き、ありがとうございました。