共通部分 和集合 ∩ ∪ | 記号の定義の把握から
共通部分 和集合 ( ∩ ∪ ) について、高校数学の学習し始めた内容から始め、難関大学の入試で問われる内容までをカバーするための根本部分を解説しています。
集合算は、大学受験では難しい大学の受験用ですが、大学数学では、とてもよく使われます。ただし、定義を押さえていけば習得は十分可能かと思われます。
根気がやや必要ですが、一つ一つの定義は習得しやすいものなので、無理なく続けていくと、そのうちに難関大学で出題されるようなものも扱えるようになってくるかと思います。
共通部分と和集合は、学習進度が進むにつれて、その重要度が増してきます。
- 場合の数や確率
- 二次不等式
- 三角関数の角の範囲
- 対数不等式…など
その他、多くの単元で、論理と合わせて集合の共通部分や和集合に関する内容が出てきます。
まさに学習の基本として、共通部分と和集合を理解が大切になります。
共通部分 和集合 :intersection と union
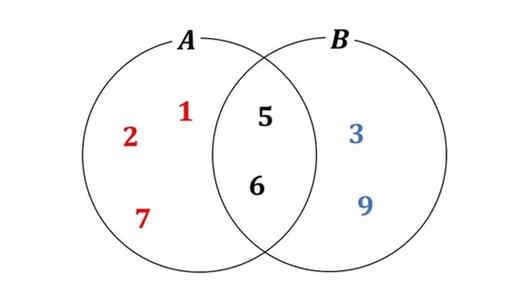
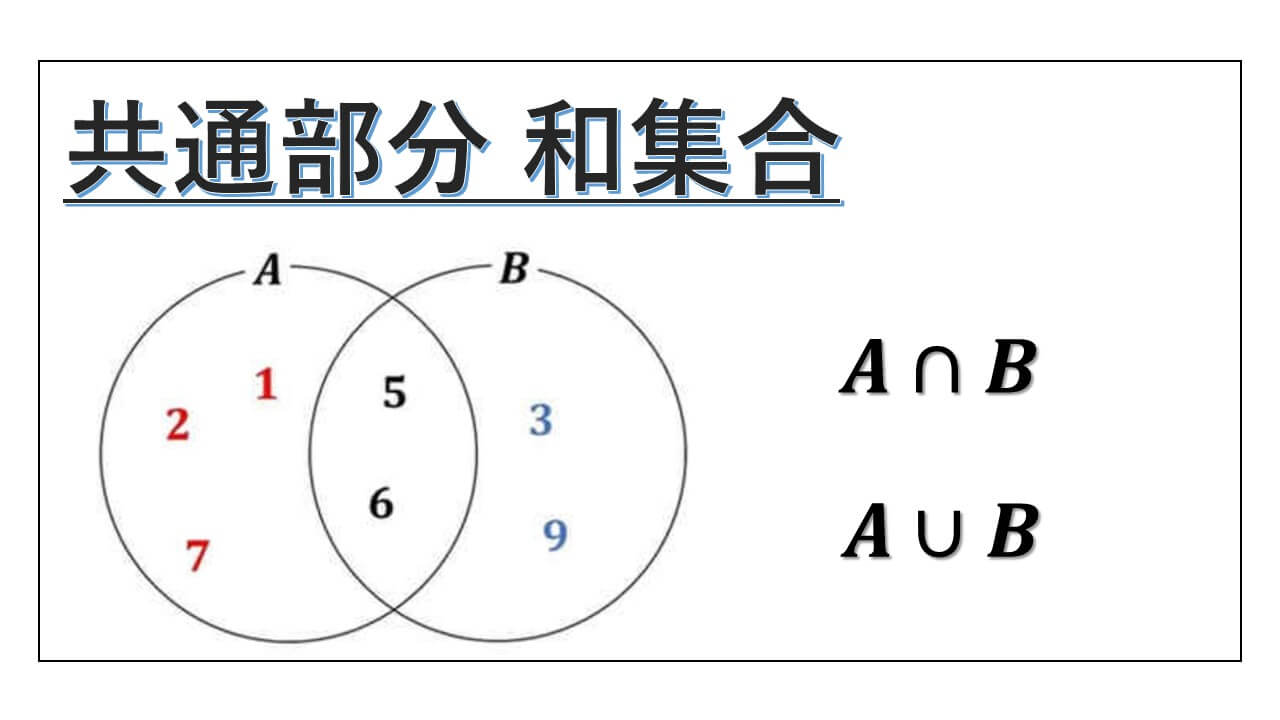
集合 A = { 1, 2, 5, 6, 7} です。
黒で書いている 5 と 6 は集合 B にも含まれています。
また、集合 B = {3, 5, 6, 9} です。
共通部分と和集合の説明
A と B のどちらにも含まれている 5 と 6 を集めた集合を考えます。
この {5, 6} という集合が、A と B の共通部分です。
A ∩ B = {5, 6}
集合 A と集合 B の和集合は、A か B の少なくとも一方に含まれている要素をすべて集めてできる集合です。
少なくとも一方に含まれているということは、次のいずれかに当てはまるということを数学では意味します。
- A に含まれ、B には含まれない
- A に含まる、B に含まれる
- A に含まれなく、B に含まれる
上の図で、 1.については、「 1 と 2 と 7」が当てはまります。
また、2.については、「5 と 6」が当てはまります。
そして、3.については、「3 と 9」が当てはまります。
これらをすべて集めた集合が、A と B の和集合、
A ∪ B = {1, 2, 3, 5, 6, 7, 9} です。
これで、和集合がどのような要素で構成されているかを明確に示すことができました。
「または」という論理も合わせて
p または q が成立するということは、p か q のうち少なくとも一方が成立するということです。
1. p が成立、q が成立しない
2. p が成立、q が成立
3. p が成立しない、q が成立
これら 3つのうち、どれか1つでも成立するということです。
したがって、A ∪ B とは、「A に含まれる」または「B に含まれる」ということになります。
共通部分と和集合は、論理の「かつ」と「または」とセットで押さえておくと、数学を学習するときに、どの単元でも出てくるので役に立ちます。
「かつ」の方は、どちらも満たすということなので、扱いやすいかと思います。
「または」は、少なくとも一方は満たすという言い方をするときがあるので、注意です。
共通部分 和集合 :練習問題
【問題】
A = {1, 3, x2 - x - 2},
B = {2, x + 1, x2 + x - 6}
A ∩ B = {0, 3} のとき、x の値を求めてください。
また、A ∪ B がどんな集合かを求めてください。
<解説と解答>
A ∩ B ⊂ A なので、A の中に 0 と 3 が含まれていることになります。
0 は 1 と異なる数なので、
x2 - x - 2 = 0 という方程式が得られます。
(x + 1)(x - 2) = 0 なので、
x = -1 または x = 2 です。
B に含まれている要素たちは、場合分けをして求めることになります。
【x = -1 のとき】
x + 1 = 0, x2 + x - 6 = 1 - 1 - 6 = -6
となっているので、B の要素が具体的に書き出せました。
B = {2, 0, -6} です。
【x = 2 のとき】
x + 1 = 3, x2 + x - 6 = 4 + 2 - 6 = 0
なので、B = {2, 3, 0}
これで、場合分けをして、B の要素をすべて求めることができました。
今度は図形を使った練習問題も考えてみます。
図形を使った論理と集合
【定義】
4つの内角が全て90°である四角形を長方形という。
ブログ長方形-定義より
【定義】
4つの辺の長さが全て等しい四角形をひし形という。
ブログひし形より
これら中学の数学で学習した内容を使って、共通部分と和集合を考えてみます。
集合 A を長方形である四角形全体とし、集合 B をひし形となっている四角形全体とします。
このとき、A∩B という共通部分が、どういった四角形となっているのかということを考えてみます。
A∩B に含まれている四角形は、長方形であり、かつ、ひし形となっています。
つまり、長方形の定義とひし形の定義を両方とも満たしていることになります。
そのため、4つの内角が全て90°で、4 つの辺の長さが全て等しい四角形ということになります。
これは、正方形です。
よって、A∩B に含まれている四角形は、正方形ということになります。
逆に、どの正方形も、長方形の定義とひし形の定義を満たしています。
そのため、A∩B に、どんな正方形も含まれることになります。
今度は、U を平行四辺形となっている四角形全体として、A と B の和集合を考えてみます。
長方形とひし形は、どちらも平行四辺形となっています。
そのため、
A ⊂ U, B ⊂ U となっています。
A または B の要素が必ず U に含まれているという状態です。
つまり、
A ∪ B ⊂ U となっています。
一般に、集合 X, Y, Z について、
X ⊂ Z かつ Y ⊂ Z のとき、
X ∪ Y ⊂ Z となります。
このように、「かつ」や「または」についての論理と合わせて集合を考えることを数学では、しばしば行います。
共通部分 和集合 :論理
共通部分と和集合について、論理と関連させて分配律を考えることがあります。
「p かつ (q または r) 」は、
「(p かつ q) または (p かつ r)」という論理規則があります。
これを集合にしたバージョンが、
A ∩ (B ∪ C)
= (A ∩ B) ∪ (A ∩ C) で、分配律が成立しています。
A ∪ (B ∩ C)
= (A ∪ B) ∩ (A ∪ C) という分配律 も成立します。
どちらも同じ集合なので、状況に応じて、使いやすい方を使えます。そのため、知っておくと役に立つかと思います。
共通部分と和集合について、大学数学で扱われる内容として、三つの集合で結合法則が成立するという集合算があります。
三つの集合で和集合をとる、もしくは三つの集合で共通部分をとるということを考えます。
このときに、結合法則が成立するので、状況に適した使い勝手が良い方を使うことができます。
不等式の範囲を考えるときに役立つ集合算について、ここから使い方を説明します。
集合算を理解する道筋
集合算について、分配法則が成立します。
【集合算】
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C),
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
※ 分配律という大学数学用のブログ記事で、証明を述べています。
はっきりとは習いませんが、これを使うことで、不等式の範囲を考察しやすくなります。数直線を用いて図から考えることもできます。
図が複雑になってきて混乱するときもあるので、論理規則から考える方法も身につけておくと良いかと思います。
不等式の範囲と集合
【論理規則】
「p かつ (q または r) 」は
「(p かつ q) または (p かつ r)」
この論理規則に基づいて、不等式の範囲を考えます。
大学受験や大学の数学に通じる内容なので、大学に入学してからも、集合論の例として不等式を復習するということもできるかと思います。
【問題】
R を実数全体から成る集合とし、次の集合たちを考えます。
A = {x∈ R | 3 ≦ x},
B = {x ∈ R | 4 ≦ x ≦ 5},
C = {x ∈ R | 7 ≦ x ≦ 9}
このとき、A ∩ (B ∪ C) を求めてください。
集合算の分配法則を使って、
A ∩ (B ∪ C)
= (A ∩ B) ∪ (A ∩ C) に書き換えて、順に集合を整理します。
A ∩ B は、3 以上の実数であり、かつ、4 以上 5 以下の範囲にあるものです。
そのため、これを集合で表すと、
A ∩ B =
{x ∈ R | 3 ≦ x ≦ 5} となります。
A ∩ C は、3 以上の実数であり、かつ 7 以上 9 以下の範囲にあるものです。
そのため、これを集合で表すと、
A ∩ C =
{x ∈ R | 7 ≦ x ≦ 9} となります。
A ∩ B または A ∩ C が求める集合なので、
A ∩ (B ∪ C)
= (A ∩ B) ∪ (A ∩ C)
{x ∈ R | 3 ≦ x ≦ 5 または 7 ≦ x ≦ 9} が求める集合となります。
集合を使わずに不等式の範囲を述べると、
「3 ≦ x ≦ 5 または 7 ≦ x ≦ 9」を満たす範囲にある実数ということになります。
最後に、例外的な記号について述べておきます。
共通部分 和集合 :空集合について
空集合 Φ が高校の数学から出てきます。
和集合や共通部分を空集合とで考えるとどうなるのかということを押さえておくと、不等式の考察に良いかと思います。
■ Φ ∪ A = A = A ∪ Φ
■ Φ ∩ B = Φ = B ∩ Φ
空集合と和集合をとっても、相方の集合のままです。
空集合と共通部分をとると、空集合になります。
この内容を知っておくと、先ほどの不等式の範囲の考察が楽になるときがあります。
例で確認
R を実数全体から成る集合とします。
A = {x∈ R | x ≦ 3},
B = {x ∈ R | 2 ≦ x ≦ 5},
C = {x ∈ R | 7 ≦ x ≦ 9}
このとき、A ∩ (B ∪ C) を求めてください。
分配律で (A ∩ B) ∪ (A ∩ C) を考えます。
A ∩ B は 2 以上 3 以下の実数なので、
A ∩ B = {x ∈ R | 2 ≦ x ≦ 3}
一方、A ∩ C は、3 以下の実数であり、
かつ 7 以上 9 以下の範囲にある実数です。
そのような実数は存在しないので、
A ∩ C は空集合 Φ です。
ここで、Φ との和集合は、相方のままだったので、
A ∩ (B ∪ C)
= (A ∩ B) ∪ (A ∩ C)
= A ∩ B ∪ Φ
= A ∩ B = {x ∈ R | 2 ≦ x ≦ 3} となります。
空集合との和集合を利用することで、考える集合を減らせ、考察が楽になるときがあります。
空集合に関連して注意する用語
高校一年の学習進度が進み、場合の数・確率を学習するときに、事象が互いに排反という言い方が出てきます。
この場合の数・確率の単元で、事象と言っているものは、まさに集合のことです。
そのため、事象という集合について、共通部分や和集合を考えたりします。
ここで気になるのが、「互いに排反」という用語です。
二つの事象(集合)A と B について、
A ∩ B が空集合となっているときに、A と B が互いに排反といいます。
ちょうど集合についての基礎的なことを学習しているときに、触れておくと、良い予習になるかと思います。
<具体例>
全体集合 U を 9 以下の自然数全体とします。
※ 場合の数・確率の単元では、この U を全事象といいます。
そして、A = {1, 2}, B = {5} とします。
この A と B は、
A ∩ B が空集合となっています。
そのため、A と B は互いに排反となっています。
今度は、C = {2, 5, 7} と A の共通部分を考えてみます。
2 だけが A と C の両方に含まれている要素です。
そのため、
A ∩ C = {2} です。
そのため、U における事象(部分集合)である A と C は、互いに排反ではありません。
高校数学では、様々な用語が出てきますが、定義の内容を理解し、適切に使うと自然と身につくかと思います。
ちょうど、共通部分と和集合を取り挙げたので、関連する内容として、「互いに排反」ということを押さえておくと、自然な流れで用語の内容が定着するかと思います。
また、U の要素だけれども、U の部分集合 A には含まれていないというものが現れるときがあります。
このような要素の考え方は、A の U における補集合の内容となります。
場合の数の前に補集合を押さえておくと、条件を満たさないということについて、補集合という部分集合を使ってイメージすることができるようになります。
ただ、この何通りということを数えるときに、集合に含まれる要素の個数を計算するときもあります。
そこで、場合の数の前の段階として、
個数定理を押さえておくと良いかと思います。
関連する内容を定義から着実に理解すると、高校数学の理論が使えるようになり、高度な考察ができるようになってくるかと思います。
高校一年のときは、聞き慣れない用語が多く出てくるかと思いますが、定義を着実に押さえ、典型的な命題が成立する過程を把握することが、良い土台づくりになります。
それでは、これで今回のブログ記事を終了します。
読んで頂き、ありがとうございました。