オイラーの多面体定理 | へこみのない凸多面体【treeを使う証明も】
" オイラーの多面体定理 “を用いた具体的な考察と木(tree)を用いた証明を書いています。
厳密証明はグラフ理論の基礎的な内容を使います。一応、証明を書いていますが、旧課程の高校数学では定理を使えれば大丈夫という内容だったので、参考程度に。
凸多面体の頂点数、辺の本数、そして面の数について、必ず成立する関係式を使って、未知の数字を求めることを考えています。
役に立つ関係式なので、立方体などのよく知っている図形を通して練習しておくと良いかと思います。
オイラーの多面体定理 :こんな等式が成立
【オイラーの多面体定理】
凸多面体の頂点の個数を v, 辺の本数を e, 面の個数を f とします。
このとき、v － e + f = 2 となります。
オイラー (Euler) の多面体定理によって、
v － e + f = 2 の等式が必ず成立します。
この関係を利用して、まだ不明な個数を求めることができます。役に立つので、具体例を用いて慣れておくと良いかと思います。
ちなみに、凸多面体とは、いくつかの平面で囲まれた多面体で、へこみのないものです。
立方体などが具体例になります。算数や中学一年の数学で具体的な例を学習しています。
よく知っている空間図形である立方体を通して練習してみます。
立方体で確認
立方体はサイコロなので、面の数は 6 個です。オイラーの多面体定理の f = 6 ということです。
少し図を描いてみて、頂点の個数が 8 個あることが分かります。
v = 8 です。
それでは、等式から辺の本数 e を求めます。
多面体定理より、
v － e + f = 2
8 － e + 6 = 2
14 － e = 2 より、－e = －12
すなわち、e = 12
これで、辺が 12 本あることが分かりました。直接、図から分かりにくい数を等式を利用して求めることができるので、役に立ちます。
凸多面体だと必ず成立する等式というのが強力です。
今度は、正八面体で考えることにします。
オイラーの多面体定理 :さらに具体的に練習
図形を軽く描いて、分かる個数を確認し、図から明確に個数が分からない残りをオイラーの多面体定理で求めます。
今度は正八面体です。八面体という名前から、面が 8 個あるということが分かります。
次に、図から頂点の個数を数えます。
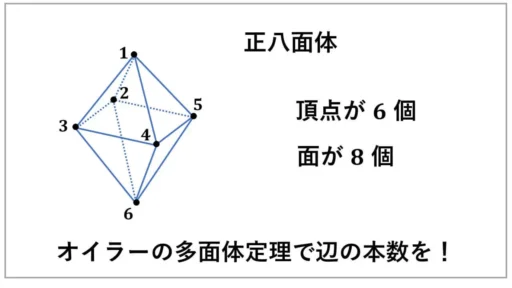
頂点の個数 v = 6 ということが図から分かりました。
f = 8 が面の個数なので、オイラーの多面体定理から、残りの辺の本数を求めることができます。
多面体定理より、6 － e + 8 = 2
よって、e = 12
これで辺が 12 本あるということが分かりました。
さらに、複雑な凸多面体で練習をしてみます。正二十面体を考えます。
これについては、図を描くのが大変です。こうなってくると、論理的に理で考えます。
正二十面体で
【正多面体の辺の数】
1 つの面の辺の本数 × 面の数 ÷ 2
図を描くのが困難な正二十面体については、この命題を使います。証明をまずしておきます。
＜証明＞
1 つの面にある辺の本数に面の数だけ乗じます。
そのときに、1 つの面にある各辺は、隣接する他の面と 1 本の辺を共有することから、2本が重なります。
→ そのため、2 で割ると、多面体の全ての辺の総数となります。【証明完了】
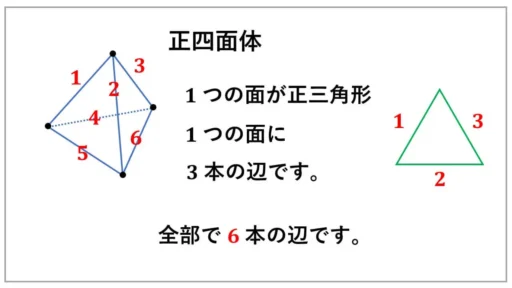
抽象的な証明なので、内容を正四面体で確認します。
1 つの面に辺が 3 本あります。
面の数は 4 個です。
3 × 4 = 12 （本）ですが、1 つの面にある 3 本の辺は、必ず他の面の辺と重なっています。
そのために、重複する 2 本を 1 本と考え、
3 × 4 ÷ 2 = 6 （本）
確かに正四面体の辺の総数は 6 本です。
この ÷2 の部分は、理解するのが難しいです。
そこで、次の展開図で印象に残しておくのがオススメです。
テストのときなどに使うときに、「あっ ÷2 をしないと」と気づけるようにするために正四面体の展開図で記憶に残しておくのが良いかと。
展開図を組み立てたときに、同じ色の辺と辺が重なって一つの正四面体の辺となります。
展開図の正三角形たちを切り離すと、1 つの正三角形に辺が 3 本あります。
面が 4 つあるので、3 × 4 で 12 本の辺がある状態です。
組み立てたときに、同じ色の辺と辺が 1 本の辺となるので、÷2 をするというわけです。
そのために、12 本の辺が 2 で割られ、6 本になります。
では、ここからは正二十面体の頂点の個数を求めることを目指します。
今証明した命題を利用して、面の数から辺の数を求めます。
その後で、オイラーの多面体定理を使います。
面の個数 f = 20 は名前からすぐに分かります。まず、正二十面体の辺の数を求めます。
正二十面体は、それぞれの面が正三角形となっています。
そのため、1 つの面の辺の数は 3 ということになります。
よって、3 × 20 ÷ 2 = 30
これで、辺の本数が 20 本と分かりました。
e = 30 です。辺と辺が重なることから 2 で割るので注意です。
残りの頂点の個数 v をオイラーの多面体定理で求めます。
v － 30 + 20 = 2 より、v = 12
これで、正二十面体の頂点の個数が 12 個と分かりました。
この 1 つの面の辺の本数から正多面体の辺の本数を求める計算方法を使うためには、1 つの面がどの形をしているのかということを知っておく必要があります。
幸い、中学 1 年の立体図形の内容で学習していますので、それらをまとめておきます。
・正四面体 – 各面は正三角形
・立方体 – 各面は正方形
・正八面体 – 各面は正三角形
・正十二面体 – 各面は正五角形
・正二十面体 – 各面は正三角形
では、同じ要領で正十二面体についても考えてみます。
まずは辺の本数を面の個数から求めます。
正十二面体
十二面体なので、面の数は f = 12 です。
各面が正五角形なので、1 つの面の本数が 5 本です。
このことから正十二面体の辺の本数を求めます。
5 × 12 ÷ 2 = 30 です。
これで、辺の本数 e = 30 が求まりました。
残りの頂点の個数 v を、オイラーの多面体定理で求めます。
v － 30 + 12 = 2 より、v = 20
これで頂点の個数が求められました。
ここまで、オイラーの多面体定理を使ってきました。
この厳密証明をグラフ理論を使って行います。ただ、そのためにはグラフ理論の基礎的な土台が必要になります。
あくまで参考程度に、さらっと証明を書いておきます。
オイラーの多面体定理 :木を使った証明
閉路を含まないグラフを林 (forest) と定義し、連結な林を木 (tree) と呼びます。
多面体を外球面に投影してできるグラフが平面的であるということで、オイラーが1750年に証明した定理です。
G を連結平面グラフの平面描画とする。
その点数を v、辺数を e、面数を f とする。
このとき、v － e + f = 2
＜証明＞
G の辺数 e についての帰納法で証明をします。
e = 0 ならば、G は連結なので、v = 1 で、無限面しかないので f = 1 となります。
そのため、e = 0 のときには、等式が成立しています。
e － 1 本以下の辺をもつすべてのグラフに対して、定理が真であると仮定し、e 本の辺があるグラフ G を考えます。
もし G が木 (tree) ならば、e = v － 1 かつ f = 1 なので、v － e + f = 2 が成立します。
よって、以下で G が木でないときを考えます。
G が木でなければ、G の閉路に含まれる 1 つの辺を e とすると、G － e は連結平面グラフです。
v 個の頂点、e － 1 本の辺、f － 1 個の面があります。
よって、帰納法より、
v － (e － 1) + (f － 1) = 2
左辺を整理すると、v － e + f = 2
これで証明が完了しました。
とはいえ、この証明の内容を理解するためには、グラフ理論の基礎となる内容を把握しなければなりません。あくまで参考です。
高校数学で、オイラーの多面体定理は証明はカットされているので、厳密証明よりも、実際に練習問題などで使って慣れることが大切かと思う次第です。
ただ、証明の骨格を押さえておくのは、良いかと思います。
グラフ G の辺の本数 e についての数学的帰納法を用いた証明です。
そのため、大枠（アウトライン）は ①「e = 0 のときに成立」と②「e ≧ 1 のとき、e － 1 まで命題が成立すると仮定すると e のときにも命題が成立」となります。
①を先に示しておかないと、e = 0 のときは e － 1 についての命題が定義できません。
e = 0 のときに命題が成立するということを先に示しておけば、以下は e ≧ 1 として議論ができます。
そうすると、②の仮定を述べることができます。
さらに、②の内容は、「G が木のとき」と「G が木でないとき」に場合分けをしています。
数学では、条件を満たすか、満たさないかのどちらかに必ずなるので、どちらの場合についても命題が成立するということを示しています。
これで、起こり得るすべての場合について命題（オイラーの定理）が真ということが数学的帰納法で示せたことになります。
グラフ理論については、ケーニスベルグの橋とオイラーが有名です。
大学で代数学を専攻するときには、リー代数を学習するときに、ディンキン図形でグラフ理論の基礎的な内容を使います。
余裕があるときに、グラフ理論の基礎的なことを押さえておくのも良いかと思います。
大学で扱われる複素函数論の内容で、複素数についての指数関数と複素数についての三角関数を結びつける重要な定理になります。
今回扱ったように、関係式（等式）を利用して議論を進めることは大切なので、慣れておくと良いかと思います。
関係式を作る公式として、
平行線と線分の比という記事で、メネラウスの定理について解説しています。
それでは、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。