Inclusion | 埋め込みという同型について既知の例を使い解説

2022年4月11日

Inclusion （埋め込み）について、高校数学までで既に学習している例を使って解説をしています。代数構造についての内容を、知っている身近な例を通して説明をしています。

抽象的なものを具体的に理解できるように心がけて記述したブログ記事になります。

特に、線形同型写像であり、環としての同型写像でもある対応を取り挙げています。

複素数について、高校数学の復習になりつつ、大学などで扱われる代数学の基本となる内容へと話を展開していきます。少しでも、代数学の理解になれれば幸いです。

Contents

1. Inclusion :線形写像から
- 1.1. 具体的な代数で様子を見る
- 1.2. Inclusion のイメージ
2. Inclusion :代数として
3. Inclusion :大学の三年次の内容
- 3.1. 根となっていることの確認

Inclusion :線形写像から

数学において、inclusion（埋め込み）といったときに、様々なタイプのものがあります。

まずは、大学の数学で、すぐに学習する線形代数についての埋め込みから解説をしていきます。
　
代数学を学習していくときに、次の意味で線形代数は基本的と考えられます。線形代数において、加法とスカラー倍が定義されていますが、さらに加法とは異なる二項演算である積（乗法）が定義されるときがあります。
　
そのときに、単なる線形代数ではなく、積のことまで考えて、algebra（代数）と呼ばれます。
　
algebra において、積について、結合法則が成立するときに、結合代数といわれます。非可換なものは、さておき、積について交換法則が成立するもので、身近なもの考えてみます。

具体的な代数で様子を見る

【定義】

A と B を体 K 上の線形代数（ベクトル空間）とする。
f : A → B が線形写像であり、かつ f が単射であるとき、f を A から B への線形写像としての inclusion（埋め込み）という。

このように、大学の数学を学習するときに、いきなり抽象的な定義が出てくることが多いです。

そんなときこそ、平易な具体例を通して内容を確認することが大切になるかと思います。具体例を通して考えると、意外と自分がこれから扱っていけそうだと思えたりするときもあります。

実数全体 R は、体 R 上の線形代数です。そして、複素数全体 C も体 R 上の線形代数です。定義の A と B として、それぞれ R と C を当てはめて、以下で議論を進めていきます。

線形写像 f : R → C を次のように定義します:

f(r) = r + 0 × i ∈ C（ただし、r ∈ R, i は虚数単位）

ここで、0 × i は 0 なので、f(r) = r と表記するようにします。
※ 線形代数（ベクトル空間）のスカラー倍や加法についての公理は、このリンク先で細かい部分を解説しています。

x, y ∈ R に対し、f(x+y) = x+y = f(x)+f(y) であり、c ∈ R に対して f(cx) = cx = cf(x) となっているので、f は線形写像です。

さらに、x₁, x₂ ∈ R について、x₁ ≠ x₂ であるとき、f(x₁) = x₁ ≠ x₂ = f(x₂) です。

これは、f が単射ということを示しています。

Inclusion のイメージ

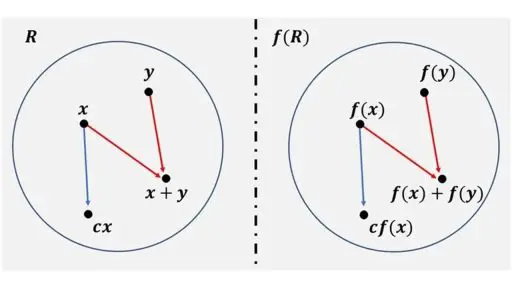
f(R) = {f(x) | x ∈ R} を R の f による像といいます。高校数学で、値域といっていた対応する値をすべて集めた集合です。今、R を R 上の線形代数として考えています。

代数的な二項の対応としては、加法とスカラー倍を考えています。

f は、inclusion の定義を満たしていました。このときに、どうなっているのかというと、R と f(R) が、R 上の線形代数として、同じ構造をしていると考えられます。

x, y に対し和 x + y

f(x), f(y) に対し和 f(x) + f(y)

加法について、x と y の表面的な見た目が f(x) と f(y) になっているだけです。

見た目が異なるだけで、本質的な二項演算の規則として、同じ加法となっているということです。

2 + 3 = 5
f(2) + f(3) = f(5)

スカラー倍についても、見た目が x と f(x) と異なる表記になっているだけで、本質は同じです。

x ∈ R, c ∈ R に対し、スカラー倍 cx
f(x) ∈ R, c ∈ R に対し、スカラー倍 cf(x)

加法やスカラー倍の定義には、直積集合の元である組に値が対応させられているのですが、見た目の記号を x は f(x) と置き換えると、同様のことが起きていることになります。

※ 直積集合についての詳細は、リンク先に書いています。

この見た目の表記が異なるだけで、線形代数として同じ構造物であることを線形代数として同型といいます。そのため、R と f(R) は線形代数として同型ということになります。

ここで、f : R → C でした。

それゆえに、f(R) ⊂ C となっています。そして、R と f(R) は、R 上の線形代数として同じ構造をしています。
　
このことから、R 上の線形代数として、R と同じものが C の中に内蔵されていると考えられます。

このことを、f による R の埋め込みといいます。英語で書くと、included されているということです。写像という名詞として、inclusion と呼んでいます。

抽象度が上がってきたので、もう少し具体的に内容を反復します。

はじめに、r ∈ R に対して、f(r) = r + 0 × i と定義しました。

虚部が 0 なので、f(r) = r としました。これは、同型だからこそできる略記です。

r₁, r₂ に対し、和 r₁ + r₂
f(r₁), f(r₂) に対し、和 (r₁+0i) + (r₂+0i)

r₁ と f(r₁), r₂ と f(r₂) と、表面的な見た目が違うだけで、本質的に同じ加法を計算しているということになります。スカラー倍についても、cr と c(r + 0i) は本質的に同じということです。

Inclusion :代数として

線形代数であって、さらに積（乗法）という加法とは異なる二項演算が定義されているときに algebra（代数）ということでした。

R と f(R) ⊂ C について、積も考えて、algebra としての同型について様子を見てみます。
※ただし、この algebra は R 上の代数として考えています。

そこで、複素数全体 C における乗法という二項演算を確認しておきます。

a, b, x, y ∈ R について、
(a + bi)(x + yi)
= (ax – by) + (bx + ay)i

※ 実部と虚部などの複素数についての基本事項は、リンク先の以前に書いた記事にまとめています。

r₁, r₂ ∈ R について、R における乗法の結果である積は、r₁r₂ です。

f : R → C について、f(r₁), f(r₂) ∈ C における複素数どおしの乗法を確認すると、
f(r₁)f(r₂) = (r₁ + 0i)(r₂ + 0i)
= r₁r₂ + 0i と分かります。

少し見た目が違っているだけで、0i を省略してしまうと、
f(r₁)f(r₂) = r₁r₂ です。

やはり本質的に同じ乗法についての対応規則になっています。R における乗法は、交換法則が成立するので、可換代数といわれます。

※ 複素数の乗法に関して、乗法逆元については、複素数の除法という記事で高校数学の内容で詳しく解説をしています。

可換代数として、R と f(R) は同型です。

そして、f(R) は、C の中に埋め込まれているということになります。

そのため、R 上の可換代数 C の中に、f(R) として R が埋め込まれています。

同一視について

大学の数学を学習していると、「同一視する」という内容が出てくるときがあります。

難しい抽象的な内容を扱っているときに、この同一視を初めて見ると、何のことかよく分からなくなってしまうと思います。昔の私もそうでした。

そうならないように、先ほどの例を同一視の例として認識をしておくと、その他の内容の理解への足掛かりになるかと思います。

f(R) = { r + 0i | r ∈ R} は、複素数全体 C の真部分集合になっています。ここで、同一視という聞き慣れない言葉を使うと、「r + 0i を r と同一視する」といいます。

これは、先ほどの埋め込みについて、F(R) と R が R 上の可換代数として同型ということからできる見なし方です。

R 上の可換代数としての振る舞いが同じなので、r + 0i のことを R と考えてしまうということです。

(r₁ + 0i) + (r₂ + 0i) と記述するのは、やや面倒なので、表面的な記号の違いを無視します。

そうすると、r₁ + r₂ と本質的に同じ加法の振る舞いなので、いっそ r₁ + r₂ と記述します。（ただし、r₁, r₂ ∈ R）

積や R からのスカラー倍についても同じく表面的な記号の書き方が違って見えているだけです。本質的な可換結合代数としての扱いは、f(R) も R も同じ振る舞いです。

それゆえに、いっそ f(R) のことを R としてしまうということです。

この同一視は、高校の数学のときに、複素数の計算でよくしていました。

(2 + 0i) + (3 + 0i) = 5 + 0i
2 + 3 = 5

上の書き方は、複素数全体を R 上 2 次元の可換結合代数と考えたときの定義通りの計算です。

しかし、やや記述するのが面倒に感じます。R と f(R) を同一視して、下の「2 + 3 = 5」のようにすると、すっきりします。

複素数平面を埋め込む inclusion

R × R = {(x, y) | x, y ∈ R} は xy-座標平面です。複素数平面について、高校の数学で学習をします。この複素数平面を R² と表すことにします。

一方、C = {x + yi | x, y ∈R } という複素数全体も、R² と同じく、R 上 2 次元のベクトル空間となっています。

f : R² → C を
f((x, y)) = x + yi と定義することで、R 上の線形代数として同型になります。

C については、複素数どおしの乗法が定義されていました。

つまり、
(x₁ + y₁i)(x₂ + y₂i)
= (x₁x₂ – y₁y₂) + (x₁y₂ + y₁x₂)i

高校数学では、複素数平面において、乗法が定義されていませんでした。しかし、回転運動を複素数についての乗法を利用して表しています。

複素数平面（xy-座標平面/ガウス平面）において、乗法が定義されていなかったので、平面上の点に対応する複素数を考え、複素数についての乗法を C において行っていました。

そして、乗法の結果として得られた複素数を再び平面上の点と対応させることをしていました。この一連の操作をショートカットするように、逆算思考で複素数平面 R² に乗法を定義します。

乗法は二項演算なので、直積集合 R² × R² から R² への写像を定義することになります。

p : R² × R² → R² を
p((x₁, y₁), (x₂, y₂))
= (x₁x₂ – y₁y₂, x₁y₂ + y₁x₂) と定めます。

写像（関数）の記号を使うと複雑に見た目がなるので、「×」の記号を使って乗法を表すことにします。

(x₁, y₁) × (x₂, y₂)
= (x₁x₂ – y₁y₂, x₁y₂ + y₁x₂)

これで、複素数平面 R² の 2 点について、その座標を使って、直接に乗法が計算できるようになりました。

先ほどの線形代数としての同型写像 f について、algebra としての積が保存成立します。

f((x₁, y₁) × (x₂, y₂))
= f((x₁x₂ – y₁y₂, x₁y₂ + y₁x₂))
= (x₁x₂ – y₁y₂) + (x₁y₂ + y₁x₂)i

一方、
f((x₁, y₁))f((x₂, y₂))
= (x₁ + y₁i) × (x₂ + y₂i)
= (x₁x₂ – y₁y₂) + (x₁y₂ + y₁x₂)i

f((x₁, y₁) × (x₂, y₂)) = f((x₁, y₁))f((x₂, y₂)) と確かになっています。どちらも同じ値の複素数になっています。

これで、f(R²) を C の中に埋め込めました。ただ、この像 f(R²) は C に一致しています。

この像が行き先の集合と一致するとき、つまり全射であるときに、同型写像といいます。

数と1行1列の行列を同一視する

埋め込みや同型写像の考え方は、基本的になります。行列と数は、それぞれ異なる集合に属しています。

しかし、議論を進めていく上で、数と 1行1列の行列を同じものだと見なしておくと便利なときもあります。

a ∈ C という複素数を (a) という 1行1列の行列に対応させることで、同型写像となります。複素数全体 C は複素数体 C 上の 1 次元の可換結合代数です。

しかも、0 ではない元は、乗法についての逆元を持ちます。

(a) という複素数を成分とする 1行1列の行列全体も、複素数体 C 上の 1 次元の可換結合代数です。

零行列でない行列は、a ≠ 0 という複素数を成分とする行列なので、(a) の逆行列は (a^-1) です。

(a)(a^-1) = (a^-1)(a) = (1)

(1) が、乗法についての単位元です。

g(a) = (a) という写像を考えると、明らかに同型写像となります。そのため、a と (a) を同一視するということが可能となります。
　
【関連する内容】
今回の内容で扱った同型対応のことを英語では、isomorphism といいます。線形代数と可換代数についての同型対応の具体例を上で述べました。

この同型ですが、準同型写像 f が単射であるときには、im f と同型になります。このときには、行き先の代数の中に im f として埋め込まれたことになります。

ここで、「単射であること」と、「核という ker f が {0} だけからなるイデアルであること」が同値になるということを押さえておくと、次のような発想をもつことができます。

準同型定理という定理があります。

このことと、inclusion の考え方をつなげて考えます。準同型定理を、単射でないときの埋め込みを行うときの考えとして押さえておくことができます。

最後に、他のブログ記事で、やり残している体論の細かい証明を述べておきます。

Inclusion :大学の三年次の内容

T ⊂ F[t] に体 F[x]/(f(x)) の構造を導入するという内容の細かい証明部分になります。
※ 分解体と代数的閉包の存在証明というブログ記事の中で使う内容になります。

まず、加法 +’ の交換律を示します。

g(t) +’ h(t)
= Ψ^-1(g^Ψ(t) + h^Ψ(t))
= Ψ^-1(h^Ψ(t) + g^Ψ(t)) = h(t) +’ g(t)

×’ の交換律も先ほどの +’ を ×’ に置き換えて同様の計算をすると確認できます。

また、h(t) = 0 のとき、h^Ψ(t) = [0] なので、h(t) = 0 が +’ についての単位元と分かります。

また、g(t) = Σ_ia_itⁱ のとき、
h(t) = Σ_i(-a_i)tⁱ とすると、h^Ψ(t) = [Σ_i(-a_i)tⁱ] が [Σ_ia_itⁱ] の加法についての逆元となっていることが確かめられました。

同様に考えて、h(t) = 1 とすると、[1] が F[x]/(f(x)) の乗法についての単位元なので、×’ についての単位元ということが分かります。
　
g(t) ∈ T が 0 でないとき、Ψ の定義（基底の一次結合の一意性）から g^Ψ(t) ≠ 0 なので、g^Ψ(t) には乗法についての逆元が存在します。

その逆元を Σ_i[b_i][xⁱ] とすると、Ψ^-1(Σ_i[b_i][xⁱ]) が g(t) の ×’ についての逆元となります。

実際、
g(t) ×’ Ψ^-1(Σ_i[b_i][xⁱ])
= Ψ^-1(g^Ψ(t)(Σ_i[b_i][xⁱ]))
= Ψ^-1([1]) = 1

1 が T において ×’ の単位元だったので、確かに Ψ^-1(Σ_i[b_i][xⁱ]) が g(t) の ×’ についての逆元ということが分かりました。

×’ についての結合律を確認します。Ψ と Ψ^-1 の写像の合成が恒等写像となることを使います。

g(x), h(x), k(x) ∈ T に対して、

g(t) ×’ (h(t) ×’ k(t))
= g(t) × Ψ^-1(h^Ψ(t)k^Ψ(t))
= Ψ^-1(g^Ψ(t)(h^Ψ(t)k^Ψ(t)))
= Ψ^-1((g^Ψ(t)h^Ψ(t))k^Ψ(t))
= Ψ^-1(g^Ψ(t)h^Ψ(t)) ×’ k(t)
= (g(t) ×’ h(t)) ×’ k(t)