虚数と複素数の違い | 異なる定義を確実に認識をして誤解なく!
" 虚数と複素数の違い “について、基本となる内容を解説しています。
虚数と複素数が、異なる定義であるということを認識することで、誤解なく数学の学習ができるかと思います。
また、複素数について、よく使う性質を定理として証明しています。
虚数単位 i という二乗すると -1 となる数を導入して、実数全体よりも広い範囲の数を考えることになります。
この虚数単位は、どの実数にどんな実数を掛けても一致しません。
このような数の範囲を考えるときに、集合を意識すると明確に違いが認識できます。
この記事では、虚数単位を i と表しています。
それでは、基礎となる定義から説明をしていきます。
虚数と複素数の違い :まずは定義から
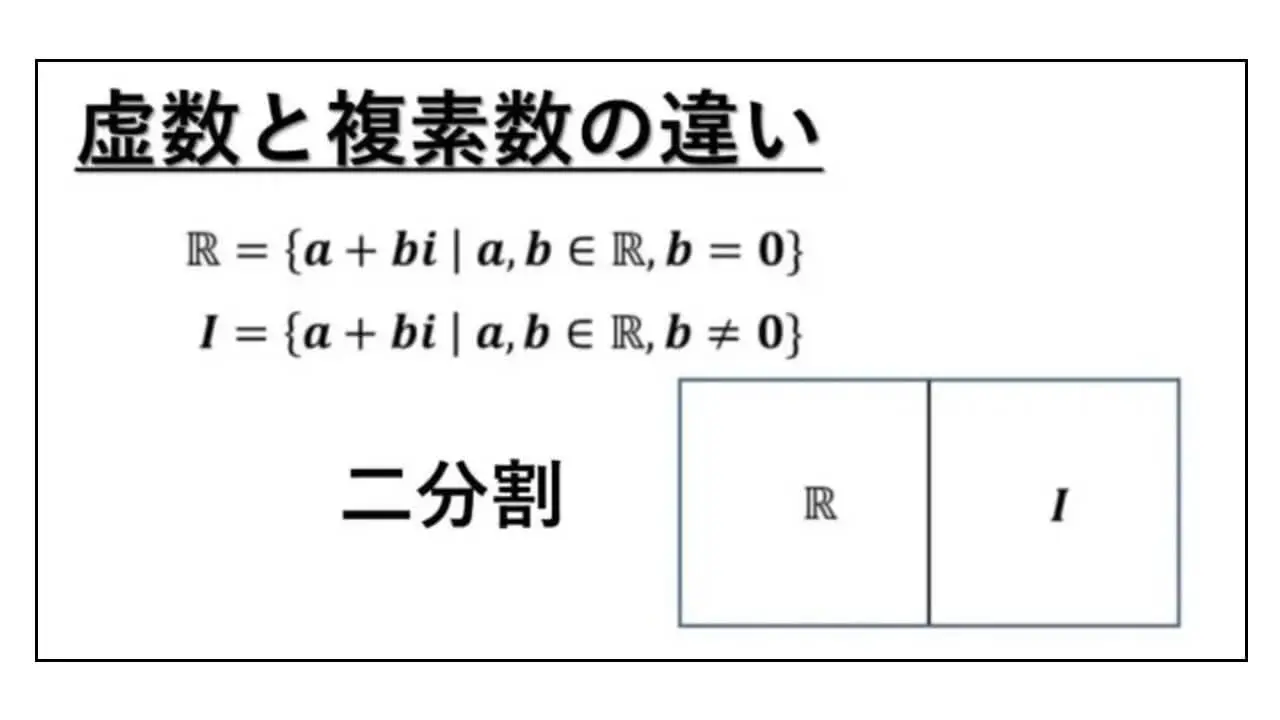
実数全体を R と表すことにします。
ここで、先ほどの虚数単位 i を実数倍してできる数と実数の和をすべて集めます。
その集合を次のように置いておきます。
{a + bi | a, b ∈ R, b ≠ 0}
= I
この集合を I と表すことにします。
この集合 I に含まれている数のことを虚数といいます。
虚数単位を実数倍している b が、ゼロではない実数ということです。
a の値に関わらず、b の実数がゼロではないときに、虚数といいます。
また、I の要素の表し方ですが、
b = 0 のときに、
a + bi = a とシンプルに表します。
b = 0 のとき、通常の実数ということになります。
論理的に、b の部分は、0 であるか、0 ではないかのどちらかになります。
{a + bi | a, b ∈ R, b ≠ 0}
が実数全体 R となっています。
「0 である」か「0 でない」かのいずれか一方のみが成立するので、
R ∩ I は空集合となっています。
そのため、
虚数全体 I と R ∪ I は異なる集合ということが分かりました。
集合を使って表す
複素数全体が、どういう数の集合かということを表すと、
R ∪ I となります。
実数全体と、虚数全体の和集合です。
しかも、実数全体と虚数全体の共通部分は空集合ということです。
このことから、複素数が一つ与えられたときに、次の二つの場合に分けられます。
① その複素数は実数で R の要素
② その複素数は虚数で I の要素
a + bi という複素数が与えられたとき、
① a + bi ∈ R ならば、b=0 です。
一方、a + bi という複素数が与えられたとき、
② a + bi ∈ I ならば、b ≠ 0 です。
R = {a + bi | a ∈ R, b = 0},
I = {a + bi | a, b ∈ R, b ≠ 0}
複素数全体は、R ∪ I と二分割されています。
※ R ∩ I は空集合となっています。
この複素数全体の二分割は、シンプルです。虚数単位を実数倍している実数が、0 であるか、0 ではないかというだけです。
ここで、よく虚数と複素数を混同する原因になる定義を書いておきます。
複素数 a + bi について、
a = 0 かつ b ≠ 0 のとき、この複素数を純虚数といいます。
純虚数は先ほどの集合 I に真に含まれています。
虚数全体 I の中で、この純虚数は虚数単位にゼロではない実数を掛けたものという特別な形をしたものです。
昔からよく言われる誤解を書いておきます。
「純虚数でない複素数」だから実数とすぐに考えると誤りになります。
「純虚数ではない複素数」といったときに、次の三つの場合が考えられます。
a + bi について
① 「a ≠ 0, b ≠ 0」 の場合
② 「a ≠ 0, b = 0」 の場合
③ 「a ≠ 0, b = 0」 の場合
つまり、
「純虚数ではない複素数」といったときに、
「虚数の範囲内」だと、
①「a + bi (a≠ 0, b≠ 0) の場合」ということです。
残りの②と③の二つは、
「純虚数ではない複素数」が「実数の範囲内というときの場合」です。
用語ですが、a + bi について、a のことを実部といいます。
そして、b のことを虚部といいます。
さらに、複素数 a + bi がゼロであるということは、実部の値がゼロで、虚部の値もゼロということです。
つまり、a + bi = 0 とは、
a = 0 かつ b = 0 ということです。
※ この内容は、複素数の相当に関わってきます。
ここから、複素数の絶対値について説明します。
虚数と複素数の違い :大きさは絶対値

複素数 z = a + bi について、複素数の大きさである複素数の絶対値の定義です。
複素数平面でいうところの原点から点 (a, b) までの距離ということになります。
b = 0 で虚数でないときでも、b に 0 を代入して使える絶対値の定義です。
また、複素数の議論をするときに、共役複素数というものが出てきます。
z = a + bi の共役複素数について、上にバーをつけて表します。
虚部のプラスとマイナスを逆転させたものになります。
複素数平面では、点 (a, b) と横軸である虚軸について対称な点が、点 (a, -b) ということです。
ちなみに、この定義から、z の共役複素数のそのまた共役複素数は、再びもとの z ということが分かります。
※ 虚部 b の符号を逆にしてから、さらに逆にしたということだから、もとに戻るということです。この共役複素数ともとの複素数の積が、絶対値に関連します。
z・z = (a+bi)(a-bi)
= a2+b2 = |z|2 です。
よって、z・z = |z|2 が成立します。
複素数の絶対値についての代表的な内容を説明したのですが、実数についての絶対値も押さえておくことが大切になるかと思います。
一次元の数直線における絶対値についての距離を複素数平面における距離に拡張したものとなっています。
虚数と複素数の違い :共役複素数の性質
ここまで、複素数 z の共役複素数を上にバーをつけて表してきました。
ここから、大学の数学も見越して、関数の対応で複素共役を表してみます。
z = a + bi (a, b は実数)に対して、
a - bi という複素数を対応させるということは、関数の対応になります。
複素数に対して複素数を対応させるというこの複素関数を f と表すことにします。
f(z) = a - bi が対応する共役複素数です。
すると、二つの複素数 z1 と z2 の加法と乗法について、次の (1) と (2) が成立します。
f(z1 + z2) = f(z1) + f(z2) … (1)
f(z1z2) = f(z1)f(z2) … (2)
共役複素数が出てきたときの複素数の計算で、基本となる関係です。
これから、それぞれを証明します。
これらの等式は、
z1 = a + bi, z2 = c + di というように、実数 a, b, c, d を使って表して直接計算をすると、左辺と右辺がどちらも同じ式になることが確認できます。
まず上の (1) 式についての証明を書きます。
下の (2) 式も、分配法則で計算をすると得られます。どちらも実部と虚部を整理する形でそろえることが、大切になります。
上の (1) 式についての証明で、実部と虚部を整理します。
z1 + z2 = (a + c) + (b + d)i なので、
両辺の共役複素数をとると、
f(z1 + z2) = (a + c)-(b + d)i です。
一方、
f(z1) = a-bi, f(z2) = c-di だから、
f(z1) + f(z2) = (a + c)-(b + d)i
これで、
f(z1 + z2) と f(z1) + f(z2) が同じ値となったので等しいということになり、
f(z1 + z2) = f(z1) + f(z2) と、
(1) を示すことができました。
全体に共役複素数をとる前に、z1 と z2 の加法を計算しておいてから、虚部の実数のプラスとマイナスを逆転させるのが左辺です。
その結果は、先に共役複素数をとっておいた二つの加法と同じになるということです。
(2) 式については、これを乗法について計算して確かめるということになります。
次に、
z1 = a + bi, z2 = c + di の積について (2) を証明します。
これも、分配法則を中心として実部と虚部を整理するということで導くことができます。
z1z2 = (a + bi)(c + di)
= (ac - bd) + (ad + bc)i
すべてイコールでつながっているので、どれも同じ複素数になります。
したがって、共役複素数はすべて等しくなります。
特に、はじめの式と、最後の式で共役複素数は等しくなることに注目します。
f(z1z2) = (ac – bd)-(ad + bc)i
一方、
f(z1)f(z2) = (a-bi)(c-di)
= (ac – bd)-(ad + bc)i
どちらも同じ値となったので、
f(z1z2) = f(z1)f(z2) です。
これで、示したかった (2) の等式に辿り着けました。
実数係数の方程式と共役解
共役複素数をとることと、加法や乗法について成立する内容を示しました。
これらを使って、
「実数係数の方程式が虚数解をもつときに、その共役複素数も解となるということ」が示されます。
an, an-1, ・・・, a1, a0 を実数とし、これらを係数とする次のような n 次の方程式の解についての定理です。
anxn+an-1xn-1+…+a1x1+a0=0
これを実数係数の n 次方程式といいます。
α という虚数が、この方程式の解だとします。
つまり、x = α を方程式に代入すると、左辺と右辺の値が等しいということです。
このときに、α の共役も、方程式の解になることが、次のようにして証明されます。
先ほど示した、共役をとること加法や乗法についての内容を使います。
α は解なので、
anαn+an-1αn-1+ … + a1α+a0 = 0
両辺が同じ複素数なので、
共役をとるという関数 f で対応する値は同じになります。
そして、0 は実数なので、f(0) = 0 だから、
f(anαn+an-1αn-1+ … + a1α+a0) = 0
先ほど示した (1) から、
加法について、
f(anαn)+f(an-1αn-1)+ … + f(a1α)+f(a0) = 0
(2) から、乗法について、
f(an)f(αn)+f(an-1)f(αn-1)+…+f(a1)f(α)+f(a0)=0
ここで、各 ai は実数なので、
複素共役をとっても値が同じことから、
anf(αn)+an-1f(αn-1)+ … + a1f(α)+a0 = 0
さらに、
(2) を用いて累乗の部分を計算すると、
anf(α)n+an-1f(α)n-1+ … + a1f(α)+f(a0) = 0
これは、α の複素共役 f(α) が、
方程式 anxn+an-1xn-1+…+a1x1+a0=0 の解であることを示しています。
x に x = f(α) を代入すると、
anxn+an-1xn-1+…+a1x1+a0 が 0 となったので、解というわけです。
an, an-1, ・・・, a1, a0 は実数だったので、共役をとっても値はもとの実数のままということと、(1) と (2) の関係式を使い続けたことが効きました。
代入したときに、左辺と右辺が同じ値になっているということは、方程式の解ということになります。
これで、「実数係数の方程式が虚数解をもつときに、その共役複素数も解となるということ」 が証明できました。
ちなみに、厳密証明は大学の数学でなされるのですが、複素数を係数とする n 次の方程式は必ず複素数解をもつという代数学の基本定理が証明されています。
【他の複素数の記事】
■ 累乗根
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。