中間値の定理 | 高校数学IIIでの使い方と大学数学での証明
" 中間値の定理 “の使い方を高校の数学IIIでの典型的な例を用いて解説します。その後で、大学の数学における証明を述べています。
実数の連続性の公理に基づく証明は、高校では扱いませんが、大学の微積の理論を理解する上では大切になります。
高校の内容と大学の内容で、必要な部分をご覧頂ければ幸いです。
中間値の定理は、いかにも連続関数らしい定理です。
定理は難しそうですが、関数のグラフが連続で、つながっていることをイメージすると、使い方が見えてきます。
中間値の定理 :数３での使い方
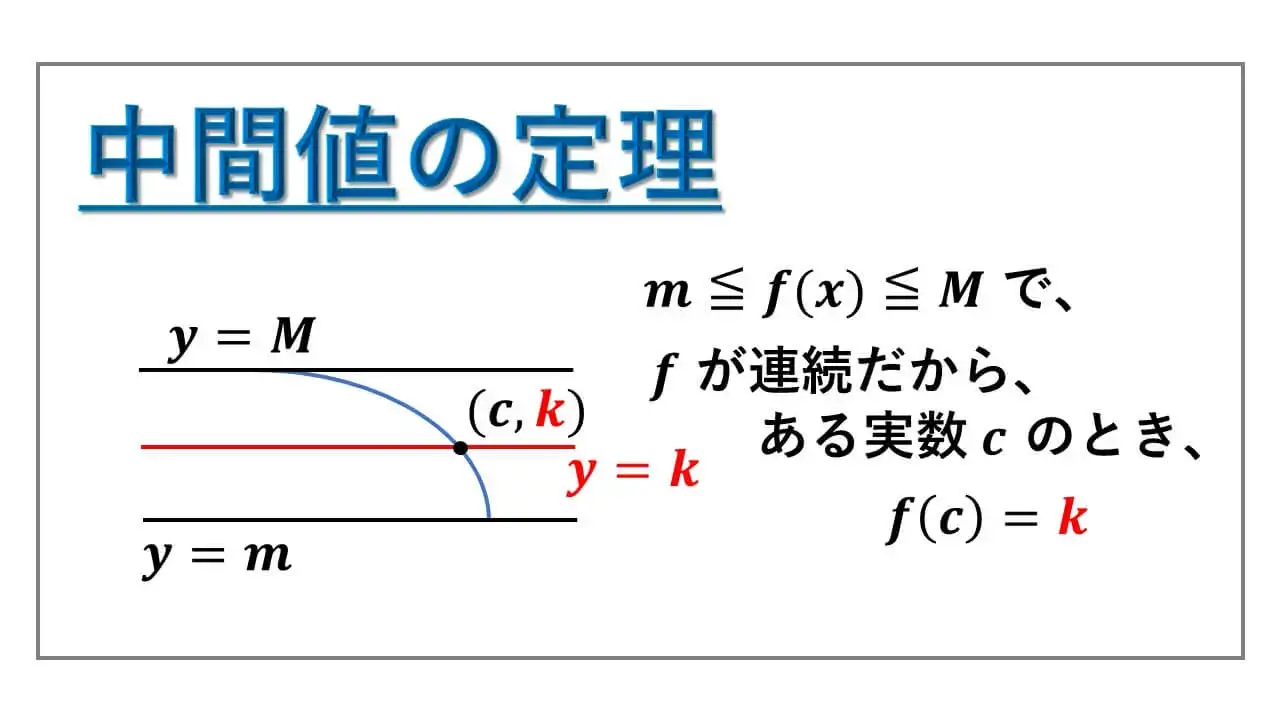
【中間値の定理】
実数値関数 f は閉区間 [a, b] で連続だとする。そして、この区間における f の最大値を M, 最小値を m とする。
M ≠ m ならば、m < k < M である任意の実数 k に対して、閉区間 [a, b] 内の点 c が存在して、f(c) = k
これが、中間値の定理です。
定理の結論以外の内容に当てはまる状況が出てきたら、定理を使うチャンスです。
具体的な連続である実数値関数で、定理を使ってみると、理解が深まるかと思います。
典型例で確認
f(x) = sin x + xcos x + 2 とする。
この連続関数は、閉区間 [0, π] 内のある点 c において、f(c) = 0 となる。
この関数 f は連続関数で、
閉区間 [0, π] における議論です。
この区間において、f(0) = 2,
f(π) = －π + 2 となっています。
つまり、連続関数 f は、[0, π] という閉区間において、－π + 2 から 2 までの値を必ずとるということになります。
実は、閉区間において定義されている関数は、必ず最大値と最小値をとるという「連続関数についての定理」が背後にあります。
※ この証明は、大学数学の内容になります。
そのため、[0, π] における最小値を m, 最大値を M とおくと、
m ≦ －π + 2 < 2 ≦ M となっています。
そのため、中間値の定理の k として、
m < k = 0 < M を考えることができます。
よって、中間値の定理から、[0, π] 内のある点 c において、f(c) = 0 となります。
この中間値の定理を使った内容を、もう少し丁寧に述べます。
f は連続なので、値域において、
－π + 2 から 2 までの値を必ずとるため、
その間にある 0 という値をどこかでとることになるというわけです。
ここで、連続なつながっているグラフをイメージすると理解の手助けになります。
π は約3.14 なので、
f(π) = －π + 2 は負の実数です。
f(0) = 2 は正の実数です。
そして、f(x) のグラフは連続関数なので、値域において、－π + 2 から 2 までの値をすべて取ります。
そのため、特に 0 という －π + 2 と 2 の間にある値を必ず取っているということになります。
（縦軸の －π + 2 以上 2 以下の値を、連続関数だから全て取るという値域におけるイメージが大切になります。）
f(x) のグラフの概形は不明ですが、f(c) = 0を満たす実数 c が、閉区間 [0, π] の範囲内に存在するということになります。
ここまでが、高校の数学の内容です。
以下において、中間値の定理を大学の内容で証明します。
中間値の定理 :場合分けて証明
【実数の連続性の公理】
・上に有界な実数の集合は上限をもつ
・下に有界な実数の集合は下限をもつ【連続関数の定理】
ブログ連続関数の定理より
閉区間上で定義された実数値連続関数は、最大値と最小値をもつ
この連続関数についての最大値と最小値の存在定理を証明した後で、その定理を使って、中間値の定理を証明するという流れになります。
リンク先で、最大値と最小値をもつことの証明をしています。この記事では、この定理と実数の連続性の公理を使います。
場合分けをしつつ、いくつかの細かい命題を証明し、その結果として、中間値の定理が得られるという道筋です。
実数全体 R の空でない部分集合 S について、
実数 a が S のどの要素 x に対しても、
x ≦ a となっているときに、a を S の上界といいます。
S に上界が存在するときに、S についての最小の上界のことを S の上限といいます。
実数 b が S のどの要素 x に対しても、
b ≦ x となっているときに、b を S の下界といいます。S の最大の下界のことを、S の下限といいます。
命題1の証明
【命題１】
閉区間 I = [a, b] 上で定義された実数値連続関数 f が f(a) < 0 かつ f(b) > 0 だとすると、
c ∈ I が存在して、f(c) = 0
＜証明＞
A = {x | a ≦ x ≦ b, f(x) ≦ 0} とおきます。
f(a) < 0 だから、a∈A なので、A は空集合ではありません。
また、仮定より、b は A の上界なので、実数の連続性の公理から、A には上限が存在します。
よって、c = sup A とおき、c を A の上限とします。
（a ≦ c ≦ bとなっています。）
f(c) について、
[1] f(c) < 0, [2] f(c) > 0, [3] f(c) = 0 の場合が考えられます。
[1] f(c) < 0 の場合
仮定より、f(b) > 0 なので、b は A の上界で、b は A に含まれていません。
今、f(c) < 0 なので、
c ∈ A だから、c < b
仮定より、f は閉区間 I = [a, b] で連続だから、特に点 c において連続です。
ゆえに、正の実数 －f(c) > 0 に対して、正の実数 δ’ が存在して、「x∈I かつ |x － c| < δ’ ならば、|f(x) － f(c)| < －f(c)」となります。
※ これは大学数学で扱うイプシロンデルタ論法での連続関数の定義です。
ここで、 δ = min{|b － c|, δ} と置きます。
そして、x として、c + δ/2 を考えると、
|(c + δ/2) － c| = |δ/2| < δ なので、c + δ/2 は c を中心とする δ 近傍内に含まれていることになります。
つまり、|f(c + δ/2) － f(c)| < －f(c)
よって、f(c + δ/2) － f(c) < －f(c)
すなわち、f(c + δ/2) < 0
ところが、c < c + δ/2 であり、c は A の上限だったので、c + δ/2 は A に含まれません。
（c + δ/2 ∈ A とすると、c + δ/2 は、A の上限である c 以下になってしまいます。 ）
a ≦ c + δ/2 < c + δ ≦ c + (b － c) = b、
つまり、a ≦ c + δ/2 ≦ b であり、
かつ、c + δ/2 が A に含まれていないことから、f(c + δ/2) > 0
これは、f(c + δ/2) < 0 に矛盾です。
よって、[1] f(c) < 0 の場合は起こり得ないということになります。
[2] f(c) > 0 の場合
このとき、A の上限 c は A に含まれていません。
a は A に含まれていて、
b は A の上界だから、a < c ≦ b
点 c において f は連続だから、
f(c) > 0 という正の実数に対して、正の実数 δ が存在して、
x∈I かつ |x － c| < δ ならば、
|f(x) － f(c)| < f(c)
この x として、c － δ/2 を考えると、
|(c － δ/2) － c| = |－δ/2| < δ であるので、
|f(c － δ/2) － f(c)| < f(c)
つまり、－f(c) < f(c－δ/2)－f(c)
よって、移項すると、0 < f(c － δ/2)
A の定義より、c － δ/2 は、A に含まれないので、A の上界となります。
c は A の上限だから、c ≦ c － δ/2
しかし、δ > 0より、
c － δ/2 < c なので、これは矛盾です。
ゆえに、[2] f(c) > 0 の場合は起こり得ないということになります。
以上より、残りの可能性である [3] f(c) = 0 の場合になるということが結論づけられます。【証明完了】
この特殊な【命題１】を証明したことで、次の一般的な形の【命題２】が導かれます。
平行移動と対称移動を考えます。
命題２の証明
【命題２】
閉区間 I = [a, b] 上で定義された連続関数 f について、f(a) < k < f(b)となっているとする。
このとき、閉区間 I = [a, b] 内の実数 c が存在して、f(c) = k
＜証明＞
x∈I に対して、g(x) = f(x) － k とすると、
関数 g は閉区間 I = [a, b] 上で定義された連続関数であり、
f(a) < k < f(b) より、
g(a) < 0 かつ g(b) > 0
よって、【命題１】より、閉区間 [a, b] 内の実数 c が存在して、g(c) = 0
すなわち、f(c) － k = 0 より、
f(c) = k【証明完了】
今まで証明してきた定理は、閉区間の右端の点に対応する値の方が大きいという仮定でした。
仮定で、左端の方が大きいときにも成立するというのが次の【命題３】です。
ただ、このときは、x 軸について折り返すと【命題２】の形になるので、すぐに導かれます。
命題３の証明
【命題３】
閉区間 I = [a, b] 上で定義された連続関数 f について、f(a) > k > f(b)となっているとする。
このとき、閉区間 [a, b] 内の実数 c が存在して、f(c) = k
＜証明＞
x∈I に対して、g(x) = －f(x) とすると、
関数 g(x) は閉区間 I = [a, b] 上で定義された連続関数であり、
f(a) > k > f(b) より、
－f(a) < －k < －f(b)
つまり、g(a) < －k < g(b)
よって、【命題２】より、閉区間[a, b]内の実数cが存在して、g(c) = －k
すなわち、－f(c) = －k より、
f(c) = k【証明完了】
これらのことから、閉区間の両端の点に対応する値がことなれば、【命題２】と【命題３】 から、f(a) と f(b) の間の大きさの実数 k に対して、閉区間内の点 c が存在して、f(c) = k となるということです。
このことをまとめたのが最終的な「中間値の定理」です。
【命題２】と【命題３】を表面的に言い換えて、まとめたものになります。ですので、証明はすぐに導かれます。
中間値の定理 :中間値の定理の証明
【中間値の定理】
閉区間 [a, b] で連続な関数 f の、この区間における最大値を M、最小値を m とする。
m ≠ M ならば、m < k < M である任意の実数 k に対して、閉区間 [a, b] 内のある点 c が存在し、f(c) = k である。
＜証明＞
閉区間 [a, b] 内の点 d と点 e において、
f(d) = m、f(e) = M とします。
仮定より、m ≠ M だから、d ≠ e です。
[ア] d < e のとき
f は閉区間 [d, e] における連続関数でもあり、
f(d) = m < M = f(e) だから、【命題２】より、閉区間[d, e]内の点 c が存在して、
f(c) = k です。
ここで、閉区間 [d, e] は、閉区間 [a, b] の部分集合だから、点 c は閉区間 [a, b] 内の点です。
よって、結論が示されました。
[イ] d > e のとき
ｆは閉区間 [e, d] における連続関数でもあり、
f(e) = M > m = f(d) だから、
【命題３】より、
閉区間 [e, d] 内の点 c が存在して、
f(c) = k です。
ここで、閉区間 [e, d] は、閉区間 [a, b] の部分集合だから、点 c は閉区間 [a, b] 内の点です。
よって、結論が示されました。【証明完了】
これで、中間値の定理の証明が完成しました。厳密な証明は、複雑ですが、使い方は値域において値がつながっているイメージです。
関連する数学IIIについての記事です。
はさみうちの定理で、三角関数の極限についての有名な式を示しています。
発展内容としてロピタルの定理という記事を投稿しています。
読んで頂き、ありがとうございました。
それでは、今回のブログ記事を終了します。