外直積と内直積 | 群の内直積になるための3条件

2023年2月23日

" 外直積と内直積 “が群として同型になります。

しかし、有限個の部分群が与えられたときに、内直積になるとは限りません。

群が有限個の部分群の内直積になるためには、三つの条件を満たさなければなりません。

内直積の定義と、その同値な書き換えについて、理解をすると、群論の入門内容をより詳しく学習することができます。

なお、二項演算が加法であるときには、有限個数で考えているため、外部直和と内部直和のことです。

外直積と内直積 :外直積の定義

G₁, G₂, … , G_n という有限個の群が与えられたとき、直積集合 G₁ × G₂ × … × G_n に二項演算を定義して、群の外直積を定義することができます。

直積集合であっても、集合なので、二項演算を定義することから始めます。

定義した二項演算について、群の定義を満たすと、その集合と二項演算について群ができ上ります。

次のように、直積集合に二項演算を定義します。

演算の定義

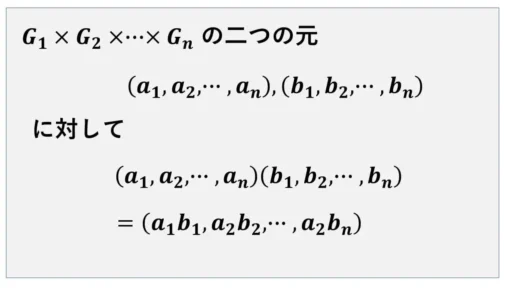
各 i 番目の成分について、G_i において既に定義されている群の積をとるということで、直積集合に積を定義しました。

この二項演算によって、直積集合は群となります。
※ リンク先の記事で、外直積について簡単な例を使って解説をしています。

e_i ∈ Gi を単位元とすると、外直積の単位元は、(e₁, e₂, … , e_n) です。

成分ごとに演算を定義しているので、各直積因子における結合律から、外直積の結合律が導かれます。逆元の存在についても、G_i における逆元の存在から導かれています。

この外直積は、群が n 個与えられれば、いつでも定義することができます。

次に、群 G の有限個の部分群についての内直積の定義を説明します。

この内直積は、部分群なら何でも良いというわけではないので、定義を正確に押さえておくことが必要になります。

外直積と内直積 :内直積の定義

G₁, G₂, … , G_n を群 G の部分群とします。

これらについて、次の (1) と (2) の条件をともに満たすとき、群 G は、G₁, G₂, … , G_n の内直積となっているといいます。

【内直積の定義】

(1) 群 G の各 g に対して、一意的に g_i ∈ G_i が存在して、g = g₁g₂ … g_n と表すことができる。

(2) i ≠ k ならば G_i の各元と G_k の各元は可換である。

さすがに、この定義は部分群が有限個与えられたときに、いつでも満たされるわけではありません。

外直積は、有限個の群が与えられたときに、いつでも定義が可能でした。それに対して、内直積は (1) と (2) の二条件を満たさなければなりません。

この二条件を満たすということは、後で述べる三条件を満たすことが同値になります。

後で述べる三条件を確かめる方が、確かめやすいときが多いです。

その前に、外直積と内直積の関係について説明します。

内直積は外直積と群同型

群 G が、その有限個の部分群 G₁, G₂, … , G_n の内直積となっているとき、G は G₁, G₂, … , G_n の外直積と群として同型である。

＜証明＞

内直積の定義より、群 G の元は、一意的に
g₁g₂ … g_n（g_i ∈ G_i）という形に表されます。

よって、G から外直積への写像 f を次のように定義できます。

f(g₁g₂ … g_n) = (g₁, g₂, … , g_n) です。

内直積の条件 (2) の可換性から、
a_i, b_i ∈ G_i について、

f((a₁a₂ … a_n)(b₁b₂ … b_n))
= f((a₁b₁)(a₂b₂) … (a_nb_n))
= (a₁b₁, a₂b₂, … , a_nb_n)
= (a₁, a₂, … , a_n)(b₁, b₂, … , b_n)
= f((a₁a₂ … a_n))f((b₁b₂ … b_n))

これで、f が準同型写像ということが示せました。

全射性は、(g₁, g₂, … , g_n) を任意の外直積の元だとすると、
各 g_i ∈ G_i ⊂ G なので、
f(g₁g₂ … g_n) = (g₁, g₂, … , g_n) となるからです。

単射性は、ker f = {e} ということから分かります。
※ e は G の単位元です。

外直積 G₁ × G₂ × … × G_n の単位元は、
(e₁, e₂, … , e_n) なので、
g₁g₂ … g_n ∈ ker f とすると、
(g₁, g₂, … , g_n) = (e₁, e₂, … , e_n) です。

直積集合の相当関係（等しい関係）の定義から、成分ごとの値が等しいため、g_i = e_i

群 G の単位元は、どの部分群の単位元とも等しいので、
g₁g₂ … g_n = e₁e₂ … e_n = e

よって、ker f = {e} となり、f は単射であることが示せました。

以上より、f は群同型写像なので、内直積と外直積が群として同型であることが示せました。【証明完了】

これで、内直積と外直積が群として同型になるということが分かりました。

それでは、有限個の部分群が与えられたときに、次の三条件を全て満たせば、群 G がそれらの部分群の内直積となっていることを示します。

外直積と内直積 :内直積の書き換え

【定理】

G₁, G₂, … , G_n を群 G の部分群とする。
次の三条件を全て満たすことと、
G が、G₁, G₂, … , G_n の内直積となっていることは同値である。

[1] G₁, G₂, … , G_n は G の正規部分群
[2] G = <G₁, G₂, … , G_n>
[3] <G₁, G₂, … , G_i> ∩ G_i+1 = {e} （ただし、i は 1 以上 n – 1 の任意の自然数）

＜証明＞

G が G₁, G₂, … , G_n の内直積であるときに、[1], [2], [3] が成立することを先に示します。

任意の a_i ∈ Gi と任意の g ∈ G とします。
g = g₁g₂ … g_n と g_k ∈ G_k を用いて一意的に表され、添え字が異なる部分群の元と元が可換であるという内直積の定義から、

ga_ig^-1 = g₁ … g_na_ig_n^-1 … g₁^-1
= g_ia_ig_i^-1

添え字 i 以外の添え字がついている元は、添え字 i の元と可換なので、逆元と打ち消しが起こります。添え字 i の元だけが残ることになります。

ここで、a_i, g_i ∈ G_i なので、
ga_ig^-1 = g_ia_ig_i^-1 ∈ G

これで、[1] の正規部分群となっているという条件が示せました。

内直積の定義から、群 G の各 g に対して、一意的に g_i ∈ G_i が存在して、

g = g₁g₂ … g_n なので、
G = <G₁, G₂, … , G_n> という条件 [2] も成立しています。
※ <G₁, G₂, … , G_n> は、これらの部分群で生成されているということを示す記号です。

1 ≦ i ≦ n -1 について、
<G₁, G₂, … , G_i> ∩ G_i+1の任意の元を g とします。

g ∈ <G₁, G₂, … , G_i> より、
g = g₁g₂ … g_ie … e,
g₁ ∈ G₁, … , g_i ∈ G_i,
e ∈ G_i+1, … , e ∈ G_n

一方、g ∈ G_i+1 より、
e … ege … e = g

e は G_i 以外の部分群の単位元です。

内直積の表し方の一意性から、
g₁ = g₂ = … = g_n = e

これで、条件 [3] も確認できました。

今度は、逆を確認します。

つまり、[1] と [2] と [3] を全て満たしていれば、群 G が G₁, G₂, … , G_n の内直積となっていることを示します。

逆の証明

まず、i ≠ k のとき、
a_i ∈ G_i と b_k ∈ G_k が可換であることを確認します。

[1] より、G_i と G_k が正規部分群で、
a_ib_ka_i^-1 ∈ G_k, b_ka_i^-1b_k^-1 ∈ G_i だから、
[3] から G_i と G_k の共通部分が単位群なので、
a_ib_ka_i^-1b_k^-1 ∈ G_i ∩ G_k = {e}

よって、a_ib_k = b_ka_i

これで、内直積の異なる添え字の部分群の元が可換であるという条件 (2) が示せました。

今、仮定されている条件 [3] から、
G = G₁G₂ … G_n となっています。

よって、任意の g ∈ G は、
g = g₁g₂ … g_n, (g_i ∈ G_i) と表されます。

そのため、この表し方が、一意的であることを示せば、内直積の条件 (1) が示されたことになります。

g = x₁x₂ … x_n (x_i ∈ G_i) ともなっていたとします。

今、示した異なる添え字の部分群の元と元が可換であることから、
g₁g₂ … g_n = x₁x₂ … x_n なので、
g_nx_n^-1
= (g₁^-1x₁)(g₂^-1x₂) … (g_n-1^-1x_n-1)
∈ <G₁, … , G_n-1>∩G_n = {e}

よって、g_n = x_n

以下、同様にして、
1 ≦ i ≦ n -1 について、
g_i = x_i が、n – 1 から順に従います。

これで、内直積の条件 (1) も示せたので、群 G は、G₁, G₂, … , G_n の内直積となっています。【証明完了】

今回のブログ記事では、外直積と内直積が群として同型ということを示しました。このため、一般に、内直積のことを単に群の直積といったりもします。

ここまでで、内直積が外直積と群として同型になることと、内直積の定義の書き換えについて述べました。これらの内容を総合して、少し練習をしてみます。

外直積と内直積 :群の中心の直積分解

群 G が、G の部分群 H₁, H₂, … , H_n たちの内直積に分解していたとします。

内直積と外直積が群として同型になるので、同一視をして、
G = H₁×H₂×…×H_n と表すことにします。

h_i∈H_i たちについて、
(h₁, h₂, … , h_n) を
h₁h₂…h_n と表します。

このとき、G の中心を Z(G) と表すと、
Z(G) = Z(H₁)×Z(H₂)×…×Z(H_n) となります。

同一視を用いた表し方なので、難しそうですが、内直積の定義から導いています。

試しに、n が 3 のときに確認してみます。

H₁, H₂, H₃ の元たちは、内直積の定義から、添え字が異なれば可換でした。

そのため、h_i∈H_i のとき、
G∋h₁h₂h₃ = h₃h₁h₂ というように添え字が異なっているものたちの積の順番を入れ替えることができます。

そのため、次のような変形をすることができます。

a, x∈G について、内直積の定義から、
a₁, x₁∈H₁, a₂, x₂∈H₂, a₃, x₃∈H₃ を用いて一意的に、
a = a₁a₂a₃, x = x₁x₂x₃ と表せます。

xax^-1 を変形します。添え字が異なると可換という内直積の定義が効いてきます。

xax^-1 = (x₁x₂x₃)(a₁a₂a₃)(x₁x₂x₃)^-1
= (x₁a₁)(x₂x₃)(a₂a₃)(x₃^-1x₂^-1x₁^-1)
= (x₁a₁)(x₂a₂)(x₃a₃)(x₃^-1x₂^-1x₁^-1)

ここで、x_i^-1∈H_i なので、添え字が異なるものの積は可換です。

そのため、
xax^-1 =
(x₁a₁)(x₂a₂)(x₃a₃)(x₁^-1x₂^-1x₃^-1)

x₁^-1 は、添え字が 2 と 3 の元とは可換なので、
xax^-1 =
(x₁a₁x₁^-1)(x₂a₂)(x₃a₃)(x₂^-1x₃^-1)

x₂^-1 は、添え字が 3 の元と可換なので、
xax^-1 =
(x₁a₁x₁^-1)(x₂a₂x₂^-1)(x₃a₃x₃^-1)

このことから、
b∈Z(G) を
b = b₁b₂b₃ (bi∈Hi) と一意的に表すと、
b_i∈Z(H_i) となっています。

実際、h_i∈H_i を任意に取り、
h = h₁h₂h₃ と置くと、
e = hbh^-1
= (h₁b₁h₁^-1)(h₂b₂h₂^-1)(h₃b₃h₃^-1)

h_ib_ih_i^-1∈H_i なので、単位元 e の表し方が一意的であることから、
h_ib_ih_i^-1 = e∈H_i (i = 1, 2, 3) となります。

よって、
Z(G) ⊂ Z(H₁)×Z(H₂)×Z(H₃)

逆に、c_i∈Z(H_i) とし、
c = c₁c₂c₃ と置きます。

任意の y∈G について、内直積の定義から、
y = y₁y₂y₃ (yi∈Hi) と表すと、
ycy^-1 =
(y₁c₁y₁^-1)(y₂c₂y₂^-1)(y₃c₃y₃^-1)

各 i について、c_i∈Z(H_i), y_i∈H_i なので、
H_i∋y_ic_iy_i^-1 = c_iy_iy_i^-1 = c_i です。

ゆえに、
ycy^-1 = c₁c₂c₃ = c となり、
yc = cy です。

c は任意の G の元と可換なので、
c∈Z(G) となり、
Z(G) ⊃ Z(H₁)×Z(H₂)×Z(H₃)

以上を合わせると、
Z(G) = Z(H₁)×Z(H₂)×Z(H₃) となります。

この内容を一般に n を用いて表します。

一般のnについて

G = H₁×H₂×…×H_n のとき、
a, x∈G について、内直積の定義から、
a_i, x_i∈H_i を用いて一意的に、
a = a₁…a_n, x = x₁…x_n と表せます。

(x₁…x_n)^-1
= x_n^-1…x₁^-1 ですが、
内直積の定義から添え字が異なるものが可換になるため、
(x₁…x_n)^-1 = x₁^-1…x_n^-1 となります。

そのため、
xax^-1
= (x₁…x_n)(a₁…a_n)(x₁^-1…x_n^-1)
= (x₁a₁x₁^-1)…(x_na_nx_n^-1)

後は、n = 3 のときと同様に中心に含まれていることを中心の定義に基づいて確かめます。

すると、先ほどと同じく、
Z(G) ⊂ Z(H₁)×Z(H₂)×…×Z(H_n),
Z(G) ⊃ Z(H₁)×Z(H₂)×…×Z(H_n) であることが分かります。

そのため、
Z(G) = Z(H₁)×Z(H₂)×…×Z(H_n) となっています。

添え字が異なる元の積が可換ということを用いて、
xax^-1 = (x₁a₁x₁^-1)…(x_na_nx_n^-1) が決め手になりました。

【関連する記事】

群の作用や置換群が絡む内容の記事になります。

・群の作用（推移的）
・クラインの四元群
・軌道分解

それでは、これで今回のブログ記事を終了します。

読んで頂き、ありがとうございました。