ロルの定理 – 証明|例題で実際に使い効果を実感!
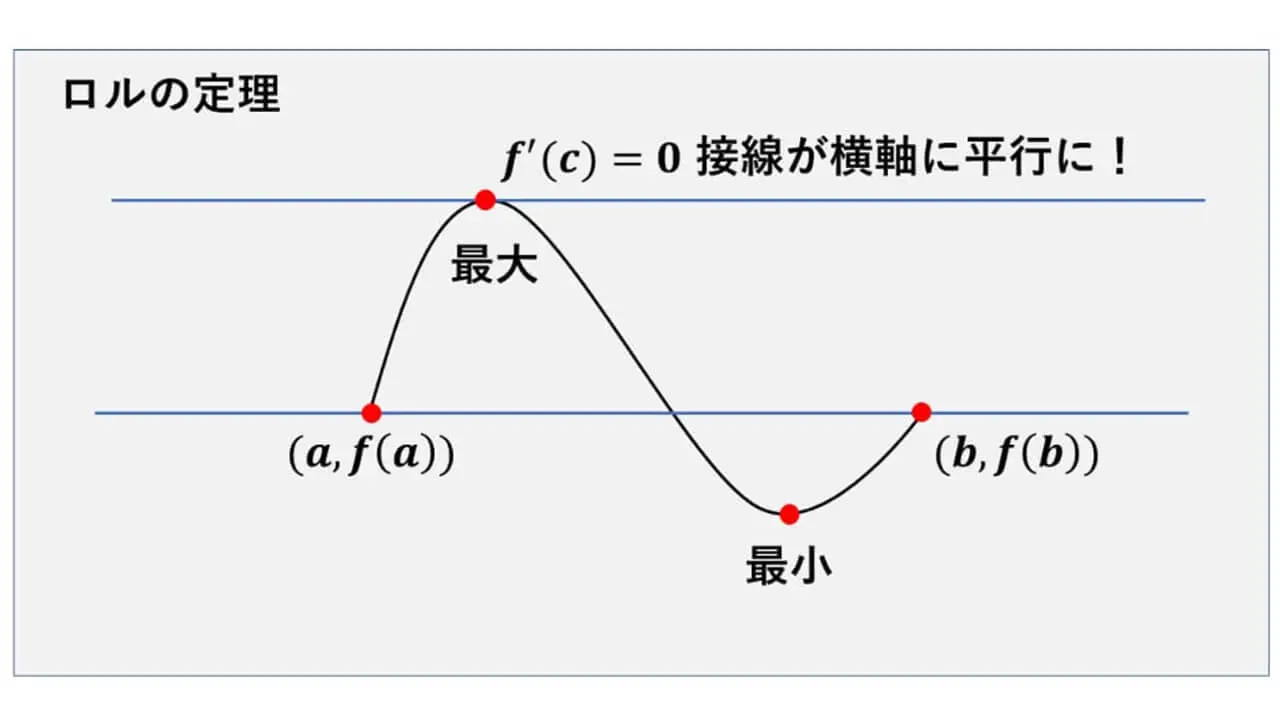
" ロルの定理 “を証明しています。
また、数学3で学習する内容について、ロルの定理を使う例題も述べています。
例題で定理を実際に使ってみると、その定理の効果が実感できます。
証明の際には、次の二点について意識することで、証明の内容が理解しやすくなるかと思います。
・実数 p は、「0 か 0 でないか」のどちらか
・微分可能なら、右極限と左極限が一致する
意識を集中させて証明を理解しようとするときに、力点の置き方を変えると理解がしやすいかと思います。
それでは、ロルの定理の証明へ向けて話を進めます。
ロルの定理 :証明へ向けて
ロルの定理の仮定の一つは、
「a ≦ x ≦ b という範囲を定義域とする連続関数 f(x) について、両端点の値が等しくなっている」ということです。
つまり、f(a) = f(b) となっていることが仮定されているということです。
そして、連続なので、グラフは 1 本の曲線(もしくは直線)です。
グラフを 1 本のロープと思うと、
x の値が a から b へ増加させていったときに、
いきなり +∞ や -∞ になったりしないことが、このイメージから想像できます。
大学の数学では、この部分を厳密に証明します。
閉区間は、閉集合になっていて、この範囲で有界。
そして、有界閉区間上で定義された実数値連続関数は最大値および最小値をとるという連続関数の定理があります。
※ 厳密証明は、リンク先で解説していますが、大学の数学科の内容となっています。
高校の数学では、上の視覚的なイメージをもつことが大切になるかと思います。
※ この視覚イメージを大学数学では、4 次元以上の有界閉集合上で定義された連続関数についての定理へと拡張させます。
証明の流れ
【意識する流れ】
① 有界閉区間 [a, b] における最大値および最小値の定理についての大学数学の引用パート
② f(a) = f(b) の値が、「0 か 0 でないのか」の場合分けと、0 であるときの扱いやすさを実感するパート
③ 微分可能の仮定から、右極限と左極限が同じ実数値に収束することを使うパート
④ 0 でないときの場合の証明を 0 のときの証明に帰着させるパート
ロルの定理の証明は長いので、証明の流れを書いておきます。
次の段階たちを、それぞれの中心となる論点を意識して見て頂けると理解しやすいかと思います。
証明を理解するときに、今、どのパートで議論をしているのかということを意識することで、論点への意識が集中され、理解しやすくなるかと思います。
ロルの定理の証明
【ロルの定理】
実数 a, b が a < b だとする。
関数 f(x) が閉区間 [a, b] で連続、開区間 (a, b) で微分可能とする。
このとき、
f(a) = f(b) ならば、「f'(c) = 0, a < c < b」を満たす実数 c が存在する。
まず、f(a) = f(b) = 0 の場合について結論を導きます。
その後で、f(a) = f(b) の値が 0 でない場合について証明をする流れになります。
【①大学数学で厳密証明をする定理の引用パート】
関数 f(x) は、閉区間 [a, b] で連続です。連続関数の最大・最小値の定理から、a ≦ x ≦ b という定義域について、f(x) は最大値 M と最小値 m をもちます。
※ これで、m ≦ f(x) ≦ M ということが値域において分かりました。
【② f(a) = f(b) の値が 0 を意識するパート】
f(x) の値域が m ≦ f(x) ≦ M なので、もし m = M だとすると、f(x) は定数関数ということになります。
つまり、m も M も f(a) も f(b) もすべて等しいという状況です。
このときは、f(a) = 0 だったので、関数 f(x) の値域は、0 のみということになります。
a < c < b であるどんな実数 c についても、f(c) = 0 となっています。
この定数関数を微分して、
f'(c) = 0 で、定理が成立します。
よって、以下は m ≠ M のときについて議論をしていきます。
m ≠ M という状況では、
m か M のどちらかの値が、
f(a) = f(b) = 0 と異なることになります。
よって、起こり得る場合が、
m ≠ 0 のときと、M ≠ 0 のときとなりました。
M ≠ 0 のときから定理を示すことにします。
a < c < b である実数 c のときに、最大値 M をとるとします。
すなわち、f(c) = M ということです。
M は、関数 f(x) の値域における最大値なので、次のことが成立します。
|Δx| が十分小さいときに、
f(c + Δx) ≦ M = f(c)
よって、
Δy = f(c + Δx) - f(c) ≦ 0 となっています。
中学で学習した変化の割合(平均変化率)の内容で出てくる増加量が登場させることができました。
このとき、次のことが成立します。
【③ 微分可能なので右と左の極限が同じ値に収束するパート】
y = f(x) は開区間 (a, b) で微分可能ということから、
a < x < b である任意の実数 x において、
Δx → 0 としたときに、Δy/Δx は収束します。
Δx > 0 ならば、
Δy = f(c + Δx) - f(c) ≦ 0 の両辺に 1/Δx を掛けると、
Δy/Δx ≦ 0 より、
Δx → +0 としたときの右極限の値は 0 以下となります。
Δx > 0 ならば、1/Δx を掛けたときに不等号の向きが変わり、
Δy/Δx ≧ 0 だから、
Δx → -0 としたときの左極限の値は 0 以上です。
y = f(x) は開区間 (a, b) で微分可能なので、右極限と左極限は一致します。
そのため、Δx → 0 としたときに、
Δy/Δx は 0 に収束することになります。
この収束値が f'(c) で、f'(c) = 0
これで、a < c < b である実数 c について、定理が成立することが示せました。
※ 不等式と極限についての内容を基礎として使いました。
m ≠ 0 のときも同様にして、
f'(c) = 0 が導けます。
a < c < b である c において、
f(c) = m として、
f(c + Δx) ≧ m = f(c) から議論をスタートします。
最大値のときの証明で「≦」と「≧」が逆転するだけで、同じ要領で結論へ到達します。
それだけなので、同様の議論は割愛します。
※ 実数に関連する証明で、この「≦」と「≧」の双対性は、たびたび出てきます。
アイデアは同じで、機械的に「≦」と「≧」を逆転させ、適宜の微調整をするだけのときに、「同様にして」という言い方をよく使います。
これで、f(a) = f(b) = 0 の場合について、証明が完了しました。
証明の最終パートへ
【④ 0 のときの証明に帰着させるパート】
f(a) = f(b) ≠ 0 の場合についての証明を完成させます。
残っているこの証明は、「f(a) = f(b) = 0」の場合に帰着させます。
既に証明した正しい内容を利用するという数学の推論規則の一つです。
f(a) = f(b) の値が 0 でないときは、縦軸方向に平行移動をして、両端点での値が 0 のときにするというわけです。
a ≦ x ≦ b である実数 x について、
g(x) = f(x) - f(a) と新しい関数を定義します。
この関数 g(x) は、閉区間 [a, b] で連続、開区間 (a, b) で微分可能です。
そして、g(a) = 0 です。
さらに、g(b) = f(b) - f(a) ですが、f(a) = f(b) なので、g(b) = 0 となっています。
これで、g(a) = g(b) = 0 となっています。
これで、先ほど証明した内容のスタート地点にこれました。
上で書いた証明の関数 f(x) を関数 g(x) に書き換えて同じ議論をすると、
g'(c) = 0, a < c < b を満たす実数 c が存在します。
g(x) = f(x) - f(a) で、f(a) は定数なので、両辺を x で微分すると、
g'(x) = f'(x)
つまり、f'(c) = g'(c) = 0
これで、証明したい定理の結論へ辿り着けました。【証明完了】
ここからは、示したロルの定理を使う例題について述べます。
ロルの定理 :例題
三次関数 f(x) = x3-4x は、
閉区間 [0, 2] で連続で、
開区間 (0, 2) で微分可能です。
さらに、f(0) = f(2) となっています。
このため、ロルの定理から、
f'(c) = 0, 0 < c < 2 を満たす実数 c が存在します。
f(x) = x3-4x だと、実際に微分を計算して、c の値を求めることができます。
f'(x) = 3x2-4 です。
f'(x) = 0 を満たす実数は、
3x2-4 = 0 という二次方程式の解です。
この判別式は、
02-4・3・(-4) > 0 なので、
二次方程式は異なる二つの実数解をもちます。
しかし、今、0 < c < 2 という条件も満たす実数を考えているので、
3x2-4 = 0 の実数解のうち、0 より大きくて 2 より小さい範囲に入っている実数を c とします。
ロルの定理の結論の実数の範囲を示す不等式にも注意です。
もう1つ例題です。
今度は計算が複雑になります。
もう1つ例題
f(t) = t1/3(1-t) について、
f'(c) = 0, 0 < c < 1 を満たす実数 c を求めてください。
f(t) は閉区間【0, 1】で連続で、開区間 (0, 1) で微分可能です。
そのため、ロルの定理から、
f'(c) = 0, 0 < c < 1 を満たす実数 c が存在することが分かります。
この c の値を求めるという内容になります。
ここからは、0 < t < 1 という範囲で議論をします。
f'(t) = 1/3×t-2/3(1-t)-x1/3 です。
0 < t < 1 の範囲なので、t-2/3 は 0 でないため、分母に置くことができます。
c の値を具体的に求めるために、f'(t) を通分を使って見やすい形にします。

0 < t < 1 の範囲で、
f'(t) = 0 とすると、t2/3を両辺に掛けることで、分子の値が 0 となっていなければならないことが分かります。
つまり、1-4t = 0 です。
これは、t = 1/4 ということです。
逆に c = 1/4 は、0 < c < 1 で、
f'(c) = f'(1/4)
= 0/3t2/3 = 0 となっています。
よって、この 1/4 が求める値です。
このような分数指数の計算をすることが、数3の計算では多いです。
※ リンク先の記事では数式の入力コードについて説明をしています。
他の定理への広がりについて
この記事で示したロルの定理から、平均値の定理(ラグランジュの平均値の定理)が導かれます。
平均値の定理は、数学では二つあります。
ラグランジュとコーシーの定理です。
ラグランジュの平均値の定理は関数の増減表の根本的な拠り所となります。
つまり、関数の増加と減少を一次導関数を用いることで判断できるための根拠になります。
そして、ラグランジュの平均値の定理からコーシーの平均値の定理が導かれ、コーシーの平均値の定理を使ってロピタルの定理が導かれます。
ロピタルの定理は、高校の範囲外ですが、不定形の極限が出てきたときに、分子と分母を微分すると極限が求められるので、知っておくのも良いかと思います。
※ただ、大学受験の記述問題では、学習外の内容なので答案に書かずに、求めた極限の見直しなどに使うと良いかと思います。
大学へ入学した後の数学では、普通に使います。
【関連する数3記事】
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。