群数列 – 解き方 |第k群の項数を決めるパターン規則【数B】

2023年11月25日

" 群数列 – 解き方 “について、はじめに与えられた数列の項の値たちを集めて区切る仕組みについて解説しています。

第1群、第2群と順に区切る仕組み（パターン）を捉えることができると、群数列が扱いやすくなります。

第k群の最初の数や終わりの数を求めるためには、この区切る仕組みの理解が大切になります。

基本となる仕組みに関わるのは、関数（数列）の対応です。

第k群の k という自然数に対して、対応する項数の数を押さえることで、群数列というものへの理解が深まるかと思います。

では、与えられた数列の項たちを、どのようにして区切るかということについて説明します。

群数列 – 解き方 | 各群を区切る仕組み

{a_n} : 1, 2, 3, 4, …

この初項（第1項）が 1 で、交差 1 の等差数列を、はじめに与えられた材料として、ここから群数列を作ります。

群数列を定義するためには、どのような仕組みで群れという集合を作るのかということを決めます。

この群れたちを区切る決まりとして、関数（数列）f(k) を定義します。

感覚的に捉えられることが多い第k群に含まれる項の数ですが、これを関数（数列）f(k) として積極的に意識した述べ方を、この記事ではするようにします。

このステップで、はじめに与えられた数列から、群数列を作ります。

では、具体的に群数列を作ってみます。

関数f(k)を設定する

各自然数 k に対して、
f(k) = 2^k-1 と設定してみます。

k = 1 のとき、
f(1) = 2⁰ = 1 なので、第 1 群の項数は 1 個です。

{a_n} : 1, 2, 3, 4, … だったので、
{a₁} = {1} という 1 個だけの要素から成る集合が第 1 群となります。

k = 2 のとき、
f(2) = 2¹ = 2 なので、第 2 群の項数は 2 個です。

第 1 群から順に項数に応じた個数の数を、はじめに与えられた数列からとるというステップを踏みます。

取る 2 個は第 1 群に含まれる最後の a₁ の次の添え字から数えて二つです。

つまり、a₂, a₃ が第 2 群に含まれる 2 個の値となります。

{a₂, a₃} = {2, 3} が第 2 群です。

ここまでの群れによる区切りをまとめておきます。

a₁ | a₂, a₃| , …

はじめに与えられた数列の一般項である第 n 群の値を文字 n を用いて表せていると、a₂ などの値を具体的に計算で求めることができます。

数列 {an} は初項 1 で、交差が 1 の等差数列だったので、
a_n = n です。

そのため、第 2 群は、
{a₂, a₃} = {2, 3} となります。

はじめに与えられた数列の規則は、それぞれの群れに含まれている要素の値と連動します。

この連動を利用するためには、添え字の値が明確になっていなければなりません。

a₃ だと、はじめに与えられた数列の第 3 項の値と分かります。

このように、添え字が 3 ということは、はじめの数列の第 3 項の値ということなので、添え字を通じて対応を適宜、考えることができます。

もう少し、それぞれの群れに含まれている要素を調べる練習をします。

第k群の末と第(k+1)群のはじめ

今度は、第 3 群に含まれている要素たちを書き出します。

k = 3 なので、関数 f を使って、含まれる要素の個数を求めます。

f(3) = 2^3-1 = 2² = 4 です。

このため、第 3 群には、4 個の値が含まれることになります。

第 2 群は、{a₂, a₃} でした。

第 2 群の末は a₃ なので、第 3 群のはじめは a₄ からスタートします。

4 個の値が含まれるので、
a₄, a₅, a₆, a₇ の 4 個が第 3 群に含まれる値たちです。

一般に、
第 k 群の末の項の添え字より、
第 k+1 群のはじめの項の添え字の方が 1 だけ大きいです。

この当たり前といえば当たり前のことですが、正確に添え字を押さえるときに、役立つ重要な情報となります。

より実践的に、第 k 群の末の項の添え字の値を計算する方法を述べておきます。

第 3 群 は、
{a₄, a₅, a₆, a₇} でした。

どうして、末の項が a₇ かというと、
f(1)+f(2)+f(3)
= 1+2+4 = 7 だからです。

このため、第 3 群の末の項の添え字が 7 です。

各群れに含まれる項数を定めていた関数 f と、群れの末の項の添え字の対応関係になります。

対応関係を練習するために、第 4 群の末の項の添え字を調べてみます。

群数列 : 第k群の末の項の添え字

【よく使う情報】

第 k 群の末の項の添え字は、
f(1)+f(2)+…+f(k) である。

厳密な証明をすると数学的帰納法ですが、直観通りに明らかなので、具体例で様子を確認することに留めておきます。

f(k) = 2^k-1 でした。

そのため、
f(1)+f(2)+f(3)+f(4)
= 1+2+4+8
= 15 です。

そのため、15 が第 4 群の末の項の添え字となります。

では、実際に確かめてみます。

第 3 群は、
{a₄, a₅, a₆, a₇} でした。

f(4) = 2^4-1 = 8 なので、
a₈ からスタートして、8 個の値たちを並べることになります。

a₈, a₉, a₁₀, a₁₁,
a₁₂, a₁₃, a₁₄, a₁₅ の 8 個が、第 4 群に含まれる 8 個の項たちです。

第 3 群の末の項が a₇ で、
f(4) = 8 です。

a_7+f(4) = a₇₊₈ = a₁₅ が第 4 群の末の項。

これが、ドミノ倒しの仕組みです。

添え字の動きをシグマで追跡

第 k 群の末の項の添え字は、
f(1)+f(2)+…+f(k) である。

すなわち、
Σ_i f(i) で i は 1 から k まで走る。

第 4 項の末の項の添え字くらいだと、第 1 群から順に書き出すと分かるかもしれませんが、より一般的にシグマを使って述べておきます。

シグマで捉えておくと、
シグマ記号の公式を使って、具体的に計算をすることができます。

試しに、第 6 群の末の項の添え字を計算で求めます。

さすがに、すべて書き出すのは困難です。

しかし、シグマの公式が手助けをしてくれます。

f(k) = 2^k-1 でした。

第 6 群の末の項の添え字は、
f(1)+f(2)+…+f(6) となります。

f(k) が文字 k を使って表されている状態なので、シグマの公式が使えます。

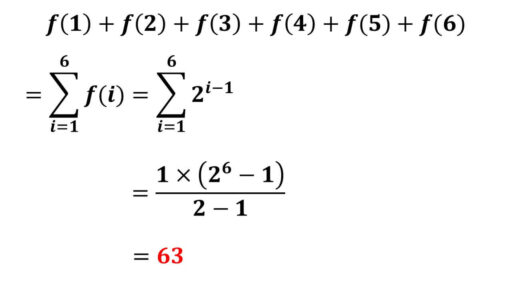
故に、第 6 群の末の項の添え字は 63 です。

f(k) = 2^k-1 というように、
第 k 群に含まれる項数を k を用いて表せているときは、シグマ記号の公式を使って計算できるときもあります。

※ もちろん、k を使った式が、シグマ記号の公式に無い複雑なものだと、他のアプローチを考えるわけですが、そういった難問の類いは置いておいて、まずは基礎的な内容で練習をすると良いかと思います。

ちなみに、同じ流れで、
第 k+1 群のはじめの項の添え字もシグマ記号を使って表すことができます。

f(1)+f(2)+…+f(k)+1
= Σ_i f(i) + 1 です。

では、ここまでの内容を使って、大きな数について理論を使って推論を進める練習をします。

群数列 :理論の適用

{a_n} : 1, 2, 3, 4, …
第 k 群の項数は f(k) = 2^k-1 です。

このとき、500 という、もとの数列がとる値が、第何群の何番目の項になるのかを求めてください。

a_n = n が、もとの数列の一般項です。

そのため、500 は、
もとの数列の 第500項の値です。

つまり、a₅₀₀ = 500 です。

先ほどの考え方から、
第 k 群の末の項の添え字は、
f(1)+f(2)+…+f(k)
= (2^k－1)÷(2－1)
= 2^k－1 です。

k に具体的な自然数を代入して様子を確認しつつ、最後の詰めを論理的に行います。

2の10乗は1024

2¹⁰ = 1024 は知っておくと目安にできるので役立ちます。

そのため、
2⁹－1= 1024÷2－1 = 511,
2⁸－1= 512÷2－1 = 255 です。

255 が第 8 群の末の項の添え字です。

そして、511 が第 9 群の末の項の添え字です。

これで、a₅₀₀ = 500 が、
第 9 群に含まれていることが分かりました。

{a₂₅₆, … , a₅₁₁} が第 9 群です。

この中に a₅₀₀ が居ます！

a₂₅₆ が第 9 群の 1 番目の項です。

ここからが最後の詰めです。

ドミノ倒しで推論

a₂₅₆₊₁ = a₂₅₇ が (1+1) 番目です。

a₂₅₆₊₂ = a₂₅₈ が (1+2) 番目です。

一般に、
a_256+m が (1+m) 番目です。
（ただし、m ≦ 255）

厳密には帰納法ですが、直観的に明らかなので、認めて議論を進めます。

256+m = 500 となるのは、
m = 244 のときです。

中学数学からの方程式の考え方が役に立ちました。

a_256+m が (1+m) 番目で、
m = 244 のときより、
a₅₀₀ は (1+244) 番目です。

すなわち、a₅₀₀ は、
第 9 群の 245 番目の項です。

帰納法の考え方から、最後の防壁が崩れました。

答えが求まりましたが、ドミノ倒しの部分を数学的帰納法で示しておきます。

a₂₅₆₊₁ = a₂₅₇ が (1+1) 番目でした。

そのため、m = 1 のとき成立しています。

m = i のとき、
a_256+i が (1+i) 番目だと仮定します。
（ただし、i ≦ 254）

すると、
a_256+i+1 が {1+(i+1)} 番目です。

よって、m = i+1 のときにも成立しています。

このように、数学的帰納法から、
a_256+m が (1+m) 番目の項ということになります。

群数列の問題は、添え字の動きを正確に追うことが大切になります。

理論を適切に使うことと、推論に関しては帰納法を合わせて使います。

ただ、上で述べたように、帰納法の部分は証明を書くと明らかなケースがほとんどなので、厳密な証明を述べなくて良いレベルのものが多いかと思います。

しかし、正確に添え字が違っていないかどうかを押さえるためにも、ドミノ倒しの考え方に慣れておくことが重要になります。

群数列の練習問題:数B

＜解説と解答＞

まず自然数 k に対して、第k群がどうなっているのかを一般的な形で捉えます。

分母が同じ数の分数たちで１つの群が形成されています。

k/k+2, k-1/k+2 と順に k 個の項が続き、右に１つずれると分子の数が１減るという規則（パターン）です。

そして 1/k+2 が第k群の最後の項となります。

つまり、
k/k+2, k-1/k+2, … , 1/k+2 という k 個の項で第k群が形成されています。

次に11/15 が第何群に含まれているのかを考えます。

分母の 15 から決定します。

k+2 = 15 となるのは、
k = 13 のときです。

したがって、
11/15 は第13群に含まれていることになります。

群を形成している規則から、
13/15 が第13群の先頭の項となります。

そのため、13/15, 12/15, 11/15 という数の並びとなります。

これで、11/15 が第13群の3番目の項ということが分かりました。

もとの数列の何番目か

この練習問題は、11/15 が、もとの数列において第何番目の項かということでした。

第k群には k 個の項が含まれているということから、計算して求めます。

第1群から第12群までに含まれている項の数の合計に 3 を加えます。

それが、11/15 のもとの数列において第何番目の項かということを示す数字となります。

つまり、
(1+2+…+12)+3 の値を求めれば良いということになります。

等差の和の公式を使うと値を計算することができます。

(1+2+…+12)+3
= 1/2×(1+12)×12+3
= 78+3
= 81 が求める値となります。

すなわち、
11/15 は第81番目の項ということになります。

関連する数列単元の記事として、次のような記事も投稿しています。

■ 等比数列の和

数列単元を学習するときに、はじめの方で出てくる内容で、その後も頻繁に使うので導き方から理解をしておくと良いかと思います。

■ フィボナッチ数列

これは、漸化式についての内容になります。

漸化式で、ドミノ倒しの要領で初期値から順に数列の項の値が決まるという内容の良い例となる数列です。

■ 一次分数型の漸化式

こちらも、ドミノ倒しの考え方が背後に関わる漸化式の内容になります。

どちらも特性方程式が複雑なタイプで発展的ですが、余裕があるときにチャレンジしておくとためになるかと思います。

また、数II の対数分野についての記事も投稿しています。

真数と底について、定義に基づいて基礎となる式の書き換えについて解説をしています。

それでは、これで今回の記事を終了します。

読んで頂き、ありがとうございました。