連続整数の積 | n個の連続する整数をすべて掛けるとn!の倍数

" 連続整数の積 " について、n 個の連続する整数をすべて掛け合わせると n! の倍数となるということを証明します(この n は自然数です)。
この証明をするにあたって、自分で関数(写像)を定義すると、証明がしやすいです。
結果を導き出す過程に注目して、正確な証明をする良い練習になる命題かと思います。
今回のブログ記事では、場合の数や確率の単元でお馴染みの n! を使います。
※ 目次の項目を選択すると該当箇所へ移動します。
連続整数の積 :記号の説明から
自然数 n について、n!(n の階乗)は、次のように 1 から n までの自然数を掛け合わせ値となっています。
1 × 2 × … × (n – 1) × n が n の階乗です。
このブログで証明する内容は、連続する n 個の整数の積が、必ず n! の倍数となっているということです。
具体的な例で、証明しようとしている内容を見てみます。
5 × 6 × 7 × 8 だと、連続する 4 個の整数(自然数)の積です。
この値が 4! で割り切れるということを確かめてみます。
1680 が、これら 4 個の整数の積です。
4! を階乗の定義に基づいて計算をすると、
1 × 2 × 3 × 4 = 24 となります。
1680 ÷ 24 = 70 なので、確かに 4! の倍数となっています。
この内容を一般の n という自然数を用いて証明をします。
この証明で、数学的帰納法を使います。連続する n 個の整数が与えられると、それらをすべて掛け合わせた値が定まるので、関数(写像)を定義します。
そうすると、証明の計算がスムーズにできます。
整数というと、0 や負の整数もあるので、場合分けをして議論を進めます。
「連続する n 個の整数がすべて自然数の場合」、
「n 個の中に 0 が含まれる場合」、
「n 個がすべて負の整数である場合」という三つの場合に分かれます。
まずは、すべて自然数の場合について証明をします。
この場合について証明しておくと、それを用いて他の場合も証明ができます。
すべて自然数の場合
【命題 1】
n を自然数とする。
自然数 t から自然数 (t + n – 1) までの連続する n 個の自然数の積は、n! の倍数である。
<証明>
n = 1 のときは、1! = 1 はどんな整数も割り切るので、命題が成立しています。
n = k のとき、命題が成立していると仮定して、
n = k + 1 のときにも命題が成立することを示します。
t × (t + 1) × … × (t + m -1) という t から始める連続する m 個の自然数の積を fm(t) と置くことにします。
t から始める (k + 1) 個の連続する自然数の積は fk+1(t) です。
t から始まる (k + 1) 個の連続する自然数の積は fk+1(t + 1) です。
m が k + 1 のときを考えているので、
fk+1(t + 1)
= (t + 1)(t + 1 + 1) … (t + 1 + k)
= (t + 1)(t + 2) … (t + k + 1) となっています。
fk(t) = t(t + 1) … (t + k) です。
次に、
fk+1(t + 1) – fk+1(t) を計算すると、
fk+1(t + 1)
= (t+1)(t+2) … (t+k)(t+k+1),
fk+1(t) = t(t+1) … (t+k-1)(t+k) より、
fk+1(t + 1) – fk(t)
= (t+1) … (t+k){(t+k+1) – t}
= (t+1) … (t+k)(k+1)
(t + 1) … (t + k) は連続する k 個の自然数の積なので、帰納法の仮定から、k! の倍数となっています。
そのため、この部分を k! × s (s は自然数) と表せます。
よって、
fk+1(t + 1) – fk+1(t)
= k! × s × (k + 1) = s(k + 1)!
※ k!(k + 1) = (k + 1)!
t を任意の自然数として、ここまでの議論が成立します。
そのため、t としてどんな自然数を考えても、
fk+1(t + 1) – fk+1(t) が (k + 1)! の倍数となっています。
そこで、t – 1, t – 2, … , 2. 1 を t に代入して、それらの式をすべて足し合わせます。
階差数列で学習したときの要領です。
{fk+1(t)-fk+1(t -1)}
+{fk+1(t-1)-fk+1(t-2)}
+ … + {fk+1(2)-fk+1(1)}
= fk+1(t) – fk+1(1)
fk+1(1) を移項すると、
{fk+1(t)-fk+1(t -1)}
+{fk+1(t-1)-fk+1(t-2)}
+ … + {fk+1(2) – fk+1(1)} + fk+1(1)
= fk+1(t)
ここで、先ほど述べたように、
各 fk+1(i) – fk+1(i – 1) は (k + 1)! の倍数です。
そのため、
fk+1(1) が (k + 1)! の倍数であることを示せば、
fk+1(t) が (k + 1)! の倍数ということが示せたことになります。
fk+1(1) = 1 × (1 + 1) × … × k(k + 1)
なので、fk+1(1) = (k + 1)!
このため、fk+1(1) は (k + 1)! の倍数です。
よって、fk+1(t) が (k + 1)! の倍数であることが示せました。
以上より、数学的帰納法から、
どんな自然数 n についても命題が成立していることが示せました。【証明完了】
次に、連続する n 個の整数の中に 0 が含まれている場合から議論を続けます。
連続整数の積 :残りの場合について
自然数 n について、連続する n 個の整数を
a1, a2, … , an とします。
この中に、0 が現れていると、
a1 × a2 … × an = 0
0 は n! で割り切れるので、 0 は n! の倍数です。
よって、連続する n 個の整数の中に 0 が現れるときは、n! の倍数となります。
※ この場合は、(-2)(-1)×0×1×2 = 0 というような場合です。
積が 0 になるのは、最も明らかな場合ですが、すべての場合をきっちりと示すために、文字を使って正確に述べました。
これで、残った場合は、連続する n 個の整数がすべて負の整数の場合だけです。
この場合を証明すると、目指していたことが証明できたことになります。
すべて負の整数の場合
【命題 2】
n を自然数とする。
a1, a2, … , an を連続する n 個の負の整数とする。
このとき、a1a2 … an は n! の倍数である。
<証明>
1 以上 n 以下の各 i について、
ai < 0 なので、-ai は自然数です。
( – a1), … , ( – an) は連続する n 個の自然数なので、【命題 1】から n! の倍数となっています。
そのため、
( – a1)( – a2) … ( – an) = n! × s
(ここで s は整数)と表すことができます。
両辺に ( – 1)n を掛けると、
a1a2 … an
= n! × {( -1)n × s}
これは a1a2 … an が n! の倍数であることを示しています。【証明完了】
三つの場合に分けて証明をした内容をまとめておきます。
まとめ
【定理】
n を自然数とする。
連続する n 個の整数の積は n! の倍数である。
例えば、(-13)×(-12)×(-11) だと、
13×12×11×( -1)3 が 3! の倍数ということを表している定理です。
本質は【命題 1】で、残りの場合は、ちょっとした工夫で即座に導かれるものです。
文字を使った一般的な証明は、難しそうな雰囲気がありますが、単純な内容のときもあります。
この【定理】を使って、ちょっとした証明問題を考えてみます。
連続整数の積 :練習問題
【練習問題1】
整数 n について、
n(n+1)(2n+1) が 6 の倍数であることを証明してください。
<証明>
n(n + 1)(2n + 1) =
n(n + 1){(n + 2) + (n – 1)}
= n(n + 1)(n + 2) + (n – 1)n(n + 1)
n(n + 1)(n + 2) は連続する 3 個の整数なので、【定理】より、3! 、つまり 6 の倍数です。
(n – 1)n(n + 1) も連続する 3 個の整数なので、同様に、6 の倍数です。
6 の倍数と 6 の倍数の和は 6 の倍数なので、
n(n + 1)(2n + 1) は 6 の倍数 となっています。【証明完了】
このように、連続するn個の整数の積が n! の倍数となっていることを利用した証明問題は、高校数学で頻出の問題となります。
もう1つ練習問題です。
さらに練習
【練習問題2】
z を整数とするとき、
z7-z が 7 の倍数であることを証明してください。
<証明>
z7-z = z(z6-1) です。
z6-1 は先ほど因数分解しています。
z7-z = z(z6-1) =
z(z+1)(z2-z+1)(z-1)(z2+z+1)
… ★
結論は、7 の倍数ということなので、7 に整数を掛けた形へと式を書き換えたいところです。
(z-1), z, (z+1) と、よく見ると連続する整数の積が現れています。
ただ、これだけだと 3! で、肝心の 7 が見えません。
ここで、工夫をします。
★に現れている式で、
z2-z+1, z2+z+1 に改良の余地がありそうです。
公立の中学で学習する展開や因数分解の練習で出てきそうな式ですが、微妙に因数分解の公式に当てはまらない形です。
(z+1)(z-2) = z2-z-2
だったら、さらに因数分解ができるという状況ですが、微妙に係数が当てはまりません。
そういえば、
(z-1), z, (z+1) と、連続する整数の積がありました。
3! だと 7 が無い。7! だと 7 が現れる。
ここで、あきらめないで工夫した式の書き換えを考えます。
7 個の整数の連続した積にするためには、
z+1 より 1 だけ大きい z+2 が切望されます。
z+2 を使う形で、試してみます。
(z+2)(z-3) = z2-z-6
この式は、
z2-z+1 よりも 7 だけ小さくなっています。
定数項の値の違いは、加法や減法で調整することができます。
つまり、
z2-z+1 = (z2-z-6)+7
= (z+2)(z-3)+7 です。
分配法則で展開したときに 7 が掛けられるので、7 の倍数が出現することになります。
ただ、連続する 7 個の整数には、まだ 2 個だけ遠い状況です。
ここまでで、
z-3, z-1, z,
z+1, z+2 という 5 個の整数が連続しそうです。
そこで、z2+z+1 にも同じ発想で、連続した 7 個の整数になる因数を作ることを試みます。
z-2 が欠落している状況なので、この式を使う形での書き換えを考えます。
(z-2)(z+3) = z2+z-6
この式は、z2+z+1 よりも 7 だけ小さくなっています。
そこで、
z2+z+1 = (z2+z-6)+7
= (z-2)(z+3)+7 です。
これで、
z-3, z-2, z-1,
z, z+1, z+2, z+3 という 7 個の連続した整数が現れました。
★の式を書き換えて、結論を目指します。
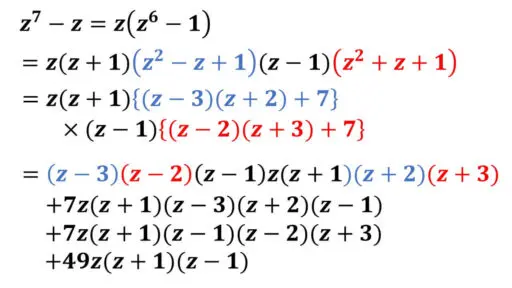
(z-3)(z-2)(z-1)z(z+1)(z+2)(z+3) は、連続する 7 個の整数の積です。
そのため、7! の倍数となっています。
そのため、この部分を、ある整数 a を用いて、
(7!) × a と表すことができます。
また、
7z(z+1)(z-3)(z+2)(z-1)
+7z(z+1)(z-1)(z-2)(z+3)
+49z(z+1)(z-1) は 7 の倍数です。
この部分を、ある整数 b を用いて、
7b と置きます。
すると、★より、
z7-z = (7!) × a + 7b
= 7(6! × a+ b) となります。
6! × a+ b は整数なので、
z7-z は 7 の倍数です。【証明完了】
式の展開や因数分解と合わせて、定数項の部分を加法や減法で調整するという発想も持っておくと、結論に適した形への書き換えが浮かぶときもあるという問題でした。
【整数の記事】
倍数となっているということは、割り切れるということです。
余り-整数問題というブログ記事では、割り切れないときに余りが等しいのか、等しくないのかということを判断するための効果的な命題を取り挙げています。
高校数学の難しい証明問題のような部分もありますが、大学の数学にもつながる内容となっています。
割り切れるときと、割り切れないときのどちらについても理解を深めておくと良いかと思います。
それでは、これで今回のブログ記事を終了します。読んで頂き、ありがとうございました。