線型空間の公理 | 零元はただ1つなど簡単に導けるものも証明
線型空間の公理 (定義)から、大学数学で線形代数学を学習するときに、集合の考え方が基本の1つとなります。
公理は定義と思っておくと気分が楽かと思います。
この記事では、公理からすぐに導けるものとして、零元がただ1つのみであることを示しています。
線型空間の公理に、体が使われています。
ややこしそうだと思ったら、高校の数学でベクトルをスカラー倍していた実数全体だと思ってください。
線型空間の公理 ;体や集合の内容も使用
線型空間のことを線形代数やベクトル空間ともいいます。
いずれにしても、表している内容は同じです。
公理には体 (field) が使われます。
体は加法と乗法が定義されていて、線型空間にスカラー倍という作用をします。
Kは体という四則演算が可能なものです。
線型空間は、加法という二項演算が定義されていて、体からのスカラー倍も定義されています。
【線型空間の公理(定義)】
空集合ではない集合Vが線型空間であるとは、次を満たすことです。
①和という二項演算が定義されている
V×V → V という写像(関数)のことを二項演算と呼びます。
( x , y ) に対して x+y というVの要素(元)を対応させる写像の対応規則が与えられています。
②スカラー倍が定義されている
K×V → V という写像(関数)のことをスカラー倍といいます。
( k, x ) に対して kx というVの要素(元)を対応させる写像の対応規則が与えられています。
これらの演算について、次の③から⑦が成立します。
③加法の結合法則
(x+y)+z = x+(y+z)
④加法の交換法則 x+y = y+x
⑤零元の存在
0∈Vが存在して、
どんな x∈Vに対しても 0+x = x
⑥逆元の存在
Vの各要素(元)xに対して,
a∈Vが存在し、x+a = 0
⑦次のように加法とスカラー倍が関係
k(x+y)=kx+ky
(k∈K, x, y∈V) ,
(a + b)x = ax + bx
(a,b∈K, x∈V),
(ab)x = a(bx) (a,b∈K, x∈V),
1x =x
(1はKの積に関する単位元で x∈V)
これら①から⑦の線型空間の公理を満たすものを線型空間といいます。
また、線型空間の各要素(元)のことをベクトルといいます。
たくさんの条件がありますが、定義です。
これらに当てはまるかどうかとシンプルに思っておくと心理的な負担が軽くて良いかと思います。
具体例
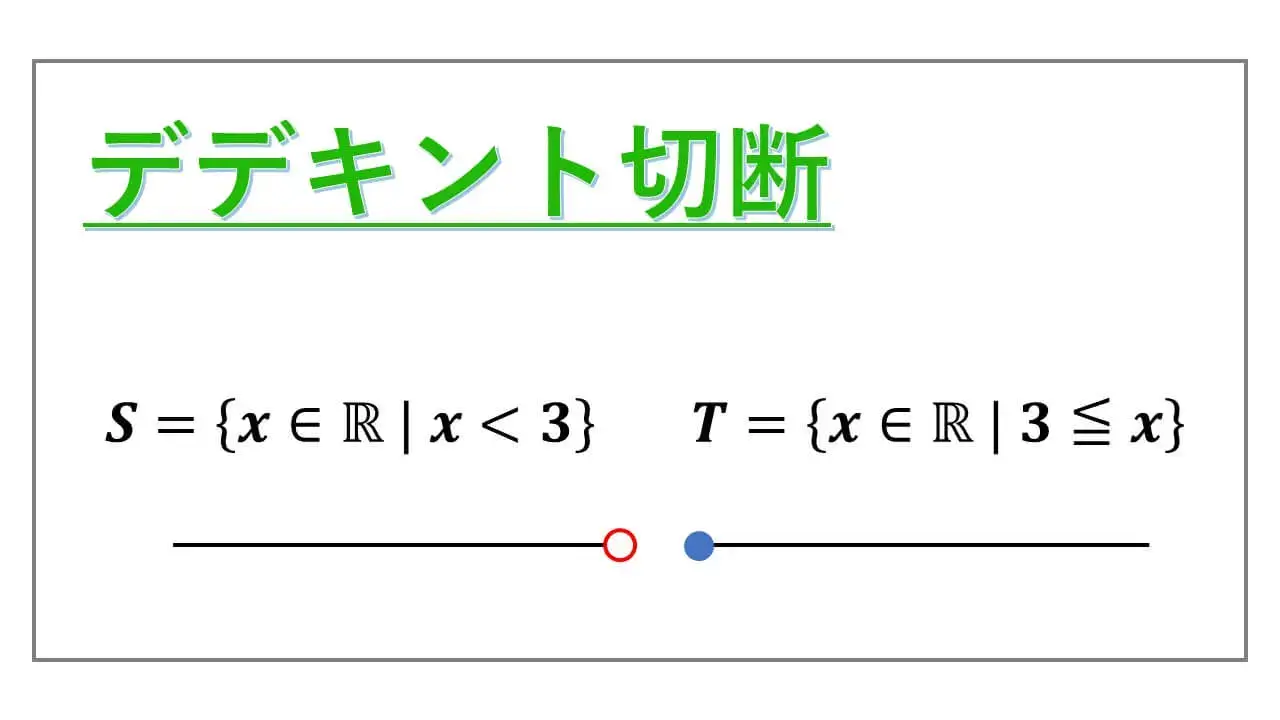
R は実数全体から成る集合です。
R × R ={(a, b) | a, b∈R} は線型空間です。
この R × R は、中学数学で学習した xy 座標平面です。
そして、ベクトルの加法とスカラー倍を高校数学で学習します。
(a, b) + (c, d) = (a + c, b + d) でした。
これが、R × R における加法です。
そして、スカラー倍は、
k(a, b) = (ka, kb)
このように、加法とスカラー倍を定義すると、
R × R は、実数体 R 上の線型空間の公理(定義)に当てはまります。
このスカラー倍に関わってくるものが体です。
体の定義について
線形代数学を学習し始めたときは、四則演算ができて、ベクトル空間へスカラー倍という作用をするものと思っておけば十分です。
※ 体の公理(定義)については、直積集合という記事で述べています。
ちなみに、スカラー倍ですが、正確には次のような直積 K × V から V への対応で、線型空間の公理の条件を満たすものになります。
K × V → V で、(k, v) ∈ V に対して、
kv ∈ V を対応させています。
この対応で、線型空間の公理に書いてある条件をすべて満たすものということです。
個々の線型空間について、このスカラー倍の定義は様々です。
線型空間の公理 :定義から導かれる内容
線型空間の公理から、すぐに導ける内容で、よく使われるものを証明しておきます。
以下において、体 K 上の線型空間 V として議論を進めます。
体 K の元のことをスカラーと呼びます。
線型空間の零元を 0V と表し、体 K の零 0K と区別をして認識することに慣れることが理解の近道となります。
零元とスカラー倍で証明すべきこと[1]
【命題1】
k ∈ K, 0V ∈ V について、
k0V = 0V
<証明>
0V = 0V + 0V なので、両辺を k ∈ K でスカラー倍をしたときの値は同じになります。
よって、k0V = k(0V + 0V)
この右辺にベクトル空間の公理⑦を適用すると、
k0V = k0V + k0V
左辺と右辺は、線型空間 V の元として等しいので、-k0V と加法を計算した結果は、左と右で同じ元です。
ゆえに、
-k0V + k0V
= (-k0V + k0V) + k0V
ここで、加法についての逆元の定義である公理⑥から、
-k0V +k0V = 0V
※公理では、a と逆元のことを書いていますが、実際は前に「-」をつけて、加法に関する逆元を表します。
ゆえに、0V = 0V + k0V
さらに零元の定義である公理⑤を右辺に適用すると、
零元と加法をとっても値が変わらないので、
0V = k0V 【証明完了】
証明すべきこと[2]
【命題2】
0K ∈ K, v ∈ V に対し、
0Kv = 0V
<証明>
0K = 0K + 0K なので、
0Kv =(0K + 0K)v = 0Kv + 0Kv
左辺と右辺に、-0Kv を加えると、
-0Kv + 0Kv
= (-0Kv + 0Kv) + 0Kv
よって、左辺の値は 0V となるので、
0V = 0V + 0Kv = 0Kv【証明完了】
もう一つ、基本となる内容を証明しておきます。
零元の存在は、線型空間の公理によって保証されていますが、その零元は、1つの線型空間に1つしか無いという内容です。
難しい数学の言い方をすると、零元の一意性といいます。
条件を満たすものが一つしか存在しないということを示す良い練習になるかと思います。
線型空間の零元はただ1つ
体 K 上のベクトル空間 V の零元は 0V のみだということを次のようにして証明します。
u ∈ V が、公理⑤の零元の性質を満たしたとします。
そうすると、この u は必ず先ほどから書いている 0V と一致することを示します。
これが示されると、公理⑤を満たす V の元は、必ず 0V であるということになります。
そのため、V の元で公理⑤を満たすものは 0V のみということになります。
では、方針が立ったので、公理⑤を満たす u ∈ V が 0V に一致することを示します。
公理⑤より、u + 0V = 0V
一方、線型空間における加法は、交換可能なので、
0V + u = u + 0V
0V も零元なので、この左辺の値は、u
以上より、u = u + 0V = 0V
これで、公理⑤を満たす u ∈ V は、0V と一致することが証明されました。
体の積と単位元のスカラー倍
1 ∈ K からの作用についての基本的な内容も述べておきます。
公理で、v ∈ V に対して、1v = v でした。
このことを利用すると、次の内容が証明できます。
【命題3】
-1 ∈ K, v ∈ V に対して、
(-1)v = -v
<証明>
1v = v なので、
v + (-1)v = 1v + (-1)v

よって、v + (-1)v = 0V なので、
(-1)v は v の加法についての逆元です。
そのため、
(-1)v = -v【証明完了】
話が飛びますが、ツォルンの補題という記事で無限次元ベクトル空間の基底の存在を示しています。
この記事では、一次独立系の濃度が必ず有限にしかならないベクトル空間についての議論を述べておきます。
補充定理(基底の延長定理)
【補題】
体 K 上の線型空間の基底を、
S = {a1, … , as}, T = {b1, … bt} とする。
このとき、s = t である。
<証明>
T の中には、{a2, … , as} の一次結合で表すことができないベクトルが少なくとも 1 つ存在します。
なぜならば、T のすべてのベクトルが {a2, … , as} の一次結合で表すことができたとすると、矛盾が起きるためです。
T の一次結合で、S のどのベクトルも表せるので、
{a2, … , as} の一次結合で表すことができてしまうことになります。
これは、a1, a2, … , as が一次独立なことに矛盾します。
よって、{a2, … , as} の一次結合で表すことができない T のベクトルを 1 つ取り、それを x1' とおきます。
そうすると、
{x1' , a2, … , as} は一次独立です。
x1' は 基底 {a1, a2, … , as} の一次結合で表せるので、それを次だとします。
x1' = k1a1 + k2a2 + … + ksas
k1 = 0 とすると、x1' が {a2, … , as} の一次結合で表せてしまうことになるので、
k1 ≠ 0 です。
k1 の 体 K における乗法逆元を k1-1 で両辺をスカラー倍させ、移項をすると、
a1 =
k1-1x1+(-k1-1k2)a2+…+(-k1-1ks)as となります。
これは、{a1, a2, … , as} のどのベクトルも、
{x1' , a2, … , as} の一次結合で表せるということを意味します。
そのため、V のどのベクトルも
{x1' , a2, … , as} の一次結合で表せるということになり、
{x1' , a2, … , as} は V の基底となります。
これと同様の操作を
基底 {x1' , a2, … , as} と T について施し、a2 を T のベクトル x2' と取り替えます。
※ x1', a3, … , as の一次結合で表されないから始めて、同様の議論をすることで、a2 を T のベクトル x2' と取り替えることができます。
以下、この操作を繰り返し、
{x1', x2', … , xt', at+1, … , as} という基底を作ります。
この基底には T に含まれているベクトルがすべて含まれているので、
t ≦ s です。
今度は、S を固定して、T のベクトルを S のベクトルへと取り替えます。
同様の議論によって、すべての S のベクトルが置き替えられ T に含まれます。
そのため、s ≦ t となります。
以上より、s = t 【証明完了】
これで、有限次元ベクトル空間の基底を構成するベクトルの個数が一定であることが証明できました。
一定の個数なので、基底を構成するベクトルの個数を有限次元ベクトル空間の次元と定義することができます。
定理の証明
【補充定理】
V を体 K 上の有限次元ベクトル空間とする。
W を V に一致しない部分空間とし、
{w1, … , wm} を W の基底とする。
このとき、いくつかの V の元を W の基底に補充して、V の基底を構成することができる。
<証明>
W が V に一致していないとき、W に含まれていない V の元 v1 が存在します。
この v1 は、w1, … , wm の一次結合で表すことができません。
w1 から wm の一次結合で表される元は、W の元だからです。
v1 は W の元ではないので、そのようなことは起きないということです。
よって、w1, … , wm, v1 は一次独立です。
ここから、再帰性のことを考えます。
{w1, … , wm, v1} で生成される部分空間を W(1) と表すことにします。
W(1) が全体 V と一致していないとき、W(1) に含まれていない V の元 v2 が存在します。
このように、再び始めの設定が繰り返されることになります。
同じ要領で、w1, … , wm, v1, v2 が一次独立ということが証明され、これらで生成される部分空間を W(2) とします。
W(2) が V に一致していなければ、また、W(2) に含まれていない V の元 v3 が存在します。
そして、同様の操作で W(3) という部分空間を作ります。
この操作を繰り返します。
V が有限次元ベクトル空間のときは、基底を構成するベクトルの個数である次元が一定なので、有限回の操作の末に、生成される部分空間が V に一致します。【証明完了】
これで、有限次元ベクトル空間の基底を構成する方法が得られました。
しかし、V が無限次元のときは、際限がなく、今の証明で述べた繰り返し操作は永遠に続いて終わりません。
これについては、基底の濃度という記事で示そうと思います。
【関連記事】
■ 不変部分空間
■ End(V)
読んで頂き、ありがとうございました。
これで、今回の記事を終了します。