ε近傍 | 近傍から集積点、そして閉集合へと理解を広げて【数直線のイメージは大切】
「 ε近傍 」は、ギリシア文字が使われていて、「食わず嫌い」しそうです。
高校や中学で学習した円や球の内部をイメージすると、学習を始めていけるかと思います。
内容が分かるところから始め、そこから大学数学の難しい表現へ徐々に理解を広げていくということが大切になると思います。
学習を進める糸口にまずイプシロン(ε)近傍から。
もし、近傍や集積点の理解が難しいと思われる方がいらっしゃいましたら、具体例を参考にしながら定義の内容と照らし合わせてみると良いかと思います。
このブログでは、実数全体を R と表し、R を n 個で直積をとったものを Rn と表すことにします。
この n 個の直積集合において、距離関数 d をユークリッド距離で定め、n 次元のユークリッド空間として、以下で議論を進めています。
n ≦ 3 のときは、高校数学で学習したピタゴラスの定理を使った二点間距離です。
n 次元だと、成分が n 個出てくるだけと思うと気分が楽になるかと思います。
ε近傍 :定義からスタート
Rn における点 a と、正の実数 ε (> 0) に対して、以下のように 点 a の ε近傍が定義されています。
U(a, ε) = {x∈Rn | d(a, x) < ε}
この点 a を中心とした ε近傍は、点 a との距離が ε 未満となっている Rn の点をすべて集めた集合です。
学習し始めたときに、ε が難しそうに思えるときは、正の実数 t などと思うと気分が晴れます。
n = 2 のときは、点 a を中心とする半径 ε の円の内部に含まれている点をすべて集めたものです。
n が 3 のときは、点 a を中心とする球の内部です。距離 d(a, x) は、二つのベクトルについての二点間距離です。
そのため、それぞれの成分どおしで差をとったものを足し合わせて二乗し、その後で全体にルートをつけた値です。
n = 1 のとき、d(a, x) = |x － a|
このように、n ≦ 3 のときには、高校までの数学で、既に学習しています。
ここからは、大学数学で学習する新しい内容の集積点について説明します。
ε近傍 → 集積点
【集積点の定義】
Rn 内の点 x と集合 A ⊂ Rn について、どんな正の実数 ε に対しても、
A ∩ (U(x, ε) － {x})が空集合ではないとき、点 x を集合 A の集積点という。
この集積点は、定義に差集合と共通部分が使われていることから、嫌がられる定義の一つかと思います。
文章で、この定義を書くと、次のようになります。
どんな正の実数 ε に対しても、「集合 A と、点 x 中心の ε近傍から点 x を除いた集合の共通部分が空集合でない」ときに、点 x が集合 A の集積点。
こういうときこそ、具体的に自分で手ごろな例を通して理解を深めるチャンスです。
ここから具体的に、1 次元のユークリッド空間である直線（数直線）の上で様子を見てみます。
数直線上で見る
集積点の定義の点 x として 7 、集合 A として、{r∈R | 7 ≦ r ≦ 9} を考えることにします。
正の実数 ε (> 0) に対して、点 7 の ε近傍 U(7, ε) は、 {y∈R | |y － 3| < ε}
よって、
U(7, ε) － {7} = {y∈R | |y － 3| < ε} － {7}
※ 1次元より d(7, ε) = |ε － 7|
これで、点 7 中心の ε近傍から 1 点集合 {7} を除外した集合を、ε を使って表すことができました。
「7 － ε より大きく 7 未満である実数」または「7 より大きく 7 + ε 未満である実数」というのが、1 点を除外した集合です。
和集合の形になっています。
どんな正の実数を ε として設定しても、集合 A との共通部分が空集合でなければ、点 7 は集積点ということになります。
{r∈R | 7 ≦ r ≦ 9} が集合 A でしたので、共通部分について確認をしてみます。正の実数は、無限個あるので、場合分けをして確認をします。
ε ≧ 2 または 0 < ε < 2 の二つの場合に分かれます。どんな正の実数 ε に対しても、集合 A との共通部分が空集合でないと、集積点の定義に当てはまりません。
したがって、どちらの場合についても共通部分が空集合ではないことを確認することになります。
【ε ≧ 2 のとき】
7 + ε ≧ 9 なので、集合 A に含まれている 7 より大きくて 9 以下の実数は、すべて U(7, ε) － {7} の中に含まれています。
特に、8∈A であり、
8∈U(7, ε) － {7} なので、共通部分が空集合ではないことが確かめられました。
【0 < ε < 2 のとき】
7 + ε < 9 なので、
U(7, ε) － {7} に含まれている 7 より大きく ε 未満の実数は、A に含まれています。
よって、7 より大きく ε よりも小さい実数 t は、U(7, ε) － {7} と A のどちらにも含まれるということになります。
これで、共通部分が空集合ではないことが確認できました。
※ 2 つの異なる実数 7 と 7 + ε について、この二点の中点を t とすると、より具体性のある証明になります。
以上の場合分けより、点 7 は集合 A の集積点ということが分かりました。
集積点の抽象的な定義は、初めて見ると、よく分からないものかと思います。
しかし、中学一年の数直線で可視化した上で、高校一年生の論理と集合の理解を合わせると、集積点の具体例を得ることができます。
ちなみに、x が、7 より大きくて 9 よりも小さい実数のときも、集合 A の集積点となります。そして、x として 9 も集積点となります。
7 < x < 9 のときは、t < ε を満たす実数 t の範囲と t < 9 を満たす実数 t の範囲の共通部分が、必ず U(x, ε) － {x} の中に含まれるためです。
x = 9 のときも、
9 － ε < t < 9 を満たす実数 t の範囲と、
7 < t < 9 を満たす実数 t の範囲の共通部分が、必ずU(x, ε) － {x} の中に含まれるためです。
集積点ではない点の例
先ほど、A = {r∈R | 7 ≦ r ≦ 9} の集積点の具体例として点 7 などを見つけました。
今度は、集合 A の集積点ではない点を具体的に見てみます。
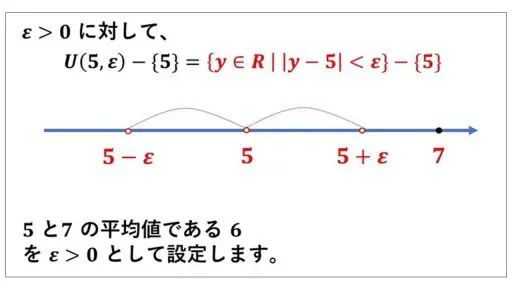
ε = 6 > 0 について、U(6, ε) － {6} と
A = {r∈R | 7 ≦ r ≦ 9} の共通部分は空集合になっています。
したがって、どんな正の実数 ε に対しても、共通部分が空集合ではないという条件に当てはまりませんでした。
このため、点 6 は集合 A の集積点ではないということが分かります。
実は、A の外部の点 p について、p < 7 のときは、p と 7 の平均値を ε と設定すると、
U(p, ε) － {p} と A の共通部分が空集合になってしまします。
つまり、U(p, ε) － {p} ∩ A = Φ
p > 9 のときには、
p と 9 の平均値を ε とすると、共通部分が空集合になってしまいます。
そのため、閉区間 A の外部の点は、集積点ではないということになります。
ここまでの具体的な理解ができると、閉集合の定義にチャレンジできます。
ε近傍 :そして閉集合へ
【閉集合の定義】
A ⊂ Rn について、A の集積点全体を C(A) と表すことにする。
C(A) ⊂ A となっているときに、A を閉集合 (closed set) という。
C(A) という記号を導入しました。
要するに集合 A について、「集合 A の集積点が、必ず集合 A に含まれているということが成立しているとき」に、A を閉集合といいます。
【閉集合の具体例】
A = {r∈R | 7 ≦ r ≦ 9} という閉区間は、閉集合になっています。
先ほどの考察で、7 以上 9 以下の実数は、どれも A の集積点でした。そして、外部の点は、どの点も集積点ではありませんでした。
このことから、A の集積点は、すべて A の中に含まれているため、A は閉集合です。
【閉集合ではない例】
B = {r∈R | 7 < r ≦ 9} は、閉集合ではありません。
理由は、上で具体的に考察した結果から、点 7 は B の集積点です。
しかし、点 7 は B に含まれていません。そのため、C(B) が B の部分集合にならないため、閉集合ではありません。
練習に、ちょっとした命題を証明するのも良いかと思います。
閉集合に関連する命題
Rn の部分集合 A が閉集合とする。
S を A の部分集合とし、s∈Rn を S の集積点とする。
このとき、s∈A となる。
【証明】
s∈Rn が S の集積点より、任意の正の実数 ε に対し、
S∩(N(s, ε) － {s}) は空集合ではありません。
S∩(N(s, ε) － {s}) は、
A∩(N(s, ε) － {s}) の部分集合であるので、
A∩(N(s, ε) － {s}) も空集合でないということになります。
ε は任意の正の実数なので、どんな正の実数 ε についても、1点を除いた集合との共通部分が空集合ではないことが確認できたので、s は A の集積点です。
したがって、A は閉集合なので、閉集合の定義から、A の集積点は必ずその中に含まれるので、s∈A と結論づけられます。【証明終了】
＜証明の補足説明＞
x∈S∩(N(s, ε) － {s}) とすると、
x∈S かつ x∈N(s, ε) － {s} となります。
S⊂A なので、x∈A に注意すると、
x∈A かつ x∈N(s, ε) － {s} が成立しています。
このようなところで、集合と論理についての考察が役に立ちます。
そのため、高校のときから論理と集合を意識しておくと、大学数学が理解しやすいかと思う次第です。
ここからは、部分列や点列を解説をしています。微分積分を学習するときに、基礎となる内容になります。
以下の内容で使う記号です。自然数全体を N とし、実数全体を R と表しています。
また、自然数 n について、Rn を n 次元ユークリッド空間とし、二点間の距離を d (a, b) というように表しています。
ε近傍 :点列と部分列へ
数列 a : N → R と、N から N への単調増加関数 φ について、合成関数 a・φ を数列 a の部分列といいます。
連続関数の最大・最小値の存在を示す定理より
※単調増加関数とは、k < l ならば、φ(k) < φ(l)となる関数です。
数列 {an} の部分列の定義が、抽象的で、はじめて見ると理解しにくいものかと思います。
部分列を理解するには、例を通じて考えると良いかと思います。
一つ一つの内容は、高校数学で学習している内容で、それらが組み合わさって部分列が構成されています。
この内部構造を、焦らずに正確に確認すると、意外と親近感のある定義です。
ゆっくりと知っている例から
まず実数列は、自然数全体 N の各要素に対して、実数を対応させる関数です。
この内容は、数学3の参考書などを読むと、地味ですが言及されているかと思います。そして、部分列に関わってくるのが合成関数です。
ですので、単調増加関数と数列の合成関数が、その数列の部分列ということになります。
文章で書くと、このように長く難しそうになってしまいますが、論より証拠で、例を見てみます。
数列{an} による対応を、n∈N についての対応を an = a(n) と表すことにします。
【例】an = 5n (n∈N)
第 1 項の値が、a(1) = a1 = 5 × 1 です。一般に、自然数 k を n に代入すると、第 k 項の値 ak が 5k となっています。
N から N への単調増加関数 φ として、次の具体例を考えます。
【例】φ(m) = 3m (m∈N)
合成関数 a・φ が、部分列です。部分列が、どのような対応になっているのかを洞察してみます。落ち着いて、ゆっくりと対応を合成関数の定義に基づいて確認します。
1 という自然数に対して、部分列は、次の流れで対応させる実数を決定します。
- 1 に対して φ(1) = 3 × 1 = 3 という値を認識
- φ(1) という自然数に対して、数列（関数）a で対応する値を求める
→ a(φ(1)) = a(3) = a3
= 5 × 3 = 15 - a・φ(1) = 15 と部分列によって、1 に対応する値が決定
この部分列という関数 a・φ が、どのようなプロセスで 1 という定義域に含まれている要素に実数を対応させているかを洞察しました。
このインサイト、文字を使って一般化します。
m∈N に対して、
a・φ(m) = a(3m) = a3m
= 5 × (3m) = 15m
これで、どんな自然数 m についても、部分列という関数が対応させる実数が何であるかを確定できました。
例えば、自然数 7 に対応させる値は、
15 × 7 を計算して 105 と分かります。
このように、具体的なアルゴリズムを見切ることができると、数学が分かってくるかと思います。
これで、部分列について理解してきたら、抽象的な理論の証明で部分列を見てみると、理解が広がります。
ε近傍 :見切った内容から
Rn 内の点 x と集合 A ⊂ Rn について、どんな正の実数 ε に対しても、
A ∩ (U(ε, x) － {x}) が空集合でないとき、点 x を集合 A の集積点という。
U(ε, x) は、点 x との距離が ε 未満である Rn の点をすべて集めた集合で、ε近傍といいます。
ここから、一点集合 {x} との差集合と A との共通部分が空集合でないのかどうかが議論されます。
また、数列の一般化で点列という関数があります。
k 次元ユークリッド空間についての点列は、自然数 n に対して、Rk 内の点を対応させる関数です。an の値が、k 個の成分からなる座標になったというものです。
部分点列の定義は、先ほどの部分列と同様です。N から N への単調増加関数 φ との合成関数となります。
では、ここから、抽象的な理論の証明です。
点列を使った書き換え
【定理】
m を自然数とする。
A ⊂ Rm について、x∈Rm が集合 A の集積点であることの必要十分条件は、x に収束する点列 {an} で、各自然数 n について、an∈A かつ an ≠ x を満たすものが存在することである。
＜証明＞
まず、点 x が集合 A の集積点だとすると、このような点列が存在することを証明します。
点 x∈Rm を集合 A の集積点とすると、次のようにして、N から Rm への点列（関数）が定義できます。
任意の自然数 n に対して、その逆数 1/n も正の実数なので、点 x が集積点であることから、
A ∩ (U(1/n, x) – {x}) ≠ Φ より、
A ∩ (U(1/n, x) – {x}) に含まれる点 b(n) が存在します。
※ 2 つ以上の点が存在するとき、どれでも良いので 1 つ取り b(n) とします。
この b(n) を 自然数 n に対応させる Rm 内の点として、a(n) = an = b(n) と表すことにします。
※ これで点列が定義できました。
さらに、それぞれの定義と照らし合わせて、細かく見てみます。
点列の定め方より、任意の自然数 n に対して、
an = a(n)
∈ A ∩ (U(1/n, x) – {x}) ⊂ A
また、a(n) ∈ U(1/n, x) なので、近傍の定義から、d(a(n), x) < 1/n
n を十分大きくすると、1/n は 0 に限りなく近づくので、a(n) は 点 x に収束します。
さらに、a(n) A ∩ (U(1/n, x) – {x}) ということから、a(n) ≠ x です。
これで、点列 {an} は、点 x に収束することが示せました。
この内容をイプシロンエヌ法の定義で表しておきます。
任意の正の実数 ε に対して、ある自然数 k が存在して、「 n ≧ k ならば、1/n < r 」となることから、n ≧ k ならば、d(a(n), x) < 1/n < r となるため、点列 {a(n)} が点 x に収束する。
次に、点 x に収束する点列 {an} で、各自然数 n について、an∈A かつ an ≠ x を満たすものが存在すれば、点 x が集合 A の集積点であることを証明します（今度は逆向きの証明です）。
仮定より、点列{an} が点 x に収束します。そのため、「任意の正の実数 ε に対して、ある実数 k が存在して、n ≧ k ならば、d(an, x) < ε 」となります。
以下、任意の正の実数 ε に対して議論をします。
d(ak, x) < ε なので、ak∈U(ε, x) となっています。そして、仮定より ak∈A です。
よって、ak∈A ∩ U(ε, x)
仮定より、ak ≠ x なので、
ak∈A ∩ (U(ε, x) － {x})
ak が含まれているので、この共通部分は、空集合ではありません。
以上より、任意に与えられた正の実数 ε に対して、A ∩ (U(ε, x) － {x}) が空集合でないことが示せました。
これは、集積点の定義を満たしたということです。
すなわち、点 x が集合 A の集積点ということが示せました。【証明終了】
定義に照らし合わせながら、近傍や集積点が証明の中でどのように使われているのかを考えると、段々と理解が深まるかと思います。
関連する記事として、イプシロンデルタ論法という記事を投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。