関数の和 | 微分可能な関数の和の導関数を定義に基づいて求める【関数のスカラー倍についても】

微分可能な実数値関数 f(x) と g(x) について、" 関数の和 “である f(x)+g(x) の導関数を求めます。
また、実数 r を用いて、関数のスカラー倍 rf(x) の導関数も同じ要領で求めることができます。
そうすると、自動的に rf(x)+kg(x) の導関数を求める方法を証明したことになります。
まずは、関数の和の定義と、関数をスカラー倍することの定義を確実に押さえるところから、数3の導関数の学習を始めることが大切になります。
微分可能ということの定義から、それぞれの導関数を導きます。
関数の和 :和の定義から
実数全体を定義域とし、各実数に対して実数を対応させる関数を f と g とします。
このとき、f+g という関数の和を次のように定義します。
各実数 x に対して、f(x) と g(x) という二つの実数の和を対応させる関数を f と g の和といいます。
関数の和を表す記号が、f+g です。
x に対応させる実数を (f+g)(x) = f(x)+g(x) と表します。
これで、二つの実数値関数の和を定義することができました。
さらに、f と g が微分可能な関数のときに、関数の和も微分可能で、f の導関数と g の導関数を使って、f+g の導関数を表すことができます。
ちなみに、関数 f が微分可能であるとは、
Δx → 0 としたときに、
{f(x+Δx)-f(x)}/Δx が収束することです。
より詳しくは、右極限と左極限が同じ値に収束するということです。
この微分可能ということの定義に基づいて、関数の和の導関数を求めます。
f+gの導関数
【命題1】
実数全体を定義域とする実数値関数 f と g が微分可能であるとする。
このとき、
{f(x)+g(x)}’ = f'(x)+g'(x) である。
<証明>
y = (f+g)(x) と置くことにします。
関数の和の定義から、x の増分 Δx に対して、
(f+g)(x+Δx) = f(x+Δx)+g(x+Δx)
また、(f+g)(x) = f(x)+g(x) です。
そのため、y の増分 Δy は、
Δy = (f+g)(x+Δ)-(f+g)(x)
= f(x+Δx)+g(x+Δx)-f(x)-g(x)
= f(x+Δx)-f(x)+g(x+Δx)-g(x)
両辺に 1/Δx を掛けると、
Δy/Δx =
{f(x+Δx)-f(x)}/Δx+{g(x+Δx)-g(x)}/Δx
ここで、f と g が微分可能であるから、
Δx → 0 のとき、
{f(x+Δx)-f(x)}/Δx → f'(x),
{g(x+Δx)-g(x)}/Δx → g'(x) となります。
よって、Δx → 0 のとき、
Δy/Δx → f'(x)+g'(x) です。
よって、関数 y = f(x)+g(x) の導関数が、
f'(x)+g'(x) と分かりました。【証明完了】
今度は、関数のスカラー倍と、スカラー倍された関数の導関数を求めます。
関数の和 :関数のスカラー倍も考える
f を定義域を実数全体とする実数値関数とします。
このとき、実数 r による f のスカラー倍 rf を次のように定義します。
実数 x に対して、
rf(x) = r × f(x) を対応させるのが、rf というスカラー倍された関数です。
rf は、実数 x に対して、f(x) という実数と r の積を対応させています。
f が微分可能であるときに、rf も微分可能であることを、関数の和のときと同じような要領で証明します。
スカラー倍された関数の導関数
【命題2】
定義域を実数全体とする実数値関数 f が微分可能であるとする。また、r を実数とする。
このとき、rf は微分可能であり、
{rf(x)}’ = r × f'(x) となる。
<証明>
y = rf(x) と置きます。
Δy = (rf)(x+Δx)-(rf)(x)
= rf(x+Δx)-rf(x)
= r{f(x+Δx)-f(x)}
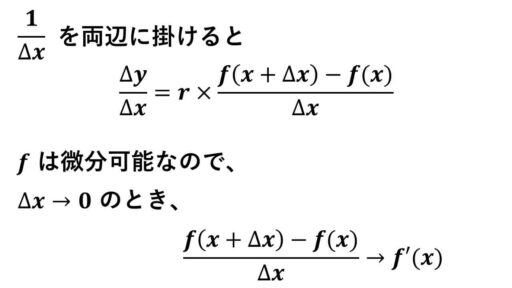
よって、Δx → 0 のとき、
Δy/Δx → r × f'(x)【証明完了】
これで、スカラー倍された関数の導関数も求まりました。
【命題1】と【命題2】の内容を合わせると、次の【命題3】が得られます。
関数の和 :rf(x)+kg(x)の導関数
【命題3】
r と k を実数とし、f と g を定義域が実数全体である微分可能な実数値関数とする。
このとき、
{rf(x)+kg(x)}’ = rf'(x)+kg'(x) である。
<証明>
【命題2】より、
{rf(x)}’ = rf(x),
{kg(x)}’ = kg(x) です。
関数 rf と kg の和についての導関数が、【命題1】から得られます。
よって、
{rf(x)+kg(x)}’
= {rf(x)}’+{kg(x)}’
= rf'(x)+kg'(x)【証明完了】
この【命題3】を具体例を通じて使う練習をしてみます。
具体例で練習
【例】
関数 f は、実数 x に対して f(x) = x2 を対応させているとします。
また、g は x に対して g(x) = 3x+1 を対応させているとします。
このとき、
y = (2f+3g)(x) = 2x2+9x+3 の導関数を求めてください。
f も g も微分可能な関数なので、【命題3】を使います。
y = 2x2+9x+3
= {2f(x)}+{3g(x)} だから、
y’ = 2f'(x)+3g'(x)
ここで、f'(x) = 2x, g'(x) = 3 より、
y’ = 4x+9 です。
【命題1】と【命題2】を使って、微分と積分の関係で基本となる内容を証明しておきます。【命題3】の不定積分版になります。
積分してから微分する
f(x) と g(x) の原始関数の一つをそれぞれ F(x) と G(x) とします。そして、F(x) と G(x) が x で微分可能だとします。
原始関数は、微分すると元の関数に戻ります。
∫ f(x) dx = F(x)+C1,
∫ g(x) dx = G(x)+C2 となっています。
ここで、C1 と C2 は積分定数です。
実数 r と k を定数とすると、
rF(x) と kG(x) は関数なので、和を考えることができます。
そこで、【命題1】を使います。
{rF(x)+kG(x)}’ = {rF(x)}’+{kG(x)}’ です。
さらに、【命題2】を使うと、
{rF(x)}’ = r{F(x)}’ = rf(x),
{kG(x)}’ = k{G(x)}’ = kg(x) となります。
これらは、rf(x) の原始関数の一つが rF(x) で、kg(x) の原始関数の一つが kG(x) ということを意味しています。
そして、
{rF(x)+kG(x)}’ = rf(x)+kg(x) です。
これは、rf(x)+kg(k) という関数の原始関数の一つが、
rF(x)+kG(x) ということを意味しています。
よって、
∫ {rf(x)+kg(x)} dx = rF(x)+kG(x)+C(C は積分定数)となります。
rf(x), kg(x) の原始関数の一つが、それぞれ rF(x), kG(x) だったので、
rF(x)+kG(x)+C = ∫ rf(x) dx+∫ kg(x) dx ということになります。
これらを合わせると、
∫ {rf(x)+kg(x)} dx = ∫ rf(x) dx+∫ kg(x) dx となります。
また、【命題2】から、
{rF(x)}’ = r{F(x)}’ = rf(x) なので、
rf(x) の原始関数の一つが rF(x) です。
rF(x) は f(x) の原始関数の一つに r を乗じたものなので、
∫ rf(x) dx = rF(x)+C3 = r∫ f(x) dx となります。
(C3 は積分定数です。)
同様に、
∫ rg(x) dx = rG(x)+C4 = r∫ g(x) dx となります。
(C4 は積分定数です。)
よって、
∫ {rf(x)+kg(x)} dx = ∫ rf(x) dx+∫ kg(x) dx
= r∫ f(x) dx+r∫ g(x) dx
【命題1】と【命題2】(もしくは【命題3】)は、微分の計算をするときに、導関数の性質として基本的となります。
関数の和について述べてきましたが、数IIIの定義に基づいた証明になれるために、基礎となる内容を導いておきます。
n乗の微分と導関数について
y = f(x) = xn(n は自然数)について、導関数を求めます。
h > 0 として、x が x から x+h まで変化するときの平均変化率を考えます。
f(x+h) = (x+h)n なので、二項展開の公式を使うチャンスです。
f(x+h) = ΣrnCrxn-rhr となります。
r が 0 以上 n 以下の非負整数を動きます。
Δy = f(x+h)-f(x) を考えたときに、各 r について、それぞれの項を見てみます。
【r = 0 の項】
nC0xn-0h0-xn = xn-xn = 0
【r ≧ 1 の項】
nCrxn-rhr と h が残っています。
よって、Δx = (x+h)-x = h についての平均変化率を計算したとき、Δy/Δx の各項は、次のようになっています。
【r = 0 の項】
0 ÷ h = 0 と消えています。
【r ≧ 1 の項】
nCrxn-rhr ÷ h = nCrxn-rhr-1
よって、
Δy/Δx = ΣrnCrxn-rhr-1 (ただし、r は 1 以上 n 以下の自然数を動きます。)
Δx → 0 のとき、h → 0 なので、
Δy/Δx の項について、r ≧ 2 の項は h の指数が 1 以上なので、0 へ近づきます。
そのため、h → 0 のときに、残るのは r = 1 の項のみです。
Δy/Δx の r = 1 の項は、
nC1xn-1h1-1 = nxn-1 です。
よって、h → 0 のとき、
Δy/Δx → nxn-1 となります。
これで、y = f(x) = xn について、
f'(x) = nxn-1 という公式が導けました。
二項展開の公式を使うときに、r = 0, 一般項、r = n の三つについて考察をすることが多いです。
見た目が複雑な二項展開の式ですが、r = 0 や r = n といった具体的な項から一般項まで冷静に値を確認することで、証明の完成が見えてくるときがあります。
xn の微分の公式を導関数の定義に基づいて求めるときに、Δy について、r = 0 の項が消えるということを足掛かりにして議論を進めました。
※ 微分係数の定義に基づいた数3の証明として、ロルの定理という記事を投稿しています。
基礎をしっかりと押さえておくと、大学の数学へも理解が広がります。
関数の和 :抽象的なベクトル
高校数学のCで学習するベクトルは、大きさをもった有向線分です。矢印とは関係のないものも、大学の数学ではベクトルという線形代数の元(要素)として考えます。
その具体例と一つが、先ほど証明した実数全体を定義域とする微分可能な実数値関数です。
R を実数全体とし、
V を実数全体を定義域とする微分可能な実数値関数をすべて集めた集合とします。
すると、【命題1】から、
f, g∈V に対して f+g∈V ということになります。
微分可能な関数の和も微分可能な関数ということです。
また、r∈R, f∈V とすると、
【命題2】より、rf∈V となります。
微分可能な関数を実数でスカラー倍しても微分可能な関数です。
この V における関数の和と関数のスカラー倍について、ベクトル空間の公理を満たすことが分かります。
どの実数 x に対しても 0 を対応させるという定数関数が V の零元となります。
ベクトル空間の公理の条件をすべて確かめると長くなりますが、一つ一つは、この記事で述べた関数の和の定義とスカラー倍の定義から容易に確認することができます。
よって、V は R 上のベクトル空間(線形代数)となっています。
※ 大学の内容について、無限次元ベクトル空間という記事を投稿しています。
結合法則(結合律)については、高校の数学で、あまり馴染みがないかと思いますので、関数の和についての結合法則だけ、確かめておきます。
関数の加法の結合法則
f, g, h∈V とし、x を実数とします。
(f+g)+h = f+(g+h) となることの証明は、定義域である実数全体 R のどの元 x についても、左辺による対応と、右辺による対応が同じになっていることを示すことになります。
{(f+g)+h}(x) = (f+g)(x)+h(x) です。
これは、f+g と h の関数の和の定義です。
さらに、f と g の関数の和の定義から、
(f+g)(x) = f(x)+g(x) です。
まとめると、
{(f+g)+h}(x) = {f(x)+g(x)}+h(x) です。
f(x), g(x), h(x) は、実数なので、実数についての加法の結合法則から、次を得ます。
{f(x)+g(x)}+h(x) = f(x)+{g(x)+h(x)} です。
そのため、
{(f+g)+h}(x) = f(x)+{g(x)+h(x)} です。
この右辺は、
f(x)+{g(x)+h(x)} = {f+(g+h)}(x) です。
よって、
{(f+g)+h}(x) = {f+(g+h)}(x)
定義域のどの元 x についても、x に対応させる実数が等しいということが分かりました。
二つの関数が等しいことの定義より、
{(f+g)+h} = {f+(g+h)} です。
これで、関数どおしの加法について、結合法則が成立することが確認できました。
実は、結合法則が成立すると、一般個数の元について、括弧のつけ方に依らずに二項演算の値が確定するという一般の結合律が成立します。
※ 結合律というブログ記事で、一般の結合律を帰納法を用いて証明しています。
4 個以上についての結合法則は、一般の結合律の証明を理解しなくても、高校の数学では自由に使って大丈夫です。
4個の関数の導関数
実数 x に対して、それぞれ x4, 2x3, 3x2, 4x4 を対応させる関数たちの和の導関数を求めてみます。
y = x4+2x3+3x2+4x の導関数を求めます。
括弧のつけ方に依らないということから、
y = (x4+2x3)+(3x2+4x) と考えることができます。
よって、関数の和の微分より、
y’ = (x4+2x3)’+(3x2+4x)’
= (x4)’+(2x3)’+(3x2)’+(4x)’
= 4x3+6x2+6x+4
4個以上の和について、括弧のつけ方に依らずに計算できるということを意識して、計算しやすい形で導関数を計算できます。
ちなみに、
y = x4+{2x3+(3x2+4x)} として導関数を計算しても、同じ導関数になっています。
y’ = (x4)’+{2x3+(3x2+4x)}’
= 4x3+(2x3)’+(3x2+4x)’
= 4x3+6x2+(3x2)’+(4x)’
= 4x3+6x2+6x+4
y’ は、同じ導関数となっています。これが、括弧のつけ方に依らないということです。大学の数学を学習するときは、このような括弧のつけ方を意識するときもあるので、取り挙げました。
途中で不定積分についても述べましたが、置換積分についての記事も関連内容として投稿しています。
それでは、今回の記事を終了します。
読んで頂き、ありがとうございました。