放物線の軸 M(a) という関数 | 場合分けで端が動く最大値問題を解く練習

" 放物線の軸 “と M(a) という関数の最大値問題について、場合分けをする問題が出題されることがあります。
起こり得る可能性を論理的に場合分けて、すべての場合について結論を求めることが大切になります。
また、背後にある関数の対応についての考察は、数学2や数3へとつながるので、高校一年の段階から、考える練習をしておくと良いと思われます。
まさに、高校の数学らしい関数の対応を、論理で考える問題になります。
関数の対応ということを意識し、何に対して、何を対応させるのかということを捉えることが決め手になります。
はじめに、問題の背景となる関数の対応について説明をします。
その後で、典型的な二次関数のグラフである放物線の最大値についての具体的な問題を解説します。
放物線の軸 : M(a) は何と何が対応する関数なのか
【問題】
a を正の実数とし、0 ≦ x ≦ a における関数
f(x) = x2 -4x + 2 の最大値を M(a) とします。
このとき、M(a) という a に応じて定まる関数を a の式で表してください。
高校一年の数学1で出てきそうな問題です。
この問題で、y = f(x) と二次関数は、具体的に係数が設定されてあるので、計算をすると軸の方程式や、頂点の座標を求めることができます。
ただ、中学の数学のときには、意識しないような関数の対応が背後にあります。
正の実数 a に応じて、M(a) という実数を対応させる関数について問われています。
関数を a の式で表すということですが、学習し始めた頃には、イマイチ分かりにくい内容かと思います。
この関数を定める式というものについて、理解を深めてから、問題に臨みます。
y = f(x) という関数だと、各実数 x に対して、f(x) という値を対応させています。
f(x) の値は、x2 -4x + 2 の x に具体的な実数を代入することで定まります。
一方、関数 M(a) だと、
正の実数 a に対して、
「0 ≦ x ≦ a における関数 f(x) = x2 -4x + 2 の最大値」を対応させると問題文に書いてあります。
この内容を理解することができると、関数 M(a) を定めている式が見えてきます。
M(a) という関数
今回の問題では、正の実数 a の値に応じて、
0 ≦ x ≦ a の右端の値が変化します。
そのため、f(x) = x2 -4x + 2 の最大値が、a の変化に連動して変化します。
ここで、「a の値に応じて 0 ≦ x ≦ a における f(x) の最大値を対応させる」という関数 M(a) の定義が効いてきます。
f(x) = (x - 2)2 - 2 なので、x = 2 が軸を表す方程式で、(2, -2) が頂点の座標です。
二次関数のグラフである放物線は、軸に対して線対称な図形です。
そのことから、図形的に、どこで二次関数が最大値をとるのかということを場合分けて考えます。
そうすることで、a に応じて変化する二次関数の最大値というものが分かってくるかと思います。
ここからは、図を使って、二次関数の最大値が、どんな x に対してとるのか。
そして、最大値と a の関係が、どうなっているのかを解説します。
放物線の軸 :グラフで図形的に考察
【練習問題】
a を正の実数とし、0 ≦ x ≦ a における関数
f(x) = x2 -4x + 2 の最大値を M(a) とします。
このとき、M(a) という a に応じて定まる関数を a の式で表してください。
a の値によって、二次関数の定義域が変化し、そのために f(x) の最大値をとる場所が変わるということを図から考察します。
f(x) = (x - 2)2 - 2 (0 ≦ x ≦ a) の軸は、
x = 2 です。
f(x) の定義域 0 ≦ x ≦ a の中央の値 a/2 が
[1] 2 より小さいとき、
[2] 2 に等しいとき、
[3] 2 より大きいとき
と場合分けをして考えます。
a/2 という正の実数の値は、[1]、[2]、[3] のうちのどれかに必ずなるということが論理的に分かります。
そこで、図を用いて、f(x) の定義域の中央の値 x = a/2 より左側での y 座標の増減と、右側での y 座標の増減を見比べます。
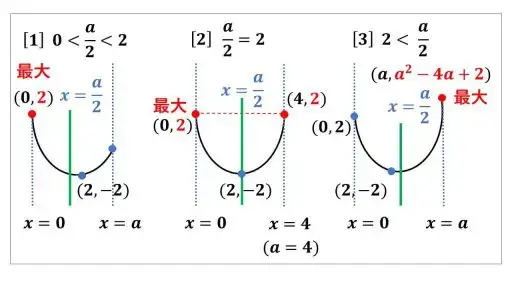
[1] の場合、定義域の中央の値 a/2 と a の間に軸の x 座標 2 があります。
a/2 から a までの変化は、a/2 から 2 までの y 座標の値が減少した後で、上昇します。
一方、0 から a/2 までの y 座標の変化は、ずっと y 座標の値が減少しています。
よって、[1] のとき関数 f(x) の値域は -2 ≦ f(x) ≦ 2 となり、最大値は 2 です。
[2] の場合は、a = 4 ということで、左右対称です。
-2 ≦ f(x) ≦ 2 が値域になり、最大値は 2 です。
[3] の場合は、-2 ≦ f(x) ≦ a2 -4a + 2 が値域になります。この中で、x = a で最大となるのは、やはり放物線のグラフの対称性からです。
[1] のときとは、軸の左右で起きていることが反対になっている感じです。
x = 2 から x = 4 まで、
(a/2 - 2) + a/2 の幅で、放物線上の y 座標が増加し続け、x = 2 から x = 0 までの y 座標の増加よりも大きくなっています。
そのため、x = a で最大値 a2 - 4a + 2 をとります。
図が微妙なときは、論理的に放物線が左右対称であることから、y 座標の値の大小を判断することが大切になります。
※ テストのときに、自分で図をフリーハンドで描くと、微妙なときが出てきます。
その際に、論理的に考察を進められるかがポイントになる単元です。
では、正の実数 a に応じて対応させる f(x) の最大値 M(a) のことをまとめます。
場合分けのまとめ
【まとめ】
[1] 0 < a/2 < 2 または [2] a/2 = 2 の場合
つまり、0 < a < 4 または a = 4 の場合
→ M(a) = 2
[3] 2 < a/2 の場合
つまり、4 < a の場合
→ M(a) = a2 - 4a + 2
0 < a ≦ 4 のときは、
M(a) = 2 という定数関数です。
4 < a のときは、
M(a) = a2 - 4a + 2 と二次関数になっています。
このように、f(x) の軸と定義域の関係から、M(a) の関数の対応を与える式が変化することがあります。
この問題は、関数 M(a) の式を a を用いて表すことだったので、
M(a) = 2 (0 < a ≦ 4 のとき),
M(a) = a2 - 4a + 2 (4 < a のとき)
が、答えとなります。
正の実数 a に対して、
関数 f(x) = x2 -4x + 2 が 0 ≦ x ≦ a においてとる最大値 を対応させる関数が M(a) でした。
関数の対応では、何に対して、何を対応させるのかということを把握することが大切になります。
【関連する記事】
■ 要素(元)
■ 平方完成
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。