イプシロンデルタ論法 (ε-δ論法) の答案の書き方で意識すると良いこと
イプシロンデルタ論法 について、「書き方で意識すること」を解説しています。
ε-δ 論法の解説と合わせて、記事の後半でイプシロンエヌ法の書き換えについても説明しています。
関数が連続であることを証明するときに使うのが、ε-δ 論法 です。
論法といっても、関数が連続であることの定義を確認して、「確かに連続です」という答案を書くのだと思っておくと気持ちが楽かと思います。
イプシロンデルタ論法 :関数の連続性の定義
【関数が連続であることの定義】
関数 y = f(x) のグラフが、
xy 座標平面上の点 (p, f(p)) において連続であるとは、次を満たすことである。
任意の正の実数 ε に対して、正の実数 δ が存在して、
「 |x-p| < δ ならば |f(x)-f(p)| < ε 」を満たす。
数学では、一つひとつの記号をどのように使うかは、明確に定まっていません。
ですので、記号を使うときには、この記号は何かということを明確に定めておかなければなりません。
「 |x-p| < δ ならば |f(x)-f(p)| < ε 」の部分の不等式を証明することをしっかりと書くのも大切ですが、与えられた ε に対して、正の実数 δ をどのように設定したのかも明確に記述しなければなりません。
プログラミングで、定義を記述していないものをいきなり使うとエラー表示になるのと同じように、数学でも明確に δ をどう設定したのかを書いておかなければなりません。
それでは、イプシロンデルタ論法で答案を記述するときの留意点は何かということを書いておきます。
イプシロンデルタ論法の留意点
① 与えられた正の実数 ε に対して、正の実数 δ をどのように設定したかを記述する。
② 設定した δ を使って、連続の定義である 「 |x-p| < δ ならば、 |f(x)-f(p)| < ε 」 という内容が満足されていることを示す。
この①と②の両方を答案に記述すると、関数の連続性の定義を示せたということになり、レポートが受理されるかと思います。
②の部分は、たいてい不等式の変形が大変です。
そのため、不等式にだけ目を向けていると、①が疎かになりがちになります。
答案を提出する前に、①の部分を適切に記述できているかも確認です。
では、シンプルな練習問題を使って、イプシロンデルタ論法を使った答案を作成してみます。
イプシロンデルタ論法 :練習問題
【練習問題】
f(x) = 0.1x という関数(定義域は実数全体)が、点 (p, f(p) ) において、連続であることを示してください。
この f(x) は、中学一年の数学で学習する正比例の関数です。
知識として、連続関数であることを高校数学までの段階で知っていますが、シンプルな例で連続性を確認してみます。
では、先ほどの留意点を押さえた上で、答案を作成してみます。
適宜、注釈を書いていますが、あくまで太字の部分が答案と思ってご覧頂ければと思います。
<答案>
実数 ε > 0 が与えられたとする。
このとき、δ = 10ε と定めると、実数 δ > 0 である。
※ 確かに、ε に応じて δ という正の実数を設定しました。①の部分は完了したので、②の部分を確かめます。
ここで、xの値が|x-p|<δと仮定する。
今、|x-p|<δ = 10ε、
すなわち、|x-p|<10ε … (1)
f(x) = 0.1x, f(p) = 0.1p より、
|f(x)-f(p)| = |0.1x-0.1p|
= |0.1|×|x-p|
つまり、
|f(x)-f(p)| = 0.1 × |x-p| … (2)
よって、(2) に (1) を代入すると、
|f(x) - f(p)| < 0.1 × 10ε
ゆえに、|f(x) - f(p)| < ε
したがって、関数 f(x) は、点 (p, f(p)) において連続である。【証明完了】
連続であることの定義を満たすことが示されたということです。
このように、まず①「ε に応じて δ をどう設定するか」を記述します。
その上で、② 「 |x-p| < δ ならば |f(x)-f(p)| < ε 」 という内容が満足されていることを示すという流れになります。
ちなみに、今回の証明で、どのようにして、δ として設定した値を決めたかということを書いておきます。
最終の到達したい結論が|f(x)-f(p)|<εなので、結論から逆算したというわけです。
f(x) の定義から、|0.1x-0.1p| < ε となれば良いので、0.1 × |x-p|<ε
この不等式の両辺を10倍すると、
|x-p| < 10ε となります。
このように逆算をして、10ε を δと定めたわけです。
複雑な不等式になるときは、逆算しようにも、うまく見つからないときもあるかと思います。
とりあえず、難しい不等式とは分離し、イプシロンデルタ論法の留意点を押さえ、型をつくるという内容に重きを置いて、今回のブログを書きました。
※ ちなみに、有界閉区間において定義された連続関数は、その値域において最大値と最小値をもつという定理があります。
ここから、大学の微分積分の学習で基礎となる、連続関数についての命題を証明します。
連続関数のスカラー倍も連続関数
【命題】
実数全体を定義域とする実数値連続関数 f が連続関数だとします。
このとき、実数 r によってスカラー倍された rf も連続関数です。
特に、x = p (p は実数) において連続です。
ここで、スカラー倍された関数がどのような対応をするのかを押さえておきます。
定義域に含まれている実数 x に対して、関数 f は f(x) という実数を対応させています。
このことを利用して rf の対応が決められています。
(rf)(x) = r × f(x) が、スカラー倍された関数 rf による対応です。
実数 x に対して、実数 r × f(x) を対応させています。つまり、f(x) を r 倍した実数を対応させる関数というわけです。
では、命題をイプシロンデルタ論法で証明します。任意に取った実数 p について、x = p において連続であることを示します。
<証明>
任意に正の実数 ε が与えられたとします。
r = 0 のときは、関数 rf は、常に 0 を対応させるという定数関数なので、δ = 1 などと、適当な正の実数を δ として当てはめると、ε で次のように押さえこめます。
|x - p| < δ とすると、
|(rf)(x) - (rf)(x)|
= |0 - 0| < ε
ε は正の実数なので、0 よりも大きいので、押さえ込むことができました。
このときは、自明だったので、r ≠ 0 のときを以下で扱います。
r ≠ 0 のとき、分母に r をもってくることができるので、ε / |r| > 0 という正の実数 ε / |r| を定めることができます。
仮定より、関数 f は連続なので、この正の実数 ε / |r| に対して、正の実数 δ が存在して、
|x - p| < δ ならば、
|f(x) - f(p)| < ε / |r| … ★

これで、関数 rf は、x = p において連続であることの定義を満たしたので、結論を示せました。【証明完了】
任意に与えられた正の実数 ε に対し、
正の実数 δ が存在して、
「|x - p| < δ ならば、|(rf)(x) - (rf)(p) < ε」ということを示せました。
実数 x が実数 p に十分近い値のときに、実数(rf)(x) の値は実数 (rf)(x) の値に十分近いという極限概念の内容です。
この証明と同じような要領で、連続関数どおしの和も連続関数ということが示せます。
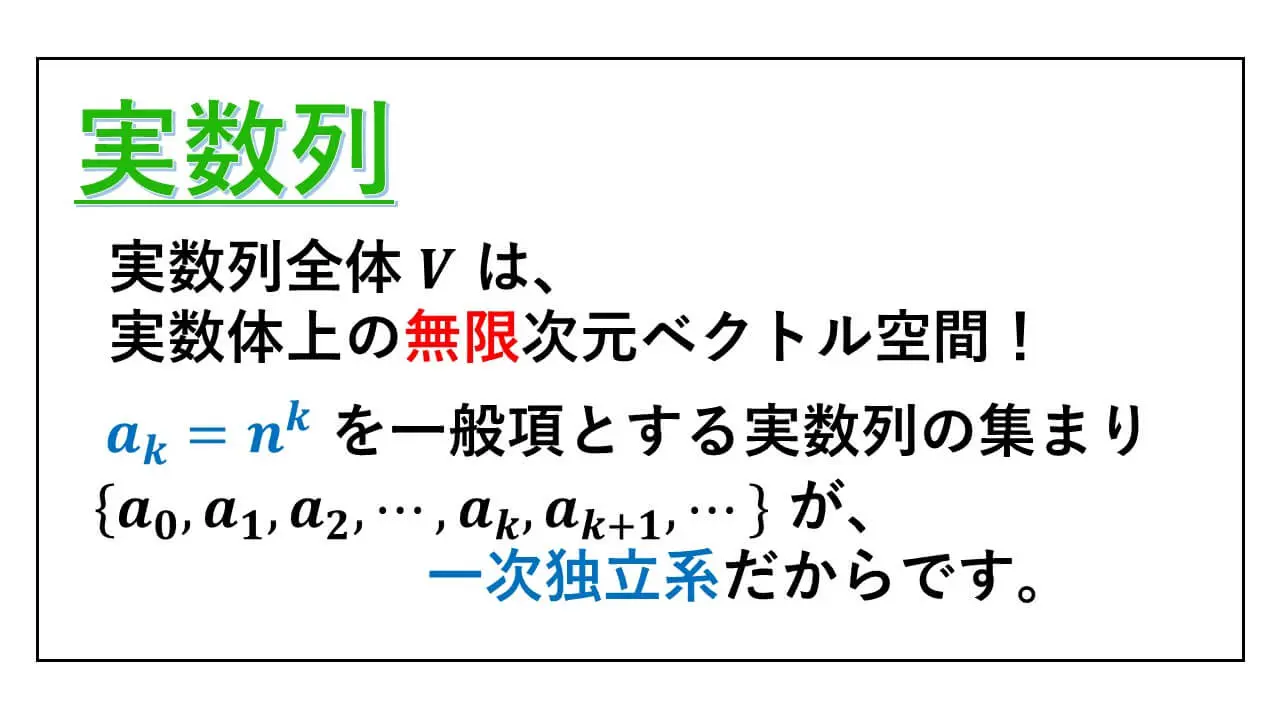
以下では、数列についての極限を扱います。このことは、数列版で証明をすることにします。
高校の数学で、連続の対義語のように離散をという言葉が出てきます。
ただ、これから述べる内容については、あまり対義語のイメージはなく、先ほどの練習問題と同じような要領で議論をすることができます。
定義域が自然数全体である実数値関数のことを実数列といいます。つまり、自然数に対して実数を対応させるわけです。
定義域が、自然数全体だと、離散的になるので、イプシロンエヌ法を使って極限の内容を扱います。
イプシロンエヌ法の練習へ
【数列の収束の定義】
数列{a(n)}が実数aに収束するとは、次を満たすことである。
任意の正の実数 ε (ε>0) に対して、
ある自然数 N が存在し、
n ≧ N ならば、|a(n) - n| < ε となる。
注意点は、この自然数 N は、与えられた ε に応じて定まる自然数ということです。
イプシロン-エヌ論法を使うときにも、イプシロンに対して、どのように N を設定したのかを書いておくことが大切になります。
なお、数列は、自然数全体を定義域とする関数なので、n に対応する値を強調するために an ではなく a(n) と、このブログ記事では書いています。
【練習問題】
数列 {a(n)} と {c(n)} が、ともに実数 a に収束しているとします。そして、数列 {b(n)} について、どの自然数 n に対しても、a(n) ≦ b(n) ≦ c(n) となっていたとします。
このとき、数列 {b(n)} は a に収束することを示してください。
はさみうちの原理です。イプシロンエヌ法の練習として、結論を導きます。
<答案例>
任意に正の実数 ε が与えられたとします。
数列 {a(n)} と {c(n)} は実数 a に収束するので、次のような自然数 N1, N2 が存在します。
n > N1 ならば、|a(n) - a| < ε … ①
n > N2 ならば、|c(n) - a| < ε … ②
①の結論は、ε - a < a(n) < ε + a ということです。
②についても、ε - a < c(n) < ε + a ということです。
ここで、N = max{N1, N2} とおくことにします。そうすると、N よりも大きいどんな自然数 n についても、①と②の仮定が両方とも満たされることになります。
また、この練習問題の仮定より、どんな自然数 n に対しても、a(n) ≦ b(n) ≦ c(n) でした。
そのため、n > N を満たす任意の自然数 n に対して、
ε - a < a(n) ≦ b(n) ≦ c(n)
かつ c(n) < ε + a
よって、ε - a < b(n) < ε + a
すなわち、|b(n) - a| < εが示せました。
ゆえに、イプシロンエヌ法より、数列 {b(n)} が実数 a に収束することが証明できました。【証明完了】
今回のイプシロンエヌ法の証明のように、「max-min」の記号は微分積分の分野でよく使われます。
代数学の基本定理の証明でも、max を定めて関数の連続性を議論しています。
高校の数学で結果を知っているけれども、厳密な証明を大学でするときに、複雑な証明になりますが、大切な根本理論となります。
練習問題2
【練習問題2】
数列 {a(n)} が実数 a に収束し、数列 {b(n)} が実数 b に収束するとします。
このとき、数列 {a(n) + b(n)} は実数 a + b に収束します。
<証明>
任意に正の実数 ε が与えられたとします。
数列 {a(n)} が実数 a に収束するので、ある自然数 N1 が存在して、n ≧ N1 ならば、次が成立します。
|a(n) - a| < ε/2 … (1)
-ε/2 < a(n)-a < ε/2 … (1′)
また、数列 {b(n)} が実数 b に収束するので、
ある自然数 N1 が存在して、n ≧ N1 ならば、次が成立します。
|b(n) - b| < ε/2 … (2)
-ε/2 < b(n)-b < ε/2 … (2′)
このとき、N = max{N1, N2} と置くことにします。
この自然数 N 以上の自然数 n について、(1) と (2) がともに成立します。そのため、(1′) と (2′) もともに成立しています。
よって、(1′) + (2′) より
ε/2 < a(n) + b(n) - (a + b) < ε/2 となります。
すなわち、|(a(n)+b(n))-(a + b)| < ε【証明完了】
イプシロンエヌ法の書き換えへ
それでは、ここからの後半で、イプシロンエヌ法の書き換えについて説明をします。
数学では、必要十分条件どおしで書き換えをすることができます。
イプシロンデルタ論法とよく似たイプシロンエヌ法について、たまに出てくる内容になります。
次の2つの内容 (★) と (☆) は同値(必要十分条件)になります。
書き換え ; 其の一
数列a(n)と実数aについて、
「任意の正の実数εに対して、ある自然数Nが存在し、n ≧ N ならば、
|a(n) - a| < εとなる」(★)
数列a(n)と実数aについて、
「任意の正の実数εに対して、ある自然数Nが存在し、n ≧ N ならば、
|a(n) - a| ≦ εとなる」(☆)
【証明】
まず(☆)を仮定し、(★) を導きます。
正の実数 ε が与えられたとします。
このとき、仮定(☆)より、
正の実数 ε/2( > 0) に対してある自然数Nが存在し、
n ≧ N ならば、|a(n) - a| ≦ ε/2
ε/2 < ε だから、|a(n) - a| < ε
すなわち、与えられたε > 0に対して、自然数Nが存在し、
n ≧ N ならば、|a(n) - a| < ε
ということが示せました。
次に (★) を仮定し、(☆) を導きます。
「≦」は「< または =」ということなので、
|a(n) - a| < εを仮定すると、
|a(n) - a| ≦ ε ということになります。
そのため、(★) を仮定するならば、(☆) が成立することになります。
以上より、必要十分条件であることを示せました。【証明完了】
このように、大学数学では、論理や集合の考え方は、よく使われます。
また、次のようなイプシロン-エヌ法の書き換えもあります。
書き換え ; 其の二
数列 {a(n)} が実数 a に収束するとし、k を正の定数とします。このとき、次の2つは必要十分条件になります。
「任意の正の実数εに対して、ある自然数Nが存在し、n ≧ N ならば、
|a(n) - a| < εとなる」(★)
「任意の正の実数εに対して、ある自然数Nが存在し、n ≧ N ならば、
|a(n) - a| < kεとなる」(☆)
【証明】
まず(☆)を仮定し、(★) を導きます。
正の実数εが与えられたとします。
ε/k > 0 に対して、仮定より、ある自然数 N が存在し、n ≧ N ならば、
|a(n) - a| < k × (ε/k) = ε
すなわち、正の実数εに対して、ある自然数Nが存在し、
n ≧ Nならば、|a(n) - a| < εということだから、(★) が示されました。
次に (★) を仮定し、(☆) を導きます。
正の実数 ε が与えられたとします。
k > 0 なので、kε > 0 です。
仮定より、この正の実数 kε に対して、ある自然数 N が存在し、n ≧ Nならば、
|a(n) - a| < kε
すなわち、正の実数 ε が与えられると、その ε に応じて自然数 N が存在し、n ≧ N ならば、
|a(n) - a| < kε となることが示されました。
よって、(☆) が成立します。【証明完了】
今回のブログでは、論理的な証明の記述を書きました。
n 次元のユークリッド空間などについて議論をするときに、このような内容が出てきます。
関連する記事として、距離関数という記事を投稿しています。
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。