ねじれ群 | アーベル群のねじれ部分群で剰余群をつくると、ねじれのない群になることの証明

" ねじれ群 – ねじれ部分群 “について、基本となる内容を解説しています。
ねじれ部分群でコセットを考えると、どうなるのか。二項演算が可換であるということから議論を広げます。
ねじれ元とは、元の位数が有限位数の元のことです。
有限位数の元全体が部分群になること、そしてコセットを考えるとどうなるのかを論理の飛躍なく説明します。
それでは、ねじれ元の定義から説明します。
ねじれ群 :ねじれ元の定義から
群 A をアーベル群(加法群)とします。A の元 x の位数が有限であるときに、x を A のねじれ元といいます。
位数が有限ということは、ある正の自然数 n が存在して nx = 0 となります。
0 ∈ A は、n = 1 の段階で既に 0 なので位数 1 と有限です。そのため、必ずアーベル群には、少なくとも一つはねじれ元が存在するということになります。
そこで、アーベル群 A のすべてのねじれ元を全部集めた部分集合 T を定義することができます。
※ この T はトーションの頭文字をとりました。
それでは、この T が A の部分群になっていることを確認します。
部分群の定義の確認
x, y ∈ T とすると、T の定義から x と y の位数が有限なので、ある正の整数 m と n が存在して、
mx = 0, ny = 0 となります。
よって、
(mn)(x – y)
= n(mx) – m(ny) = 0 – 0 = 0
これは、x – y の位数が有限であることを示しています。
したがって、x – y ∈ T となり、T が部分群であることの必要十分条件が確認できました。【証明完了】
この部分群 T を A のねじれ部分群といいます。
T が全体 A に一致しているときは、A をねじれ群といいます。
このときは、アーベル群 A のすべての元が有限位数ということです。
なお、0 ∈ T なので、どんなアーベル群についても、必ず T は空集合ではないということになります。
ここで、アーベル群の二項演算は可換なので、どんな部分群も正規部分群ということになります。
そのため、コセットを考え、剰余群を定義することができます。
ねじれ群 – ねじれ部分群 :コセットを考えると
T をアーベル群 A のねじれ部分群とします。
T は A の正規部分群なので、コセットを考えて剰余群を定義することができます。
A/T という剰余群についての基本となる定理を証明します。
言葉の注意ですが、アーベル群 A の元について、有限位数の元が零元 0 のみのとき、A はねじれがない群といいます。
【定理1】
T をアーベル群 A のねじれ部分群とする。
このとき、
剰余群 A/T は、ねじれのないアーベル群である。
<証明>
もし a + T ∈ A/T (a ∈ A かつ a は T の元ではない)の位数が有限だったとします。
※ 背理法を用いて、A/T がねじれのない群ということを示します。
a が T の元ではないということから、T の定義より、a の位数は有限位数ではないということになります。
すなわち、ある正の整数 n が存在して、
n(a + T) = 0 + T
これは、(na) + T = 0 + T ということなので、
na = na + 0
∈ {na + x | x ∈ T} = (na) + T
また、n(a + T) = (na) + T であり、
(na) + T = 0 + T なので、
na ∈ (na) + T
= 0 + T = { 0 + x | x ∈ T}
よって、ある y ∈ T が存在して、
na = 0 + y = y ∈ T
na ∈ T より、T の定義から、
na は有限位数なので、ある正の整数 k が存在して、k(na) = 0
これは、(kn)a = k(na) = 0 ということなので、a が位数有限であることを示しています。
しかし、a の位数は有限位数ではなかったので、矛盾です。
よって、A/T の零元 0 + T を除く全ての元について、位数が有限ではないということが示せました。
つまり、A/T はねじれのない群です。【証明完了】
この【定理1】から、ねじれ部分群 T について A/T を考えると、ねじれ元を分断できることが分かりました。
さらに、ねじれのないアーベル群について確実に成立する定理を考えます。
ねじれがないとき
さきほど、A/T がねじれのない群ということを示しました。
さらに議論を進めるために、一つ定理を準備します。
【定理2】
ねじれがない有限生成アーベル群 A は、有限階数の自由アーベル群である。
<証明>
x1, … , xn という有限個の元で A が生成されていたとします。
これら n 個の元が一次独立だと、示したい結論が導けたことになります。そこで、これらが一次従属であるとして矛盾を導きます。
x1, … , xn から元を選び、一次独立となる個数が最大となるときを考えます。
そして、それらを {y1, … , yk} とします。
{y1, … , yk} という k 個(k < n) で生成される A の部分群を H とします。
つまり、H = <y1, … , yk>
この H は、{y1, … , yk} を基底とする自由アーベル群です。
今、x1, … , xn が一次従属という仮定の下で議論をしているので、H は A に一致していません。
x1, … , xn について、{y1, … , yk} に使われなかった残りを、zk+1, … , zn と置きます。
k < i ≦ n である自然数 i に対して、一次従属であることから、
m1y1 + … + mkyk + mizi = 0 を満たす正の整数 mi が存在します。
※ もし ni = 0 だとすると、y1 から yk が一次独立であることから、m1 から mk がすべて 0 となり、一次従属ということに反してしまいます。
今、mizi ∈ <y1, … , yk> (i は k + 1 以上 n 以下の自然数)となっています。
y1, … , yk の一次結合で表された mixi たちの整数部分 mk+1, … , mn を固定します。
そして、
m = mk+1×…×mn と置きます。
各 mi > 0 より、m > 0 となっています。
ここで、f : A → H を、a ∈ A に対して、
f(x) = ma と定義します。
a, b ∈ A に対して、
f(a + b) = m(a + b)
= (ma) + (mb) = f(a) + f(b) なので、f は準同型写像になっています。
A がねじれのない群ということから、f が単射ということが導かれます。
ねじれなしの仮定の効果
t ∈ ker f とします。
このとき、mt = f(t) = 0 となっています。
これは、t の位数が有限ということを表しています。
仮定より、A にはねじれがないことから、零元を除く全ての A の元の位数は有限ではありません。
そのため、t は A の零元 0 ということになります。
ゆえに、ker f = {0} となります。
群準同型定理から、
A/ker f は Im f と群として同型ですが、
ker f = {0} なので、
A と A/ker f が同型ともなっています。
よって、A と Im f は群として同型です。
ここで、Im f は有限階数の自由アーベル群 H の部分群です。
自由アーベル群という以前に書いたブログ記事に証明を書いているのですが、有限階数の自由アーベル群の部分群も有限階数の自由アーベル群となります。
そのため、Im f は有限階数の自由アーベル群です。
ゆえに、A は Im f と群として同型なので、A も有限階数の自由アーベル群ということになります。【証明完了】
ここまでで証明をした【定理1】と【定理2】を合わせると、次の定理が得られます。
ねじれ群 :コセットを利用して分解
【定理3】
A を有限生成アーベル群とし、T を A のねじれ部分群とする。
このとき、A は T と A/T の外部直和に同型である。
<証明>
記号ですが、A/T の元 x + T のことを x’ と表すことにします。
【定理1】より、A/T はねじれがない有限生成アーベル群です。そのため、【定理2】より、有限階数の自由アーベル群となっています。
{a1', … , an'} を A/T の基底とします。
そして、f : A → A/T を自然な全射準同型写像とします。
すなわち、a ∈ A に対して、
f(a) = a’ = a + T です。
ここで、f が全射であることから、A/T の基底を構成する各元 ai' について、
f(ai) = ai' となる ai ∈ A となっています。
※ ai' ≠ 0’ なので、ai の元の位数は有限ではありません。
今、A/T の代表元を a1, … , an に固定します。
すると、{a1', … , an'} が基底なので、
g : A/T → A を
g(z1a1'+…+znan')
= z1a1+…+znan(各 zi は整数)と定義することができます。
※ 基底の取り方に依存する写像 g です。
合成写像 fg は A/T から A/T への恒等写像となっています。
このことから、g は単射ということになります。
実際、x’, y’ ∈ A/T に対して、
g(x’) = g(y’) とし、これらを f で移すと、
(fg)(x’) = (fg)(y’)
fg が恒等的なので、x’ = y’ となり、g が単射ということになります。
そのため、Im g = g(A/T) は A/T と群として同型になっています。
※ Im g を B と置きます。
{a1, … , an} は B を生成していますが、全体 A を生成しているかは定かではありません。
しかし、A が有限生成という仮定から、有限個の元を補充すると、A の生成系とすることができます。
{a1, … , an, b1, … , bi} を A の生成元とします。
すると、A の任意の元 x はこれらの一次結合で表され、b1 + T, … , bi + T が 、
{a1', … , an'} という A/T の基底の一次結合で表されるので、次のようになります。
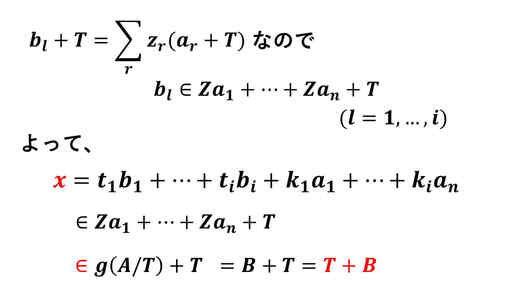
これは、A = T + B ということを示しています。
さらに、x ∈ T ∩ B とすると、x ∈ B だから、
ある a + T ∈ A/T が存在して、
x = g(a + T) … (1)
x ∈ T だから、f(x) = 0 + T なので、
0 + T = f(x)
= fg(a + T) = a + T
よって、
g(a + T) = g(0 + T) = 0
(1) より、x = g(a + T) = 0
したがって、T ∩ B = {0}
これは、A = T + B が内部直和ということを示しています。
よって、B が A/T と群として同型だったので、
A は T と A/T の外部直和と群として同型になります。【証明終了】
さらに、T が有限群だということが分かります。
T の位数が有限な理由
有限生成アーベル群 A のねじれ部分群 T は、位数が有限な有限群ということまで決定できます。
今、証明した定理から、A は T と A/T の外直和(外直積)と群として同型です。
A から T と A/T の外直積への群同型写像を Ψ とします。
そして、 T × A/T の元 (t, a + T) に対して、
t ∈ T を対応させるという射影を p とします。
Ψ と p で写像を合成すると、
A から T × A/T を経由して T への群準同型写像となります。
よって、p(Ψ(A)) = T となります。
A が有限生成なアーベル群だったので、
p(Ψ(A)) = T も有限生成です。
そして、T のどの元の位数も有限というねじれ部分群の定義から、位数 | T | が有限と結論づけられます。
有限個の生成元の元の位数が有限なので、生成されている集合 T は、有限個の元となっているということです。
このねじれ群 T は有限生成アーベル群のねじれ群です。そのため、A が有限生成ということと全射準同型像の関係から、T が有限群ということを導けました。
今回の記事では、直観的に明らかそうな内容を厳密に証明をしました。
外直積と内直積(直和)については、リンク先の関連記事で、基本となる内容を解説しています。
今回のブログ記事の内容から、有限生成のアーベル群が有限階数の自由アーベル群とねじれ群の直和に分解することが分かりました。
このねじれ群 T についての構造を分析したものが、有名な有限生成アーベル群の基本定理となります。
実は、有限生成アーベル群のねじれ部分群は、
アーベルp群の直和に分解しています。
この内容まで押さえると、有限生成アーベル群の構造がかなり見えてきます。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。