微分作用素 d/dx | そんなに難しくない計算で微分方程式や線形性に親しもう!

微分作用素 d/dx を数学IIで学習する計算を中心にして、大学で扱う内容を具体的に解説しています。
微分方程式も、計算がシンプルだと学習し始めに取り組みやすいかと思います。
また、微分作用素と線形性についても具体的な例で様子をみると分かりやすいです。
線形ではない微分作用素もありますが、線形なものを行列でも表しています。
微分作用素 d/dx は x を変数とする関数を 1 回微分するという操作を表します。このブログでは、他に高校の数学II で学習する不定積分も使います。
x で不定積分されてできた関数を x で微分すると、もとの積分する前の関数に戻るという「微分積分学の基本定理」に注目して、微分方程式の内容を解説しています。
微分作用素の記号に慣れるための練習として、シンプルな微分方程式を扱い、その後で、微分作用素と線形代数の内容を合わせたようなことについて述べます。
微分作用素を行列で表すということも後半で述べています。
微分作用素 :微分方程式と不定積分
高校の数学IIで「不定積分」を学習しています。たとえば、次のような計算です。また、x で不定積分をして得られた関数を x で微分すると、もとに戻ることも学習しています。
∫ 4x dx = 2x2 + C(ただし、C は積分定数)
一方、x で微分すると、
d/dx (2x2 + C) = 4x
高校数学2で学習するくらいの不定積分と微分についての内容を使って、微分方程式を扱ってみます。
微分方程式を解く
【練習 1】
f'(x) = 4x
この等式を満たす関数 f(x) は何でしょうか。
等式の意味を考えると、x で微分すると 4x となる関数が何かということです。
先ほどの不定積分についての内容から、x で 1 回微分すると 4x となる関数は、
f(x) = 2x2 + C ( C は積分定数 ) と分かっています。
※ この f'(x) という 1 次導関数は、f(x) に微分作用素 d/dx を 1 回だけ作用させてできた関数です。他の導関数の表し方として f(1)(x) と表すこともあります。
この関数 2x2 + C のことを微分方程式の解といいます。微分方程式については、解が関数ということになります。中学生のときに扱った方程式だと、方程式の解が実数でしたので、解が関数ということに注意です。
1 回微分された導関数を使った、この方程式を微分方程式といいます。
この微分方程式だと、1 次導関数しか現れていませんが、2 次導関数が使われているときもあります。そのときは、2 階微分方程式といいます。
一般に、最も多く微分された導関数が n 次導関数である微分方程式を n 階微分方程式といいます。
【練習2】
f'(x) = ex – e-x
ここで、ex の底 e はネイピア数です。
ex を x で不定積分すると、
その値は ex + C1 です。
そして e-x を x で不定積分すると、
その値は -e-x + C2 となります。
よって、微分方程式の解は 、
「 f(x) = ex + e-x + C 」 となります。
※ C は積分定数です。
定数どおしの和は定数なので、まとめて C を積分定数と表しました。
微分作用素に親しむためにも
【練習 3】
f(2)(x) = -9.8
2 次導関数が使われているので、2 階微分方程式です。この解となる関数 f(x) を求めます。
※ この f(2)(x) という 2 次導関数は、f に まず微分作用素 d/dx を 1 回作用させた後、さらに d/dx を作用させてできた関数です。
f(2)(x) を x で積分すると、
– 9.8 x + C1 なので、
f'(x) = f(1)(x) = -9.8x + C1
さらに x で積分すると、
f(x) = – 4.9x2 + C1x + C2
(ここで、C1 と C2 は積分定数です。)
これで解が求まりました。微分方程式は、数学や物理でよく使われます!
次の練習問題を通して、このブログでの記号の使い方について触れます。
【練習4】
y × y’ = -x
この微分方程式を解きます。
y × dy/dx = -x より、
x について両辺を積分すると、
∫ (y × dy/dx) dx = ∫ (-x) dx
すなわち∫ y dy = ∫ (-x) dx
よって、y2/2 = -x2/2 + C0
(ただし、C0 は積分定数)
※ 記号の注意点として、d/dx は x で 1 回微分するという微分作用素ですが、dy/dx は 1 次導関数です。よく似た記号ですが、表している意味が異なります。
両辺に 2 を掛けると、y2 = -x2 + 2C0
2C0 を C と置くと、C は定数です。
よって、y2 = -x2 + C
これで、微分方程式が解けました。
【注意点】
定数 C は一般にどういった値であるか不明です。
しかし、一つでも曲線 y2 = -x2 + C 上にある点の座標が分かれば、方程式に x 座標と y 座標の値を代入することで、定数 C の値を求めることができます。
<C の値が分かる例>
もし点 (2, 2) が、曲線 y2 = – x2 + C 上にあったとします。
このときに、曲線の方程式に x = 2, y = 2 を代入すると、4 = -4 + C となります。
これより、 C = 8 と定数の値が求まりました。
次に微分作用素について説明します。
微分作用素 :線形性を考えられるシンプルな状況
ここからは、複素数を係数とする n 次以下の多項式全体を V(n) と表すことにします。
この自然数 n という一般的な表し方が重たく感じるかもしれませんので、n = 2 と 2 次以下の複素係数の多項式全体で議論を進めます。
f(x), g(x) ∈ V(2) という複素数を係数とする 2 次以下の多項式どおしで、多項式の加法を計算します。
すると、f(x) + g(x) も 2 次以下の複素数を係数とする多項式なので、V(2) の元(要素)ということになります。
また、複素数 c からのスカラー倍ですが、f(x) ∈ V(2) に対して、どの係数も一斉に c 倍するということで定義します。
単純なスカラー倍の例ですと、虚数単位 i から
f(x) = 2x2 + 5x + 4 へのスカラー倍は、
if(x) = 2ix2 + 5ix + 4i となります。
どの f(x) の係数も複素数 i で一斉に i 倍されています。
一般に複素数 c からのスカラー倍だと、
cf(x) = 2cx2 + 5cx + 4c です。
if(x) も cf(x) も、係数がすべて複素数である 2 次以下の多項式なので V(2) の元です。
この加法とスカラー倍について、V(2) は複素数体 C 上のベクトル空間となっています。
実はベクトル空間には基底が存在するということが一般論で示されているのですが、V(2) の基底は具体的に分かっています。
{x2, x, 1} が基底です。
この 3 個の多項式たちが V(2) の基底となっています。
3 個の元で基底が構成されているので、V(2) は複素数体上の 3 次元ベクトル空間です。
微分作用素を線形写像として考える
f(x) ∈ V(2) を x について 1 回微分するということを微分作用素 d/dx を使って表します。
d/dx(f) が f'(x) のことです。
複素係数の 2 次以下の多項式を 1 回微分しても、複素係数の 2 次以下の多項式という条件に当てはまるので、d/dx(f) ∈ V(2) です。
したがって、d/dx を V(2) から V(2) への写像と考えることができます。しかも、次の二つの性質が成立しています。
(1)V(2) における和を保存する
f(x), g(x) ∈ V(2) に対して、
d/dx(f+g) = d/dx(f)+d/dx(g)…(1)
これは、先に多項式どおしの加法を計算したものを微分することと、先にそれぞれを微分しておいてから加法を計算することが同じ結果の多項式ということを意味しています。
(2) V(2) におけるスカラー倍を保存する
複素数 c と f(x) ∈ V(2) に対して、
d/dx(cf) = c d/dx(f)…(2)
これら (1) と (2) をともに満たすとき、線形写像となっています。
写像についての記号
c という複素数に対して、V(2) から V(2) への写像をスカラー倍を用いて表します。
つまり、
f(x) ∈ V(2) に対し、c(f) = cf(x) と表します。
これは c からのスカラー倍そのものですが、この見方をすることで、写像 c が V(2) から V(2) への線形写像と考えることができます。
※ 和の保存とスカラー倍の保存は、多項式の計算から成立します。具体的な確かめは省略します。
ここで、c も d/dx も V(2) → V(2) という線形写像です。
そのため、写像の合成を考えることができます。この合成写像を c・d/dx : V(2) → V(2) と表すことにします。
※ 高校数学III で学習する合成関数のことです。
実は、この合成写像 c・d/dx も (1) と (2) を満たし線形写像になっています。
もう一つ合成写像を考えます。
(d/dx)2 : V(2) → V(2)
これは、d/dx と d/dx の合成です。合成というと難しそうですが、x で 1 回微分した後で、もう一度 x で微分するということです。
上の微分方程式のときに扱った f(2)(x) は、(d/dx)2(f) のことです。
大学の数学で、この記号に悩むこともあるかもしれませんので、具体例を一つ述べておきます。
<具体例>
f(x) = 3x2 + 4x + 5 を (d/dx)2 で移してみます。
d/dx で微分してから、もう一度 d/dx で微分するということですので、定義の通りに計算します。
(d/dx)2(f) = d/dx(d/dx(f))
= d/dx(6x + 4) = 6 です。
すなわち、(d/dx)2(f) = 6 ということが分かりました。
写像の和
k1 と k2 を V(2) から V(2) への線形写像とします。このとき、k1 + k2 を次のように定義します。
V(2) の元 f(x) に対して、
(k1 + k2)(f) = k1(f) + k2(f)
これは、f(x) に対して、f(x) を k1 で移した多項式 k1(f) と k2 で移した多項式 k2(f) で加法を計算した多項式 k1(f) + k2(f) を対応させるという写像です。
この写像 k1 + k2 も (1) と (2) を満たし、線形写像となります。
ここで、3・(d/dx)2 + 4・d/dx という具体例で、様子をみてみます。スカラー倍を写像として考えたものと微分作用素の合成です。
※ 解析学を学習するときに写像の合成「・」の記号は省略されることが多いかと思います。
f(x) = 3x2 + 4x + 5 を写像の和で移すとどのようになるのかを計算します。
まず 4・d/dx(f) を計算します。
その後で、3・(d/dx)2(f) を計算し、加法を計算すると、
4・d/dx(f) = 4(6x + 4) =24x + 16
次は 2 回微分する方です。
3・(d/dx)2(f) = 3・d/dx(6x + 4)
= 3 × 6 = 18
よって、
(3・(d/dx)2 + 4・d/dx)(f)
= 18 + (24x + 16) = 24x + 34
これで、微分作用素どおしの線形和について扱いました。
実は、有限次元の線形代数の一般理論で、基底を構成する元の線形写像の行き先を基底の線形和で表すことができると、線形写像を行列で表すことができます。
そこで、微分作用素 d/dx と (d/dx)2 を行列で表すことをしてみます。
微分作用素 :行列で表す
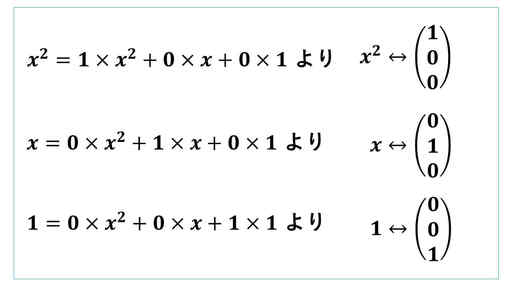
まず、基底を構成する元を列ベクトルに対応させます。
※ 行列表示についての一般論は表現行列というリンク先のブログ記事で解説をしています。
次に基底を構成する元を線形写像 d/dx で移した先を基底の元たちの線形和で表します。
d/dx(x2) = 0 × x2+2 × x+0 × 1
また、
d/dx(x) = 0 × x2+0 × x+1 × 1
d/dx(x2) = 2x を基底の元たちの線形和で表したときのスカラー倍の部分を 1 列目に並べて行列を作ります。行列の成分には、縦にして並べます。
その次に、d/dx(x) = 1 を同じく線形和で表します。今度は行列の 2 列目にスカラー倍の部分を並べます。次の図で、d/dx(1) = 0 から、同じ要領で 3 列目をつくります。

d/dx という線形写像を表す表現行列が求まりました。
この表現行列を使って、微分を行列の計算で表してみます。3x2 + 2x + 5 という多項式を d/dx で微分すると、6x + 2 になります。
まずは、3x2 + 2x + 5 に対応する列ベクトルを考えます。一番下の式で真ん中にある列ベクトルが対応しています。係数の 3, 2, 5 を縦にして列ベクトルとしています。
この列ベクトルに左から、微分作用素の表現行列を掛けると、行列の乗法の計算結果が、微分した後の多項式に対応します。よって、計算結果の列ベクトルを今度を横に倒して多項式の係数とすると、確かに 6x + 2 になっています。
今度は、(d/dx)2 の表現行列を求めてみます。要領は同じです。
■ (d/dx)2(x2) = 2
■ (d/dx)2(x) = 0
■ (d/dx)2(1) = 0
(d/dx)2(x2) = 0 × x2 + 0 × x + 2 × 1 なので、1列目の 3行 1 列の成分が 2 です。その他は、すべて 0 が並んだ行列になります。

先ほど、3・(d/dx)2 + 4・d/dx という微分作用素の線形和の具体例について述べました。この線形和を表現行列を使って表すことができます。
3・(d/dx)2 なので表現行列に 3 をスカラー倍させ、4・d/dx なので 4 をスカラー倍します。それらの行列について、行列の加法を計算すると、求める表現行列となります。
微分作用素の線形和が、行列の線形和として表すことができます。
3・(d/dx)2 + 4・d/dx(3x2 + 4x + 5) = 24x + 34 ということを先ほど計算して求めました。
これを表現行列を使って計算してみます。行列の計算だとすぐに計算できます。
線形和を行列で計算

3x2 + 4x + 5 に対応する列ベクトルをつくって、表現行列を左から掛けます。
この行列の計算結果が、求める多項式に対応する列ベクトルです。
(1, 2) 成分が 24 で、(1, 3) 成分が 34 なので、対応する多項式が 24x + 34 ということになります。
このように微分作用素を具体的に行列で扱うと、微分作用素の理解と合わせて、線形代数の学習にもなります。
線形写像ではない微分作用素の例
微分作用素が線形写像となっていたので、行列で表示できました。しかし、微分作用素の中には、必ずしも線形写像とならないものがあります。
V(8) を 複素係数の 8 次以下の多項式全体とします。V(8) から V(8) への微分作用素を次のように定めます。
D: V(8) → V(8) を f(x) ∈ V(8) に対して、D(f(x)) = f(x) × f'(x) と定義します。微分が絡んでいますが、この D は線形写像ではありません。
f(x) = x3, g(x) = x2 について、調べてみます。
D(f(x) + g(x)) = D(x3 + x2)
= (x3 + x2) × (x3 + x2)’
= (x3 + x2) × (3x2 + 2x)
= 3x5 + 5x4 + 2x3
一方、
D(f(x)) + D(g(x))
= x3 × (x3)’ + x2 × (x2)’
= 3x5 + 2x3
D(f(x) + g(x)) ≠ D(f(x)) + D(g(x)) なので、線形写像の定義を満たしていません。微分が絡めば、線形写像になるとは必ずしも限らないという例です。
行列で表示できるのは、線形写像であることが前提なので、この D だと行列で表示はしないということになります。
Reflectionという行列についての線形変換の記事も投稿しています。
また、End(V)という記事で、一般的な線形変換の成す環について述べています。
それでは、これで、今回のブログ記事を終了します。
読んで頂き、ありがとうございました。