方べきの定理 – 証明 | 中学で習った知識を使い簡単に導こう!
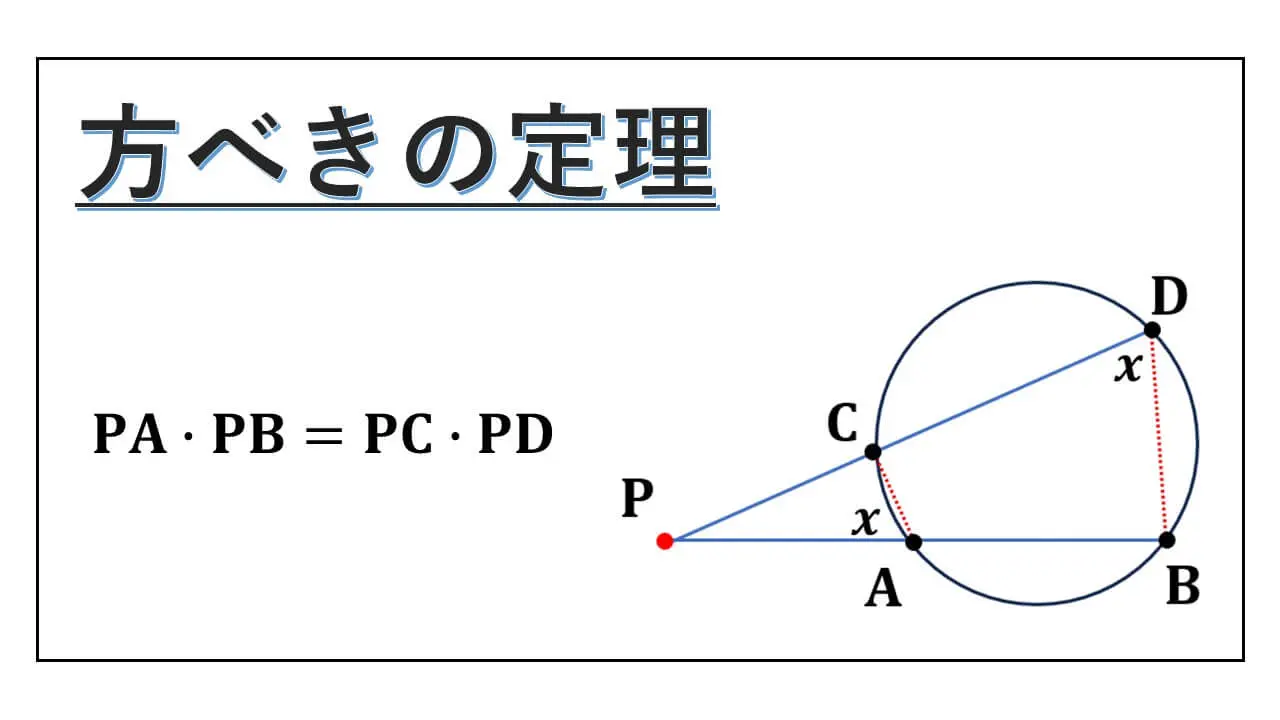
" 方べきの定理 “の証明について解説をしています。
中学の数学で学習した円に内接する四角形についての性質を使い、三角形の相似を利用して結論の等式を導きます。
また、定理の逆についても成立し、たびたび大学受験でも使うことがあります。
どの三角形とどの三角形が相似で、どの辺とどの辺が対応していて、比について内項の積と外項の積が等しいということを丁寧に追うことで、結論を導く流れになります。
方べきの定理には、三つのタイプがあります。
まずは、【1】2本の弦の交点 P についての場合で証明します。
そして、【2】2本の弦の延長の交点が P の場合について証明をします。
【2】の極限状態とでもいうべき【3】の場合も考えられます。
この【3】については、1本が円の接線となっている場合になります。
方べきの定理 :2本の弦から
【定理1】
円の2本の弦AB, CD または、それらの延長の交点を P とする。
このとき、
PA・PB = PC・PD である。
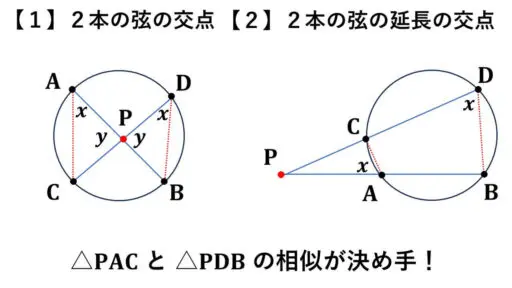
どちらの場合についても、三角形の相似を利用し、相似比から結論の等式を導きます。
<証明>
【1】の場合から示します。
△PAC と △PDB について、
対頂角が等しいため、
∠APC = ∠DPB です。
さらに、
弧CB に対する円周角より
∠PAC = ∠PDB です。
ゆえに、2組の角がそれぞれ等しいので
△PAC ∽ △PDB となっています。
相似な図形の対応する辺の長さの比が等しいため、
PA : PC = PD : PB です。
内項の積と外項の積は等しいため、
PA・PB = PC・PD が示せました。
次に【2】の場合について示します。
△PAC と △PDB について、
共通の角より、
∠APC = ∠DPB です。
また、四角形ABCD が円に内接していることから、
∠BAC と ∠BDC という内角の和は 180°となっています。
※ これを補角の関係といいます。
そのため、
∠PAC = 180°-∠BAC
= 180°-(180°-∠BDC)
= ∠BDC = ∠PDB となっています。
ゆえに、2組の角がそれぞれ等しいので
△PAC ∽ △PDB となっています。
相似な図形の対応する辺の長さの比が等しいため、
PA : PC = PD : PB 【証明完了】
比の相等ということについての扱いが、三角形の相似に関連して重要な証明となりました。
実は、この方べきの定理について、「方べきの定理の逆」も成立します。
逆についても証明を述べておきます。
方べきの定理の逆も真
【定理の逆】
線分AB, CD または、AB の延長と CD の延長の交点を D とする。
そして、PA・PB = PC・PD となっていたとする。
このとき、4点 A, B, C, D は同一の円周上の点である。
<証明>
△PAC と △PDB が相似であることを示します。
仮定より、
PA・PB = PC・PD から、
PA/PC = PD/PB
すなわち、
PA : PC = PD : PB です。
また、共通の角より、
∠APC = ∠PDB です。
よって、
2組の辺の比と、
その間の角がそれぞれ等しいため、
△PAC ∽ △PDB となっています。
相似な三角形の対応する角の大きさは等しいので、
∠PAC = ∠PDB です。
これは、次の二つの場合へと帰結します。
弧CB に対する円周角が等しいので「円周角の定理の逆」から、4点 A, B, C, D は同一の円周上の点。
もしくは「1つの外角が、それと隣り合う内角の対角に等しい」ことから、四角形ABCDが円に内接しているということ。
これで、いずれにせよ、4点 A, B, C, D が同一の円周上の点であることが示せました。【証明完了】
今、示した【2】の場合についてですが、1本が円に接しているという状況についても、方べきの定理が成立します。
【2】の極限状態とでもいうべき【3】について、次で証明を述べることにします。
方べきの定理 :1本が接線のとき
【定理2】
円の外部にある点 P から円に引いた接線の接点を T とする。
そして、P を通る直線と、この円の2つの交点を A, B とする。
このとき、
PA・PB = PT2 となる。
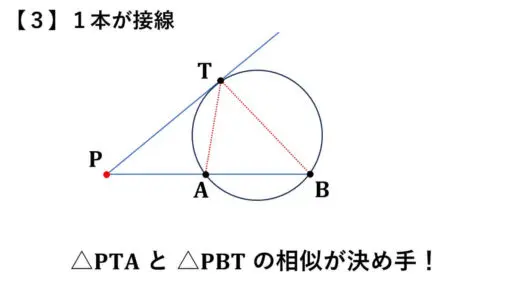
<証明>
△PTA と △PBT が相似であることを示します。
接線PT と弦AT について、
接弦定理より、
∠PTA = ∠PBT です。
また、共通の角より、
∠APT = ∠TPB です。
ゆえに、
2組の角がそれぞれ等しく、
△PTA と △PBT が相似になっています。
よって、対応する辺に長さに関する比を考えると、次のようになります。
PT : PB = PA : PT です。
内項の積と外項の積は等しく、
PA・PB = PT2 【証明完了】
この1本が接線となっている場合についても、方べきの定理の逆が成立します。
逆についての証明を次に述べます。
やはり逆も成立
【定理の逆2】
一直線上にない3点 A, B, T および線分 AB の延長上の点 P が与えられたとする。
さらに、PA・PB = PT2 となっていたとする。
このとき、直線PT は、A, B, T を通る円に接している。
<証明>
△PTA と △PBT において、
共通の角より、
∠APT = ∠TPB です。
さらに、
PA・PB = PT2 より、
PA : PT = PT : PB となっています。
ゆえに、2辺の比と、その間の角がそれぞれ等しいという相似条件を満たしています。
つまり、
△PTA と △PBT は相似な三角形です。
そのため、
対応する角の大きさが等しく、
∠PTA = ∠PBT です。
よって、接弦定理の逆より、
直線PT は、A, B, T を通る円に接しています。【証明完了】
ここまで、方べきの定理の証明について述べてきました。
具体的な数字を用いた練習問題を一つ述べておきます。
【1】,【2】,【3】のいずれの場合かを押さえた上で定理を使うことになります。
練習問題
円の二つの弦の延長が円の外部の点 P で交わっています。
そして、PA = 4, PB = 9,
PC = x, PD = 9+x とします。
このとき、x の値を求めてください。
これは、【2】のタイプとなります。
方べきの定理より、
PA・PB = PC・PD です。
つまり、
4×9 = x(9+x) です。
つまり、x+9x-36 = 0 です。
これより、
(x-3)(x+12) = 0 です。
x は線分の長さなので、
正の実数だから、
x = 3 となります。
二次方程式の解が求める線分の長さとなったときに、線分の長さが正の実数という条件が出てくるので、ここには注意しておくと良いかと思います。
【関連する記事】
・平行線と線分の比
この記事では、メネラウスの定理の証明を解説しています。
・三角形の面積比
この記事では、チェバの定理の証明を解説しています。
・トレミーの定理
円に内接する四角形についての定理です。
図形についての証明は難しいですが、証明に慣れておくと、その後の高校の数学の学習に、その経験が活用できるかと思います。
高校の証明では、場合分けをするときが多いですが、起こり得る場合をすべて考え、導きたい結論を粘り強く考える練習を!
これで、今回の記事を終了します。
読んで頂き、ありがとうございました。