比の相等 | 比が等しいことの定義【三角形の相似も利用する公式の証明】
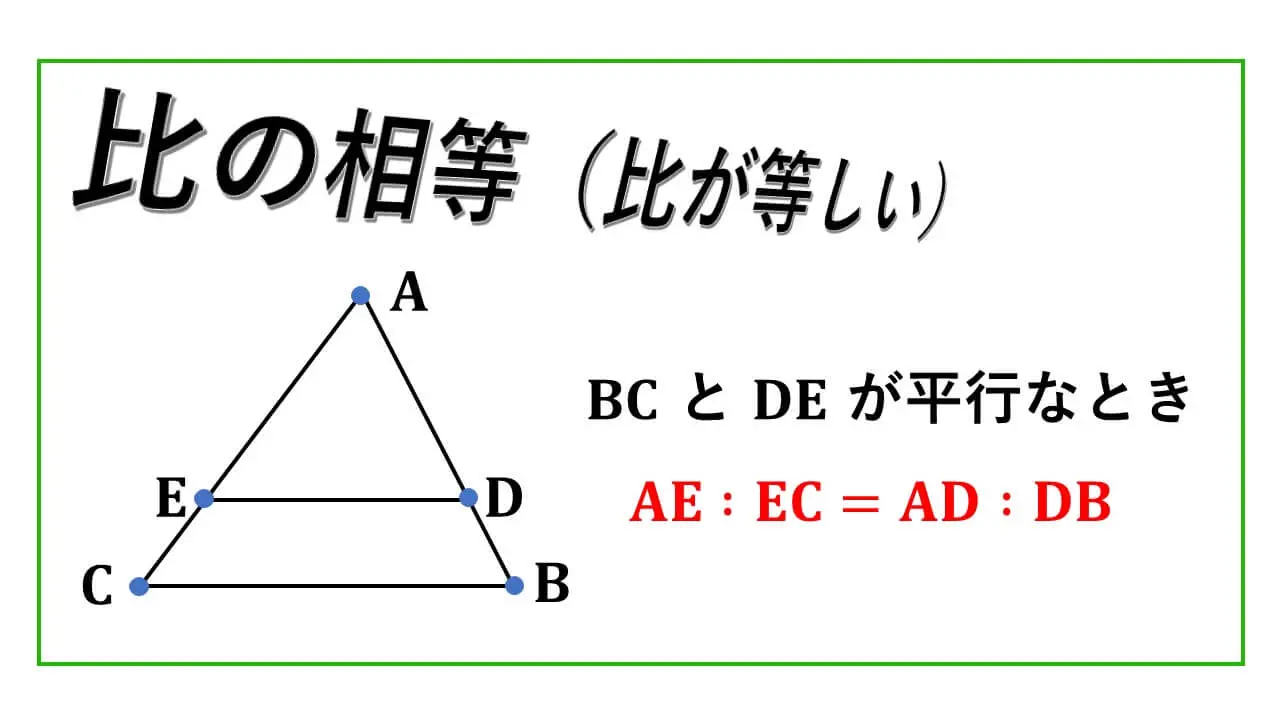
比の相等 （比が等しい）ということの定義を知っておくことは大切になります。
三角形の相似を利用して、対応する辺の比が等しいということから比が等しいということを考えることが多いです。
ただ、三角形の相似からではなく、定義から直接に比が等しいということを計算で示すときもあるので注意です。
この記事では中学の数学で、よく使われる公式を比の相等の定義と三角形の相似の両方を使って証明しています。
まずは、比が等しいということの定義から説明します。
比の相等 :定義を把握することから
【比が等しい定義】
a, b, c, d を正の実数とします。
a : b = c : d とは、
a ÷ b = c ÷ d と定義されています。
a : b について、a ÷ b の値を比の値といいます。
分数で a / b と表されることもあります。
この比の値について、
a ÷ b = c ÷ d であるときに、
a : b = c : d と二つの比をイコールで結びます。
図形的な情報が一切なくても、計算をして割り算の値（分数の値）が等しいときに、定義から二つの比が等しいと結論づけることができます。
直接の計算が困難なとき、三角形の相似を利用して比が等しいということを導くときもあります。
三角形の相似を利用するときの流れをまとめておきます。
相似から比の相等までの流れ
三角形の相似条件を利用して、二つの三角形が相似であることを示します。
△ABC と △DEF が相似ということを先に相似条件を利用して示しておきます。
その次の段階で、相似な三角形の対応する辺の比が等しいということから、二つの辺の長さの比が等しいと結論づけます。
例えば、辺AB と辺DE が対応、辺BC と辺EF が対応しています。
AB ÷ DE と BC ÷ EF の値が、相似な三角形だから同じ値になっています。
そのため、
AB : DE = BC : EF と二つの比が等しいと結論づける流れです。
比が等しいということを示すときに、割り算の値（比の値）を計算して同じだから比が等しいと示す方法と合わせて、三角形の相似を利用して比が等しいことを示すときもあります。
二つの比が等しいことの示し方を押さえておくと、状況に応じて適した方法で比が等しいことを証明するための選択肢が増えます。
それでは、比に関して有名な公式を証明します。
三角形の相似の利用と、直接の計算により定義から比が等しいということを示す方法を、両方とも使い証明を進めます。
どちらの方法も経験できるので、良い練習になるかと思います。
比の相等 :相似の利用と計算から定義の確認
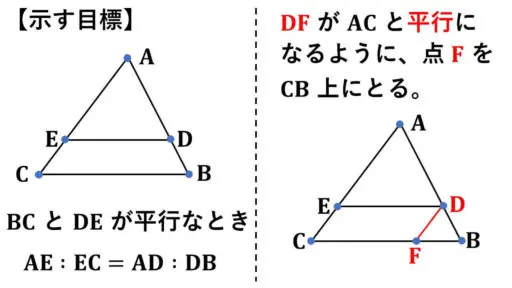
AE : EC と AD : DB が等しいということを証明することを目指します。
右の図のように、AC と平行な直線 DF を補助線として引きます。
まず、仮定から BC と DE が平行なので、四角形ECFD が平行四辺形ということが分かります。
これは、向かい合う二組の辺がそれぞれ平行となっているからです。
平行四辺形の向かい合う辺の長さが等しいことから、
EC = DF …①
この辺の長さについての等式①は後で使います。
ここから、三角形の相似を利用して、
AE : DF = AD : DB となることを示します。
二つを合わせることで、示す目標である二つの比が等しいことを導きます。
△AED と △DFB について
AC と DE が平行であることから、
同位角が等しいため、
∠EAD = ∠FDB です。
また BC と DE が平行だから、
同位角が等しいため、
∠ADE = ∠DBF です。
よって、二組の角がそれぞれ等しいため、
△AED ∽ △DEB です。
相似な三角形の対応する辺の比が等しいことから、
AE : DF = AD : DB …②
この①と②から、
AE : EC と AD : DB が等しいということを導きます。
ここで、直接の計算から定義を確認します。
計算で比の値を確認
今、分かっていること
EC = DF …①
AE : DF = AD : DB …②
②から、二つの比の値が等しいため、
AD ÷ DB = AE ÷ DF …③
①から DF は EC と同じ長さなので、
AE ÷ DF = AE ÷ EC …④
④と③から、
AE ÷ EC = AD ÷ DB です。
比の値が等しいため、二つの比が等しいことの定義から、
AE : EC = AD : DB です。
これで、示したかった二つの比が等しいということを証明することができました。
今回の証明は、高校の数学になっても比について使えるので、証明の流れを振り返っておきます。
証明の振り返り
平行四辺形の性質と二つの相似な三角形を利用して、
EC = DF …①
AE : DF = AD : DB …② を導きました。
この二つは図形的な情報から得られた内容です。
図形的な情報を利用して導いた内容と、計算から導かれる内容を合わせることで、さらに議論を進められるときもあります。
今回の証明では、割られる数が同じであり、割る数の値が等しいから、割り算の計算結果である商が等しいという算数で学習した計算規則を文字で扱いました。
AE ÷ DF = AE ÷ EC を導いたときの考え方です。
割られる数である AE は、どちらの式でも共通です。
そして、割る数 DF と割る数 EC は、平行四辺形の向かい合う辺の長さなので等しいことが①から分かっていました。
割られる数が同じ値で、割る数も同じ値だから、商が等しくなるため、等号で結びました。
そうして AE ÷ DF = AE ÷ EC という等式が得られたわけですが、左辺と右辺の値は比の値です。
ここで、二つの比が等しいということが、割り算の商である比の値が等しいことであるという定義を思い出すと、二つの比が等しいということが分かります。
その結果、
AE : DF = AE : EC ということになります。
また、③から
AD ÷ DB = AE ÷ DF でした。
これも比が等しいということを意味している等式です。
AD : DB = AE : DF ということです。
AE : DF = AE : EC,
AD : DB = AE : DF となっています。
そのため、三つの比が同じということになっています。
特に、
二つの比に焦点を当て、
AE : EC = AD : DB とします。
どちらも AE : DF と等しいということをクッションにして、二つの比が等しいと結論づけました。
比の値を分数で表すと、実数について日頃から使っている内容です。
AE / DF = AE / EC,
AD / DB = AE / DF です。
AE / EC という分数の値は、
AE / DF という分数の値と同じです。
AE / DF という分数の値は、
AD / DB という分数の値と同じです。
そのため、
AE / EC という分数の値は、
AD / DB という分数の値と同じということになります。
※ 専門用語を使うと、実数のイコールについての推移律といいます。
【関連する記事】
今回の記事で、三角形の相似を利用しました。
高校の数学IIの内容ですが、三角形の相似を利用して重要な公式が導かれます。
傾き a と傾き c が 0 でない二つの直線を表す一次関数の式があったとします。
y = ax + b, y = cx + d という直線を表す式です。
この二つの直線が垂直に交わっているとき、
a × c = －1 となります。
二直線が垂直というタイトルの記事で、三角形の相似を使って、この内容を証明しています。
図形からの情報を利用して、等式を導くということは高校の数学でも使われるので、慣れておくと良いかと思います。
最後に、比が等しいということに関する公式を証明しておきます。
比の相等 :外項の積と内項の積
【公式】
a, b, c, d を正の実数とし、
a : b = c : d とする。
このとき、ad = bc
a : b = c : d のイコールの位置を中心に見て、内側の二つの b と c の積が内項の積です。
そして、外側の a と d の積が外項の積です。
a : b = c : d となっているときに、内項の積と外項の積は同じ値となります。
このことを利用して、方程式を作り、未知数の値を決定することがあります。
そんな役に立つ公式ですが、いつでも自信をもって使えるようにするために、証明を押さえておきます。
二つの比が等しいということの定義から導かれる等式になります。
定義に基づいて証明
a : b = c : d の定義より、
a ÷ b = c ÷ d です。
この等式の両辺に bd を掛けて、分母と分子で約分をします。
すると、
ad = bc となります。
定義から、文字式の計算で結論が導かれました。
今、示した外項の積と内項の積が等しくなるということを利用して、未知数を計算で求めてみます。
【練習問題】
2 : 5 = 6 : a となっているとき、実数 x の値を求めてください。
2 : 5 = 6 : a と二つの比が等しいという状況です。
このときに、外項の積と内項の積が同じ値になるということを先ほど示しました。
そのため、
2 × a = 5 × 6 です。
この a についての方程式を解くと、
a = 30 ÷ 2 = 15 となります。
このように、未知数の値を求めるときに、方程式となる根拠として外項の積と内項の積が等しいということを考えるときがあります。
逆も正しい
【逆】
a, b, c, d を正の実数とし、
ad = bc とする。
このとき、
a : b = c : d である。
＜証明＞
a : b と c : d の比の値が等しいということを示すと、定義から結論を得ます。
今、b > 0, d > 0 より、
bd > 0 です。
そのため、bd で両辺を割ることができます。
そのため、仮定より
ad ÷ bd = bc ÷ bd です。
分数の約分をすると、
a ÷ b = c ÷ d です。
これは、a : b の比の値と c : d の比の値が等しいということを意味しています。
よって、
二つの比が等しいことの定義から、
a : b = c : d です。
逆も正しいということが示せたので、高校の数学で学習する必要十分条件ということになります。
高校の数学でも使う内容なので、まとめておきます。
数学では、必要十分条件となっている二つの条件を言い換えることができます。
そのため、状況に適した方で議論を進めることができます。
高校の数学の論理の分野のために、必要十分条件という用語で記述しておきました。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。