酸塩基反応 | アレニウスの定義とブレンステッド・ローリーの定義のちがい

" 酸塩基反応 “について、高校の化学で学習するアレニウスの定義とブレンステッド・ローリーの定義のちがいについて解説をしています。
中学の理科で学習した例を用いてアレニウスの定義から始めます。
その後、酸・塩基(アルカリ性)について、アレニウスの定義では捉えられない酸や塩基。
既に知っていることから学習を始め、理解を広げているので、酸塩基反応のはじめに良い題材かと思います。
まず、酸塩基の学習に必要な用語の内容から述べておきます。
酸塩基反応 :必要な知識の準備
水に溶けたとき、陽イオンと陰イオンに別れる物質のことを電解質といいます。
このプラスイオンとマイナスイオンに別れることを電離といいます。
□+という形が陽イオンで、△-という形が陰イオンです。
例えば、HCl という塩化水素が電解質です。
水に溶けたとき、
H+とCL-に電離します。
電離する電解質について、酸や塩基についての定義を高校の化学で学習します。
中学のときに学習した内容は、アレニウスの定義によって定めた酸と塩基(アルカリ)の定義です。
高校の化学では、ブレンステッド・ローリーの酸塩基の定義も学習します。
定義が異なるので、ちがいを認識しておくことが大切になります。
まずアレニウスの定義から
水に溶けたとき、水素イオンH+を生じる物質を酸とし、水酸化物イオンOH-を生じる物質を塩基とする。
これがアレニウスによる酸と塩基の定義です。
中学のときにアルカリと呼んでいたものを塩基と思えば大丈夫です。
この酸と塩基の定義は中学の理科の化学分野で学習しています。
先ほどの塩化水素は、アレニウスの定義で酸の例となっています。
HCl → H++Cl- と、水に溶けたときに電離します。
H+ を生じたので、アレニウスの定義に当てはまり、酸ということになります。
ちなみに、塩化水素が水に溶けた水溶液のことを塩酸といいます。
今度は塩基の例です。
NaOH → Na++OH- が水酸化ナトリウムの電離です。
NaOH は水酸化物イオンOH-を生じる物質なので塩基ということになります。
これだけだと、中学の理科のときのままなので楽ですが、高校の化学では他の定義が主流になります。
それについて、これから説明をします。
ちょうど高校一年の数学で条件を満たす集合について学習するので、アレニウスの定義に使われている条件とのちがいに注目して、反例に関わる内容を述べています。
ブレンステッド・ローリーの定義で酸塩基
アレニウスの定義に用いられている条件を再び見てみます。
「水に溶けたとき」と、水中の内容に絞られています。
しかし、高校の化学では、気体の化学反応についても酸と塩基の反応を考えることがあります。
そのため、水中だけでなく通用する酸と塩基の定義が望まれるわけです。
例えば、気体の塩化水素と気体のアンモニアが化学反応をしたときに、酸と塩基の化学反応と考えるときがあります。
この場合、水を介していないわけです。
「水に溶けたとき」ときという条件から外れているので、アレニウスの定義では考察することができない状態になっています。
そこで、アレニウスの定義とは異なるブレンステッド・ローリーの酸塩基の定義が活躍します。
気体の塩化水素と気体のアンモニアという中学の理科で既にしっている物質を例に、新しい定義に基づいて酸と塩基を考えてみます。
気体どおしの反応でも使える定義に
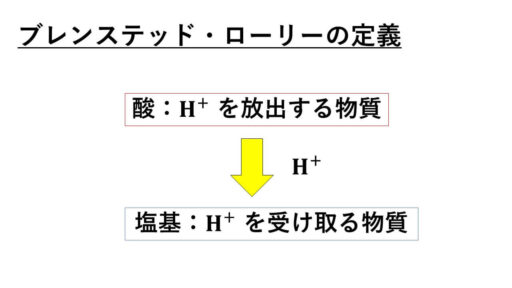
この H+を放出するのか、受け取るのかによって酸と塩基を判断するというわけです。
そのため、OH-が出て来ない反応で酸や塩基を定めることも起こり得ます。
気体のHClと気体のNH3の反応を見てみます。
HCl + NH3 → NH4+ + Cl-
ブレンステッド・ローリーの定義に基づいて、酸と塩基を判断します。
HCl は H+を放出しています。
そして、NH3は H+を受け取って、NH4+になっています。
よって、
H+ を放出したから HCl が酸で、
H+を受け取った NH3が塩基ということになります。
高校の数学でもそうですが、高校の学習では定義に基づいて判断をするということが多くなります。
定義に基づいて判断をすると、小学校以来の常識に合わない学問的な判断となることもあります。
こういうことに慣れながら高校一年から基礎を積み重ねると、大学受験のような難しい問題を解けるようになるかと思います。
水だって酸や塩基に
ブレンステッド・ローリーの定義に基づいて酸か塩基かを判断する練習問題を説明します。
中学の理科から知っている物質ですが、定義に基づいて判断をするので、固定概念通りにならないこともあるので注意です。
【練習問題1】
HCl + H2O → H3O+ + Cl-
この反応において、水H2Oが酸か塩基かを判断してください。
H+を放出する物質が酸で、それを受け取る物質が塩基というのが、ブレンステッド・ローリーの定義に基づいた判断です。
HCl はH+を放出しているので酸です。
そして、H2Oは、
H+を受け取りH3O+になっています。
よって、水H2Oは塩基です。
【練習問題2】
NH3 + H2O → NH4+ + OH-
この反応において、水H2Oが酸か塩基かを判断してください。
H2O はH+を放出して、
OH-になりました。
この H+ を NH3 が受け取り、
NH4+ になっています。
そのため、H+を放出した
水H2Oが酸です。
現代文にも通じる考え方
高校の学習では、1つの科目を学習しながら、他の科目の内容に関連する内容を学習できるときがあります。
そうしたときは、効率よく勉強を進めるチャンスです。
【練習問題1】では、水は塩基でした。
一方、【練習問題2】では、水は酸となっています。
このように、反応する相手によって判断が変化するので、ブレンステッド・ローリーの定義に基づいた酸と塩基の判断は相対的判断となっています。
アレニウスの定義だと、水に溶かして電離したときの状況で判断をするので、いつも一定です。
H+を生じるものが酸、OH-を生じるものが塩基なので、絶対的判断となっています。
国語の現代文を学習するときに、相対と絶対を対比させた読解をすることがあるので、化学の学習を通じても意識しておくと良いかと思います。
ちなみに、返り点という記事では漢文の書き下し文を用いて、数学的な入力と出力に関連する内容を解説しています。
最後に、酸や塩基の強さについて述べておきます。
酸塩基の強さ
高校の化学で、溶解している酸や塩基の強さについて学習します。
この強さを表す数字として、電離度というものがあります。
「溶解している酸(塩基)」に対する「電離している酸(塩基)」の割合が電離度です。
算数で学習した割り算の値です。
この電離度が、ほぼ 1 となっているのが強酸や強塩基です。
「溶解している酸(塩基)」に対する「電離している酸(塩基)」の割合がほとんど 1 ということは、ほぼ百パーセント電離しているということです。
例えば、塩酸HCL だと、
HCl → H++Cl- という電離が水の中でほぼ全てについて起きているということです。
反対に、弱酸や弱塩基だと、ほとんど電離しません。
電離度 0.02 などといったほとんで電離が起きていない状態になります。
酢酸など中学の理科で学習している酸で弱酸の代表的なものがあります。
弱塩基だとアンモニアです。
高校の基礎化学で代表的なものについて問われることがあるので、それらを述べておきます。
強酸と強塩基の例
まず、有名な強酸です。
H2SO4(希硫酸)、
HNO3(硝酸)、
HCl(塩酸)の3つは、すぐに覚えておくと良いかと思います。
他にも高校の化学で出題される強酸はあるのですが、文系の方も含めて、化学を学習し始めた頃に、すぐに覚えておくものに絞って述べておきます。
次は有名な塩基です。
NaOH(水酸化ナトリウム)、
KOH(水酸化カリウム)の2つをまず覚えると良いかと思います。
さらに、
Ba(OH)2(水酸化バリウム)、
Ca(OH)2(水酸化カルシウム)も、よく出題されます。
酸塩基反応という高校の化学についての内容を述べました。
関連する化学についての記事として、アボガドロ定数という記事や原子量-分子量という記事を投稿しています。
さらに、モル濃度-質量モル濃度という基礎の計算に関わる記事も投稿しています。
物理基礎については、運動方程式という記事を投稿しています。
それでは、これで今回の記事を終了します。
読んで頂き、ありがとうございました。