外積 | 定義から、すぐに導ける性質について

2025年3月15日

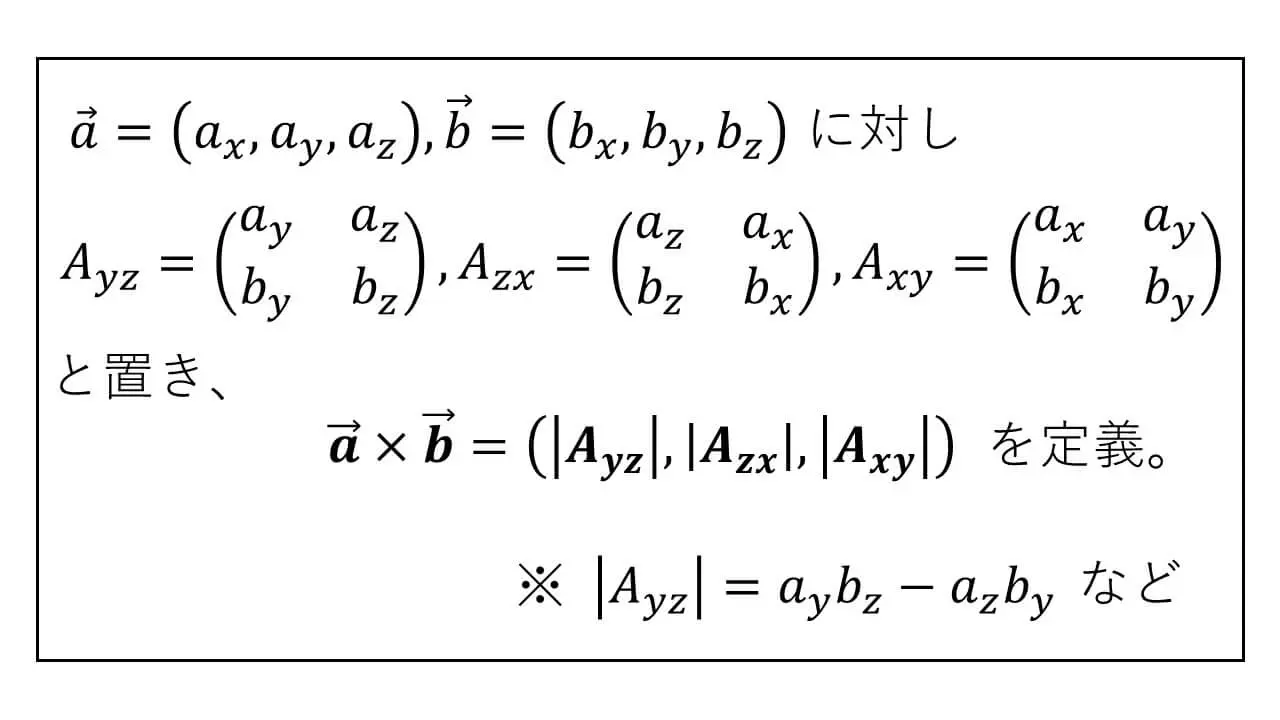
" 外積 “の定義から説明をし、すぐに導ける基本的な性質を証明しています。

高校数学の発展内容になりますが、3次元において２つのベクトルの外積の定義を押さえると、大学受験で役に立つときもあります。

途中の内容を書かないマーク形式の試験で、外積を使って答えを簡単に導ける問題が出題されたこともあります。

また物理でも外積を使ってベクトルを考えることで、理解の幅が広がるときもあります。

そのような外積について、まずは定義から説明します。

規則的に定義されるので、ベクトルの成分について、輪環の順を意識して押さえると習得しやすいかと思います。

※ この記事では、ベクトルの各成分は、すべて実数とします。

外積 : 定義から

a→ = (a_x, a_y, a_z), b→ = (b_x, b_y, b_z) という３次元におけるベクトルが与えられたとします。

このときに、次のようにして、
A_yz, A_zx, A_xy という２行２列の行列を用意します。

(1, 1) 成分 a_y (1, 2) 成分 a_z
(2, 1) 成分 b_y (2, 2) 成分 b_z という２行２列の行列を A_yz と置きます。

左のベクトルが a→ のときに、
１行目の成分が左のベクトルで形成されるという規則です。

A_yz なので、１列目が y 成分、２列目が z 成分という順番です。

輪環の順で、A_zx も作成します。

１行目が左のベクトルの成分で、列については z と x です。

(1, 1) 成分 a_z (1, 2) 成分 a_x
(2, 1) 成分 b_z (2, 2) 成分 b_x となります。

この規則で最後の A_xy を作成します。

(1, 1) 成分 a_x (1, 2) 成分 a_y
(2, 1) 成分 b_x (2, 2) 成分 b_y となります。

行列式を計算する

２行２列の行列の行列式は、学習していなくても、すぐに把握できます。

(1, 1) 成分 a_y (1, 2) 成分 a_z
(2, 1) 成分 b_y (2, 2) 成分 b_z が A_yz でした。

成分の値をたすきに掛け合わせ、差をとります。

a_yb_z－a_zb_y が A_yz の行列式の値です。

(1, 1) 成分・(2, 2) 成分
－(1, 2) 成分・(2, 1) 成分 と計算すると、行列式になります。

|A_yz| という記号で、行列式の値を表します。

すると、
|A_yz| = a_yb_z－a_zb_y ということです。

同様にして、
|A_zx| = a_zb_x－a_xb_z,
|A_xy| = a_xb_y－a_yb_x となります。

３つの行列式の値を計算すると、それらを使って、次のように外積を定義します。

a→×b→ =
(|A_yz|, |A_zx|, |A_xy|) という定義です。

外積をとった後にも空間ベクトルができました。

このように２つの空間ベクトルに対して、新しい空間ベクトルを対応させる二項演算が外積です。

外積をとった後の x 成分の値が |A_yz| という行列式の値です。

y 成分の値が |A_zx| で、
z 成分の値が |A_xy| となっています。

A_yz, A_zx, A_xy という２行２列の行列を規則的に作成できるようになっておくと、行列式は成分をクロスに掛け合わせたものどうしの差なので、外積が求まるわけです。

行列式の値はスカラー量で、それらを各成分に並べたものが外積の計算結果である空間ベクトルというわけです。

※ 内積のときは計算結果がスカラー量でしたが、外積の計算結果はベクトル量になっているので注意です。

では、この定義に基づいて、外積を求める練習をします。

外積を求める具体例

【練習問題】

a→ = (1, 2, 3), b→ = (－2, 3, －5)
という２つのベクトルについて、定義に基づいて外積を計算してください。

＜解説と解答＞

(1, 2, 3) が左のベクトルです。

左のベクトルの成分が、行列の１行目に置かれるという規則でした。

さらに、A_yz, A_zx, A_xy と輪環の順に行列を作成しました。

(|A_yz|, |A_zx|, |A_xy|) という空間ベクトルが、外積の計算結果となるベクトルです。

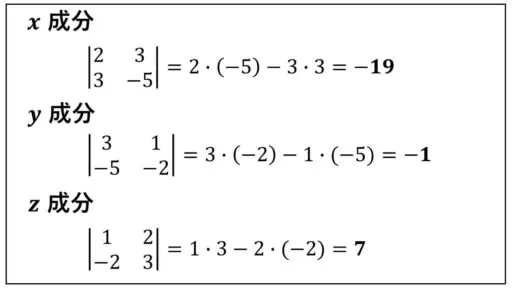
これで、a→×b→ = (－19, －1, 7) と答えが求まりました。

ここで、外積の性質を具体的に見てみます。

外積の後のベクトルは垂直

(－19, －1, 7) という外積の結果のベクトルは、
(1, 2, 3), (－2, 3, －5) という、はじめの２つのベクトルの両方と垂直になっています。

ベクトルが垂直かどうかを確かめるために、内積を計算してみます。

(－19, －1, 7)・(1, 2, 3)
= －19－2+21 = 0 です。

(－19, －1, 7)・(－2, 3, －5)
= 38－3－35 = 9 です。

確かに、はじめの２つのベクトルのどちらとも垂直になっています。

a→×b→ は、
(1, 2, 3), (－2, 3, －5) という１次独立な２つのベクトルによって張られる平面に、垂直な空間ベクトルです。

実は、外積には次の性質があります。

文字を使った一般的な証明は、複雑になるので、先ほどの具体例で事実として述べるに留め、証明は省略します。

次に外積のベキ零性という性質を示します。

自分自身で外積をとると零ベクトルになってしまうという内容です。

外積の基本性質と証明

【外積の性質２】

a→ = (x, y, z) について、
a→×a→ = (0, 0, 0) である。

＜証明＞

a→×a→ = (|A_yz|, |A_zx|, |A_xy|) です。

行列式の値が、どれも 0 になっていることが分かります。

つまり、
|A_yz| = yz－zy = 0,
|A_zx| = zx－xz = 0,
|A_xy| = xy－yx = 0 です。

よって、外積の計算結果が、
(0, 0, 0) です。【証明完了】

外積という二項演算について、一般に交換法則は成立しません。

その代わりに、次の交代性が示されます。

外積の交代性

【外積の性質３】

a→ = (p, q, r), b→ = (x, y, z) とする。

このとき、a→×b→ = －b→×a→ である。

＜証明＞

外積の定義に基づいて計算をします。

a→×b→ =
(qz－ry, rx－pz, py－qx)
・・・①

b×a =
(yr－zq, zp－xr, xq－yp)
= －(qz－ry, rx－pz, py－qx)
・・・②

②を－1 でスカラー倍をすると、①になります。
【証明完了】

通常の実数の掛け算と違って、外積を計算するベクトルの順番を逆にすると、－1 でスカラー倍され向きが反対になります。

最後に外積について、分配法則が成立することを示します。

外積と加法の関係

【外積の性質４】

a→ = (p, q, r), b→ = (x, y, z),
c→ = (x’, y’, z’) とする。

このとき、
a→×(b→+c→) = a→×b→+a→×c→ である。

＜証明＞

まず、
b→+c→ = (x+x’, y+y’, z+z’) ということを用いて、
a→×(b→+c→) の成分をそれぞれ計算します。

【x 成分の値】

q(z + z’) － r(y + y’)
= (qz － ry) + (qz’ － ry’)

【y 成分の値】

r(x + x’) － p(z + z’)
　= (rx － pz) + (rx’ － pz’)

【z 成分の値】

p(y + y’) － q(x + x’)
　= (py － qx) + (py’ － qx’)

ここで、
qz － ry, qz － ry, py － qx は、
それぞれ a×b の x 成分、y 成分、z 成分の値です。

また、
qz’ － ry’, rx’ － pz’, py’ － qx’ は、
それぞれ a×c の x 成分、y 成分、z 成分の値です。

よって、示したい等式が導けました。【証明完了】

他にも基本性質として、外積をとった後のベクトルの大きさについての内容があります。

これについては、平行六面体の体積というnote記事で示しています。

【関連記事】

■ 内積の定義

■ 空間ベクトル

これで、今回の記事を終了します。

読んで頂き、ありがとうございました。